磨光集新探

刘保乾

（西藏自治区组织编制信息管理中心，西藏 拉萨 850000）

文献[1]提出了磨光集的概念，从而得到了自动加强不等式的一种新途径.但文献[1]中的算法要依赖于优秀机器证明软件Bottema[2]，而且当最佳系数不可求时，磨光过程会遇到麻烦.本文以不等式的式商及标准数据为切入点，对磨光集进行了新探讨，提出了稳定集的概念，并编写了应用程序.大量实例表明，文中的算法和程序是实用而有效的.

以下设ΔABC的三边为a，b，c，半周为s，内切圆半径为r，外接圆半径为R，面积为 Δ，中线、角平分线、类似中线和高依次为 ma，mb，mc、wa，wb，wc、ka，kb，kc和 ha，hb，hc，旁切圆半径为ra，rb，rc，用Σ表示循环和.

1 有关概念

1.1 式差，式商

设有不等式

称（2）式为不等式（1）的式商形式.

1.2 参考数据集

不等式（1）是有强弱之分的，但这种强弱是相对的，要有个比较范围.因此，需要定义一个参考数据集.

1.2.1 标准数据

如果一个表达式满足：

i它是一个比值的形式，且量纲为零；

ii它关于它所含的变元的对称性相同；

iii当它的变元满足条件E时，取值为1；

iv它的值不小于1.

则称这个表达式为标准数据，称E为这个标准数据的取等号条件.

例1在ΔABC中，任何一个由三角形常见元素构成的表达式均可用其边长表示出来.现取条件为E＝{b＝c}，则表达式就是一个标准数据，这是因为的量纲为零，且关于边长b，c对称，当b＝c时

例3在ΔABC中，取条件为E＝{a＝b，或者b＝c，或者c＝a}，则表达式就是一个标准数据，这是因为的量纲为零，且关于 a，b，c 对称，由杨学枝、尹华焱的不等式[3]

例5在ΔABC中，取条件为E＝（2a＝b＋c），则表达式就是一个标准数据，这是因为的量纲为零，且关于b，c对称，当 2a＝b＋c时

例2中标准数据的取等号条件包含了例1中标准数据的取等号条件，我们就说这两个数据的取等号条件是兼容的，而例4中的标准数据则不能同它俩兼容，这是因为取等号条件和a＝b＝c无法统一.

1.2.2 参考数据集

由取等号条件兼容的标准数据构成的集合为参考数据集.在一个确定的取等号条件E下，标准数据的全体记为ΩE，或简写为Ω.

由于构造出全体是不可能的，在实际研究中，一般取由具体给出的标准数据构成参考数据集.随着研究的深入，可根据实际需要逐步扩充.

1.2.3 参考数据集的性质

i如果q1∈Ω，q2∈Ω 则

ii不等式的式商构成一个标准数据，其取等号条件与不等式相同.

1.3 加强集，磨光集

1.3.1 加强集

成立，则称不等式

为不等式（1）对qi的加强不等式，称集合为不等式（1）对集合S的加强集.

注意，对加强集中的元素，可在S中继续进行比较，从而得到更强的不等式集，而且这个过程可以一直进行下去，直到在S中找不到一个元素q，使不等式成立，此时称

为不等式（1）在参考数据集S下的最佳加强不等式.所有的最佳加强不等式的式商构成不等式（1）的最佳加强集.

1.3.2 磨光集

可以看出，加强不等式就是以参考数据集中的元素（即标准数据）为单位对不等式进行切割的过程，而且每切割一次，如果剩余的部分还足够，就可以继续切割，直到不能切割为止，最后剩下的部分就是最佳不等式.如果一个参考数据集中的元素，均以其他元素为单位进行切割，剩余的部分再构成新的数据集，如此反复切割，这样形成的数据碎片就会越来越小，直至达到一个不能切割的水平，从而使数据集趋于一个确定的集合.这个过程十分类似于文献[1]定义的磨光集，只不过那里是以式差（横向）的方式磨光的，而这里则是通过式商（纵向）的方式实现磨光的.

1.3.3 稳定集

显然，还可以对磨光集继续进行打磨，并反复进行磨光.

设有参考数据集S，在对S的磨光过程中，如果某次磨光产生的磨光集T满足M（T）＝T，则称T为S的稳定集，用符号W（S）表示，即

可以看出，稳定集本质上就是磨光集，只不过此时集合中的标准数据已经被“磨平”了，无法再进行切割，因此集合中元素的数目就不再变化了.但一个参考数据集是否总有稳定集？这是需要进一步探讨的.

稳定集是磨光过程趋于稳定的产物，到底需要多少次打磨才能稳定，这取决于参考数据集中元素的性状.所以，稳定集从一个侧面反映了参考数据集中各元素之间的制约关系和数量关系.稳定集无疑是很重要的，但许多情况下求稳定集是比较困难的，特别是参考数据集中有太大或太小的元素时，磨光过程中会切割出许多数据碎块，往往会出现死机或运算时间超长的情况.此时可以选用部分数据进行磨光，虽然这是无奈之举，但仍然是很实用而有效的策略.

为了与文献[1]中定义的磨光集相区别，可称本文中的磨光集为商式磨光集，而称文献[1]中定义的磨光集为差式磨光集.

2 算法和程序

由于稳定集是通过磨光集产生的，故磨光集的算法是关键.而磨光集的算法在文献[1]的算法BOTKMGQ中已有详述，所不同的是，在BOTKMGQ中，是通过调用Bottema软件计算最佳系数得到的，而本文中，由于标准数据是以式商的形式出现，这样磨光时，每次只要直接测试数据大小即可，而这可以调用随机数验证程序otf直接实现，故这里不再详述算法.根据最佳加强集、磨光集和稳定集的定义，再结合文献[1]中的算法BOTKMGQ，不难编写相应的程序模块，从而得到相应的新命令，即最佳加强集命令bsset，磨光集命令mgyc以及稳定集命令wdj.这些命令将作为agl2012程序的新功能，出现在以后的各种应用场合.本文程序的运行环境是Intel（R）Core（TM）i5-2450M CPU@2.50GHz，编程语言是Maple15.

3 应用举例

例6在ΔABC中，由数据a，ha，ra构造对称不等式，这些不等式的式商构成一个数据集，试确定这个数据集的稳定集.

解 键入命令：

从而得到一个数据集D，D中的数据满足标准数据的条件，且取等号条件是a＝b＝c，故D构成一个参考数据集，具体数据是：

现求D的稳定集.键入命令：

则显示

上述数字表明，对数据集D进行了3次打磨，最后得到了稳定集，且稳定集中有8个元素，用时204.767s.稳定集中的数据如下

W中的数据对应8个不等式，且这些不等式对参考数据集D来说是最佳的.如有不等式

如果在数据a，ha，ra的基础上再加入r，即将语句改为

则仿上述过程可产生一个有24个元素的数据集D.在执行wdj（D）命令后，经过相当长时间的计算，最后显示出如下数字：

这些数字表明，对数据集D进行了5次打磨最终得到了稳定集，且稳定集中有38个元素，用时约36619.862s.稳定集中的数据此略.

例7为了建立关于ma－r的不等式，且不等式的取等号条件为b＝c，键入命令

可得到一个参考数据集：

在te中，每个标准数据取等号条件均是b＝c.现求te的稳定集.键入命令：

经过46.64s运算后，输出

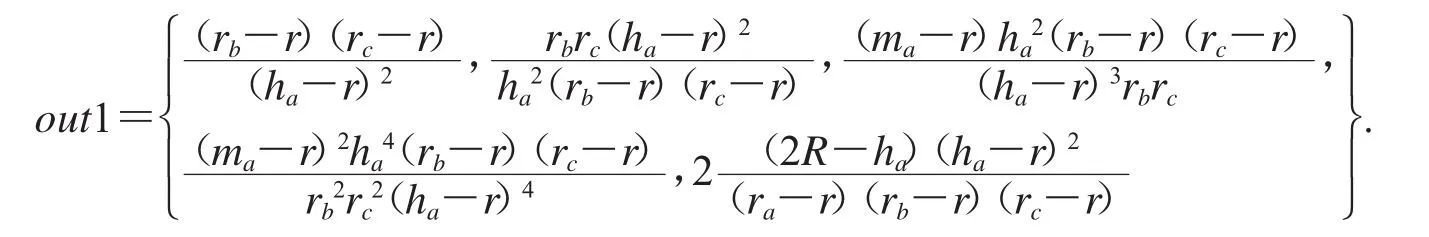
out1就是te的稳定集.在out1中，与ma－r有关的不等式有2个，为

上述得到不等式（10），（11）的过程可以描述为：我们对参考数据集te进行了若干次打磨，最后稳定于out1那种状态——以后无论再打磨多少遍，其中的元素均保持不变.

陈计曾建立关于三角形中线的不等式

不等式（12）取等号的条件是b＝c.由（12）式得标准数据由于不等式（12）较强，那么对于正在打磨的参考数据集te来说，就是一个更小的数据“刀片”.现设想一下，这样的“刀片”放入te中去打磨，将会把参考数据集中的元素切割的更小，从而得到更强的不等式，事实会是如此吗？现用wdj命令进行验证：

加入新的更小的“刀片”后，参考数据集变成

键入命令：

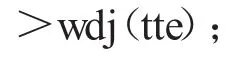
则经过2035.891s运算后，输出

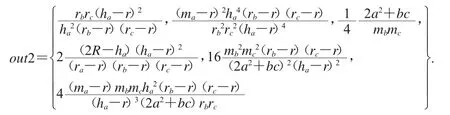
即经过一系列打磨后，得到了稳定集out2.在out2中，有意义的不等式是

不等式（13）反向加强了式（12）.

此时参考数据集变为

键入命令：

则经过16371.962s运算后，输出

注意ttte中只有9个元素，而此时out3中已经有21个元素（限于篇幅，这里省略了部分结果），即当加入“大块头的”标准数据后，经过一系列打磨过程，磨光稳定于21个碎片的状态，即得到稳定集out3.

out3中的每个数据对应一个最佳不等式，而且不少结果是很有意义的，因为它们是关于三角形中线的上界或下界型不等式，这里不再一一列出.

此例说明，在磨光集或稳定集的背景下，不仅强的不等式很有用的，而且平凡的不等式同样也有用，因为，当它们被不同的“刀片”切割时，产生的碎片的价值是不可预料的.这暗示今后发现特殊取等号条件的不等式或更强的不等式的门槛和条件会更低，不等式的来源也更广泛.

例8为了建立关于ΔABC类似中线ka的不等式，且不等式的取等号条件为b＝c或a2＝b2＋c2，键入命令

＞zjbj_otfqdcs（yc，yc，0，0，1，1，1，1，1）；

＞ls:＝glybzjsz（lbqc（gldj（dy），{1}））；#过滤直角三角形时取等号的结果#则可得参考数据集

在ineq中，每个标准数据取等号条件均是b＝c或a2＝b2＋c2，求ineq的稳定集，易发现优美不等式

一般来说，发现上述特殊取等号条件的不等式是十分困难的.

例9在ΔABC中，有Panaitopol不等式

试加强不等式（14）.

解 注意不等式（14）的取等号条件是{a＝b＝c}，这与条件{b＝c}有交集，故可以调用例7中的参考数据集进行加强.求不等式（14）的式商对参考数据集的最佳不等式集，即键入命令：

则输出最佳不等式集

out中的4个数据元素对应不等式（14）的4个加强不等式，这里不再细述.

例103元3次schur不等式是

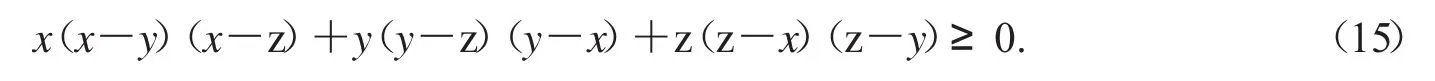
试加强不等式（15）.

解 首先写出不等式（15）的式商.为此，将不等式（15）变为（1）的形式，得

对于不等式（16）的式商，构造一个参考数据集（参考数据集可有多种方法预先给出），再计算稳定集，得到一个由5个数据元素构成的集合，其中第1个元素对应的不等式链是

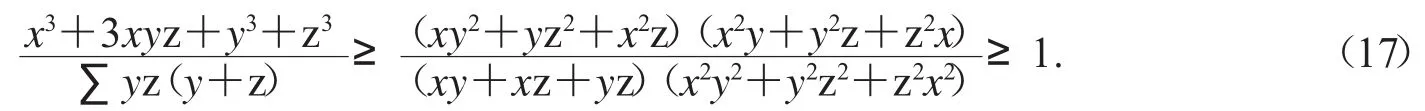
（17）式显然是不等式（15）的加强.其余加强结果限于篇幅，这里不再列出.

4 结语和问题

如果说文献[1]是以式差的方式横向磨光的话，那么本文中的磨光则是以式商的方式纵向磨光的.不论何种磨光方式，其结果都将会导致数据被切割成碎块——发现更强的不等式，而且这两种磨光方式是不可互相取代的.从这种意义上来说，本文是文献[1]有益的补充和发展.事实证明，稳定集将使agl2012程序由批量发现不等式上升为批量发现一些特殊取等号条件不等式，虽然目前的探索只是初步的，但这个途径似乎已经找到了.

稳定集，秩序图[4]和量级[5]，外加不等式自动发现与判定程序agl2012，为系统研究和发现不等式尤其是三角形几何不等式，搭建了基本的思路和框架，绘制了一个清晰的思路.如何补充和完善算法，扩大应用范围，值得进一步研究和探讨.