双重MS-代数的正则理想
赵秀兰,陈丽娟
(1.黄河科技学院数理部,河南 郑州,450063;2.河南工程学院理学院,河南 郑州,450007)
1977年,Joe Berman将布尔代数推广到Ockham代数[1](L;∧,∨,f,0,1),即在有界分配格上赋予一个偶自同态的一元运算f,且
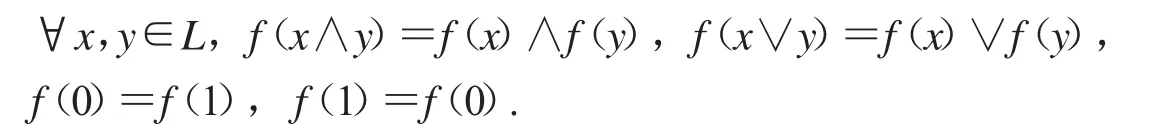
布尔代数、Stone代数、de Morgan代数等是Ockham代数的子代数.作为Stone代数、de Morgan代数的共同抽象,Blyth引入MS代数[1]的概念.对MS代数做更深层次的研究,陆续产生新的扩充MS-代数,例如双重MS-代数,双重半伪补MS-代数等(详细的信息见文献[2-4]).
对序代数结构的研究,常借助理想和滤子,是人们认识序代数-Ockham代数类的结构及同余关系的一个重要工具.文献[5]给出了双重MS-代数正则滤子同余关系的表达式;文献[6-11]以理想与滤子为工具刻画了相关Ockham代数的结构,给出了相应Ockham代数理想和滤子同余关系表达式.本文作为文献[5]的补充,讨论双重MS-代数正则理想与正则滤子的关系,丰富序代数结构的研究.
1 预备知识
定义1.1[1]设(L;∧,∨,0,1)是一个有界分配格,其上赋予一元运算o,且满足条件:
(1)(∀x∈L)x≤xoo;(2)(∀x,y∈L)(x∧y)o=xo∧yo;(3)1o=0.称(L;∧,∨,o,0,1)为 MS-代数.
定义 1.2[1]设(L;∧,∨,o,+,0,1)是一个(2,2,1,0,0)型代数,且满足条件:
(1)(L;∧,∨,o,0,1)是 MS-代数;
(2)(L;∧,∨,+,0,1)是对偶 MS-代数;
(3)(∀x∈L)xoo=xo+,x++=x+o.
称(L;∧,∨,o,+,0,1)为双重 MS-代数.
定义 1.3[12]设(L;∧,∨)是一个格,I是格 L 的子格,若 x,y∈L,y≤x∈I总有 y∈I,称子格I是格L的理想.对偶地,F是格L的子格,若x,y∈L,y≥x∈F总有y∈F,称子格F是格L的滤子.
定义 1.4[5]设(L;∧,∨,o,+,0,1)为双重 MS-代数,F 是 L 的滤子,若 x∈F 总有x+o∈F,则称F是L的正则滤子.
定义 1.5[1]设(L;∧,∨,o,+,0,1)为双重 MS-代数,θ是 L 的一个格同余关系,若
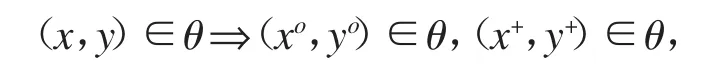
则称θ是L的同余关系.
便于阐述,假定L是双重MS-代数,a,b∈L,F⊆L,用θ(F)和θlat(F)分别表示包含F的最小同余与最小格同余(即由F所生成的主同余和格主同余).符号ConL表示L的全体同余关系构成的集合.
引理 1.1[5]设(L;∧,∨,o,+,0,1)为双重 MS 代数,F 是 L 的正则滤子,则
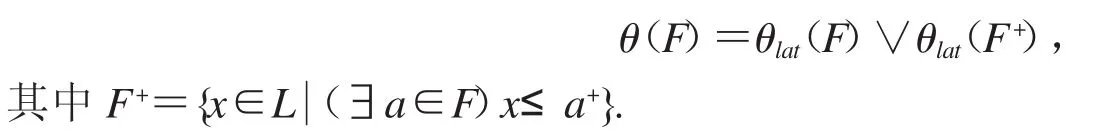
引理 1.2[5]设(L;∧,∨,o,+,0,1)为双重 MS 代数,F 是 L 的正则滤子,则
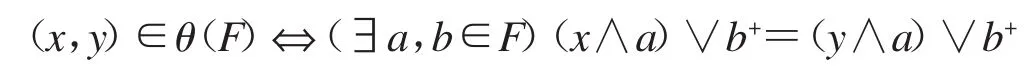
引理 1.3[5]设(L;∧,∨,o,+,0,1)为双重 MS 代数,φ∈ConL,则
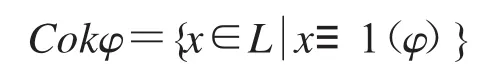
是L的正则滤子,且
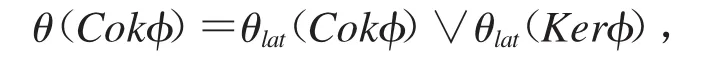
2 主要定理
设(L;∨,∧,o,+,0,1)是双重 MS-代数,I是 L 的理想,若 x∈I总有 xo+∈I,则称 I是L的正则理想.
定理 2.1 设(L;∨,∧,o,+,0,1)是一个双重 MS代数,I是 L 的正则理想,则
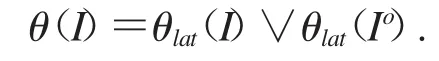
证明 引理1.1的对偶命题.详细证明请参见文献[5,定理1].
以定理2.1为基础,给出θ(I)的另一种形式的刻画.
定理 2.2 设(L;∨,∧,o,+,0,1)是一个双重 MS 代数,I是 L 的正则理想,则
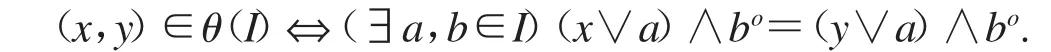
证明 引理1.2的对偶命题.详细证明请参见文献[5,定理2].
推论 2.1 设(L;∨,∧,o,+,0,1)是一个双重 MS-代数,φ∈ConL,则 kerφ 是 L 的正则理想且
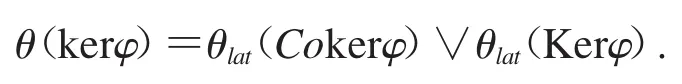
证明 引理1.3的对偶命题.详细证明请参见文献[5,定理3].
设L是双重MS-代数,对于L的正则滤子F和正则理想I,记集合
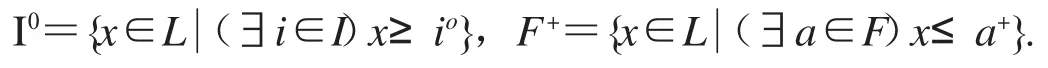
显然,I0,F+分别为L的滤子和理想.下面,进一步探讨正则滤子F和正则理想I的关系.
定理 2.3 设(L;∨,∧,o,+,0,1)是一个双重 MS-代数,又设 I及 F 分别是 L 的正则理想与正则滤子,则
(1)I0是L的正则滤子;(2)F+是L的正则理想.
证明 (1)显然,I0为L的滤子.设x∈I0,则∃i∈I,使得x≥io.结合双重MS代数的运算性质,x+o≥io+o=(io+)o.由正则理想的定义知,io+∈I.又有 I0的定义得,x+o∈I0,所以I0是L的正则滤子.
(2)显然,F+为 L 的理想.设 x∈F+,则∃a∈F 且 a+o∈F,使得 x≤a+.结合双重 MS代数的运算性质,xo+≤a+o+=(a+o)+.从而 xo+∈F+,所以 F+是 L 的正则理想.
设(L;∨,∧,o,+,0,1)是一个双重 MS-代数,又设 I及 F 分别是 L 的正则理想与正则滤子,按照定理2.3定义的Io,F+,正则理想I与正则滤子F之间建立下列等式关系.
定理 2.4 (1)Io+=I;(2)F+o=F.
证明(1)由定理 2.3 知,Io+为 L 的正则理想.设 x∈Io+,则∃i∈Io,j∈I,使得 x≤i+,i≥jo.从而 x≤jo+.又因 I是 L 的正则理想,则 jo+∈I,于是 x∈I,因此 Io+⊆I.
另一方面,设 x∈I,由正则理想的定义知,xo+∈I.由 I0定义得,xo∈Io,易得 xo+∈Io+,又因 x≤xoo=xo+,所以 x∈Io+,故 I⊆Io+.
综上所述,Io+=I
(2)由定理 2.3 知,F+o为 L 的正则滤子.设 x∈F+o,则∃i∈F+,j∈F,使得 x≥io,i≤j+.从而 x≥j+o.又因 j+o∈F,于是 x∈F,因此 F+o⊆F.
另一方面,设 x∈F,则 x+o∈F.又因 x≥x+o=x++,所以 x∈F+o,故 F⊆F+o.
综上所述,F+o=F.
设L是双重MS-代数,记I(L),F(L)分别表示L的理想和滤子构成的集合,NI(L),NF(L)分别表示L的正则理想和正则滤子构成的集合,则有下列定理.
定理 2.5 设(L;∨,∧,o,+,0,1)是一个双重 MS-代数,
(1)NI(L)是I(L)的子格;
(2)NF(L)是 F(L)的子格.
证明(1)令I1,I2∈NI(L),下证I1∧I2,I1∨I2∈NI(L).
设x∈I1∧I2,则x∈I1,x∈I2.又因I1,I2∈NI(L),故xo+∈I1且xo+∈I2.故xo+∈I1∧I2,所以,I1∧I2∈NI(L)
再令 x∈I1∨I2,由文献[12]知,存在 i1∈I1,i2∈I2,使得 x≤i1∨i2.又由文献[1]中双重MS-代数的运算性质得,又因因此xo+∈I1∨I2,所以I1∨I2∈NI(L)定理得证.
(2)和(1)类似的方法,可证 NF(L)是 F(L)的子格.
对于L的正则理想集NI(L)和正则滤子集NF(L)之间满足下列定理.
定理2.6NI(L)≅NF(L)
证明定义映射α:NI(L)→NF(L)和映射β:NF(L)→NI(L),使得
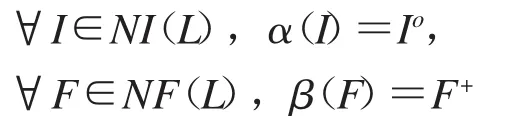
设I1,I2∈NI(L),F1,F2∈NF(L),由定理2.5知,
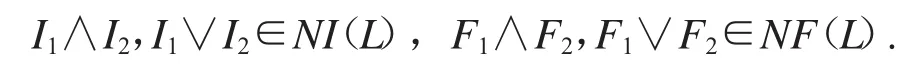
又由定理2.5知,
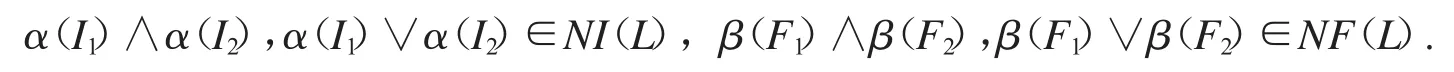
下证 α(I1∧I2)=α(I1)∧α(I2),α(I1∨I2)=α(I1)∨α(I2).
设 x∈α(I1∧I2),则存在 i∈I1∧I2,使得 x≥io.由于 i∈I1,i∈I2,因此 x∈α(I1)且x∈α(I2),故 x∈α(I1)∧α(I2),所以 α(I1∧I2)⊆α(I1)∧α(I2).
另一方面,设 x∈α(I1)∧α(I2),则有 x∈α(I1)且 x∈α(I2).于是存在 i1∈I1,i2∈I2,使得于是又因 i1∧i2≤i1∈I1,i1∧i2≤i2∈I2,故 i1∧i2∈I1∧I2,所以 x∈α(I1∧I2),因此 α(I1)∧α(I2)⊆α(I1∧I2).所以 α(I1∧I2)=α(I1)∧α(I2).
设 x∈α(I1∨I2),则存在 i∈I1∨I2,从而存在 a∈I1,b∈I2,有 i≤a∨b,使得 x≥io.由于 ao∈α(I1),bo∈α(I2),故 x∈α(I1)∨α(I2),即 α(I1∨I2)⊆α(I1)∨α(I2).
另一方面,设 x∈α(I1)∨α(I2),则存在 i1∈α(I1),i2∈α(I2),有 x≥i1∧i2.由 α(I1),α(I2)的定义知,分别存在 j1∈I1,j2∈I2,使得从而又因 j1∨j2∈I1∨I2,于是 x∈α(I1∨I2),所以 α(I1)∨α(I2)⊆α(I1∨I2).因此 α(I1)∨α(I2)=α(I1∨I2).
同理可得 F1∧F2,F1∨F2∈NF(L),有
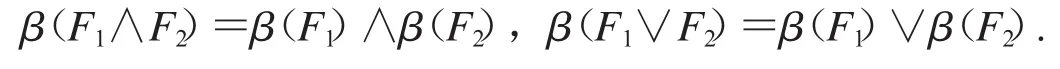
由定理2.4知,β(α(I))=I,α(β(F))=F,所以NI(L)≅NF(L).
3 结束语
本文在文献[5]的基础上,利用双重MS-代数运算及同余性质,论证了获得双重MS-代数正则理想集和正则滤子集是同构的结论.这一结论帮助我们了解双重MS-代数的代数结构.

