基于模糊控制的履带车辆分布式制动系统性能仿真*

朱 昊，张豫南，张舒阳，杨怀彬，房 远

（陆军装甲兵学院，北京 100072）

0 引言

高速履带制动需要的制动功率高，履带车辆上配备单一的机械制动器已经难以满足制动需求，传统的机械摩擦式制动系统有着结构简单、松离彻底性好、造价低廉的优点，但长时间连续制动会导致严重的“热衰退”，制动带容易烧毁，稳定性较差，易刹偏、抱死。该分布式摩擦制动器通过直接作用于履带的方式产生制动效能，作为辅助制动以减小主制动器的压力，分流制动负荷，延长主制动器使用寿命。

通过动力学仿真平台RecurDyn并根据某型履带车辆数据对履带车辆和分布式制动器进行建模，通过对比实验数据建立较为完善的履带车辆模型，并和MATLAB/Simulink仿真平台进行联合仿真，模拟整个制动过程，通过模糊控制来分配制动力应对不同工况需求，优化了制动策略，评估了该方案的可行性［1-16］。

1 制动需求分析

1.1 受力分析

履带模型制动过程受力分析如图1所示。

图1 履带模型制动过程受力分析图

履带车辆水平制动动力学方程：

其中，FB为制动力（联合制动合力）；Ff为滚动阻力；Fw为空气阻力（可忽略）；δ为质量增加系数；G为重力；g为重力加速度；v为车辆速度。

履带车辆的地面变形阻力主要为土壤压实阻力和推土阻力，根据半经验公式将二者结合为一个等效阻力，公式为

可求得滚动阻力Ff。其中滚动阻力系数在车速20 km/h～60 km/h范围内变化小，几乎无影响，不考虑内阻力的影响，根据以往实验将滚动阻力系数设置为0.04。

制动过程中还需克服其质量产生的惯性力，为便于计算，将旋转质量的惯性力矩转化为平移质量力矩，质量增加系数δ作为计入旋转质量惯性力矩后的车辆旋转质量换算系数，其经验公式为

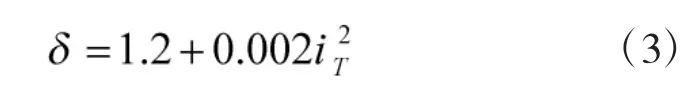
其中，iT为车辆某档位传动系统总传动比，在此取质量增加系数δ为1.2。

1.2 匹配计算

参考国内外相同类型车辆，设定最大减速度为5 m/s2，根据式（1）、式（2），在不考虑空气阻力的情况下，可求得所需制动力

根据方程

可以计算出完全使用摩擦分布式制动器单个制动器所需压力，根据制动力计算结果，本文模型采用4个分布式制动器，取制动器数量n=4；f为履带与制动器间摩擦系数，根据某型履带车辆数据所选择的履带板材料和制动器材料，取摩擦系数f=0.7；FN为每个制动器所需压力。通过计算可得

2 制动系统分析与建模

2.1 履带车辆动力学建模

2.1.1 模型建立

通过多体运动学仿真软件Recurdyn，建立履带车辆模型如图2所示。

图2 履带车辆三维模型

履带模型包括车体、行进机构和分布式制动器3部分。其中行进机构主要由两侧履带子系统构成，分别包括1个主动轮、1个诱导轮、5个托带轮、6个负重轮、103块履带板组成的履带以及悬挂系统。主动轮、诱导轮和托带轮采用转动副和车体连接，悬挂装置主要包括扭杆和平衡轴，通过扭力弹簧与车体连接，负重轮通过转动副与悬挂链接，履带板采用双销式履带，主动轮后置。履带子系统模型如图3所示。

图3 履带子系统模型

2.1.2 模型验证

在动力学模型中，重力加速度g取9.8 m/s2，整车质量为52 000 kg，设置初速度为32 km/h，制动力矩FB=0。根据某型履带车辆实验数据，在滚动阻力与风阻作用下停车的车辆第1次位移为123.41 m，第2次位移118.17 m，第3次位移121.47 m，第4次位移124.26 m，根据仿真结果车辆位移大约为113.74 m，二者结果基本一致，平均误差约为8.08%，说明了模型中的参数基本正确，接近实际情况，曲线如图4所示。

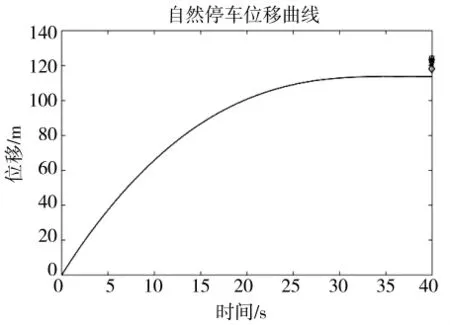
图4 履带车辆自然停车位移曲线

2.2 分布式制动系统建模

2.2.1 模型建立

该分布式制动系统，其制动构件使用RecurDyn进行动力学建模，其机械结构和工作原理如图5所示。

图5 分布式制动器机械结构及原理示意图

分布式制动器位于履带顶面上方部分，分别与两个托带轮相对，球状机构应与履带板凹位充分接触，每条履带上对应两个制动器，这种履带车辆摩擦式制动器包括可任意时间提供制动力且可控制制动力大小的执行机构，以及直接作用于履带产生制动动作的制动构件，执行机构固定于车体上通过液压控制，制动构件在执行机构的带动下朝向履带顶面部分向下运动，与相应的托带轮一起紧抵履带实现制动，或者背离履带顶面部分向上运动而取消制动。其分布示意图如图6所示。

图6 制动器分布示意图

表1 液压数学模型参数表

2.2.2 执行机构建模

执行机构使用液压缸，采用三通电液比例减压阀控制，考虑到漏油、油液的压缩性、负载惯性和阻尼等方面因素的影响，阀控液压缸的负载动态方程如下：

式中参数及物理意义如表1所示。

根据式（5）～式（7）可得比例阀阀芯位移到液压缸输出力的传递函数为：

比例阀存在延时、饱和、滞环以及空行程等非线性环节，相关参数主要为比例阀阀芯位移增益KQ（L·min-1/m）、减压阀阻尼比ζ和减压阀频率ω（Hz）。

履带车辆进行辅助制动时，主要由液压油缸对分布式制动器施加外力，使得制动器朝向履带运动，接触并施压达到制动效果。在不考虑活塞杆空行程情况下，通过MATLAB/Simulink建立的液压控制模型如图7所示，主要参数取值如下页表2所示。

图7 液压控制模型

2.3 机械制动系统建模

某型履带车辆制动器采用弹簧加压干片制动器。为了建立机械制动器模型，在车辆行驶最高速下进行最大制动力试验，即制动踏板踩到底，可以得到车速-时间、制动扭矩-时间曲线如图8所示。

表2 液压控制系统主要参数取值

图8 机械制动器试验曲线

根据上图可以看出机械制动器响应时间约为0.3 s，在高速时制动扭矩较小，在1.2 s时制动扭矩为2 kNm，此后增速放缓，在5.1 s时达到峰值扭矩5 kNm。机械制动系统模型建立在Matlab内，利用该组实验数据来拟合，使之更接近实际制动情况。

2.4 制动踏板建模

制动踏板开合角度为θ，随着制动踏板角度增加，相应制动强度随之增加，在踏板全部踩下即开合度最大时，驾驶员意图为紧急制动，达到最大制动强度。采用模糊控制器建立模型，选取制动踏板开度θ（°）为模糊控制器输入变量，基本论域为［0，60］，取 L（低）、ML（中低）、M（中）、MH（中高）、H（高）5个水平，制动强度z（m/s2）作为模糊控制器的输出变量，基本论域为［0，5］，取 PMIN（正最小）、PS（正小）、PM（正中）、PB（正大）、PMAX（正最大）5个水平，隶属函数均采用三角形，模糊规则曲线如图9所示。

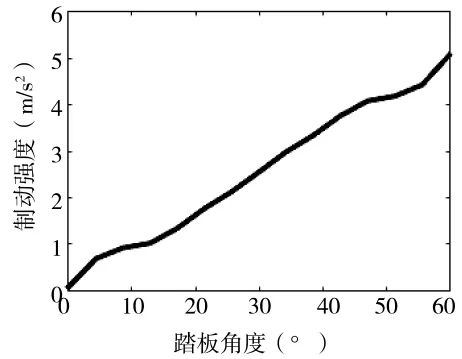
图9 制动踏板模糊规则曲线显示

3 联合制动系统控制策略

3.1 制动策略

联合制动系统由主制动器即车辆原有机械式制动器和辅助式制动器即分布式制动器组成，要达到安全制动、平稳制动以及保护主制动器的目的，履带车辆在行驶过程中，面对不同的行驶条件，控制系统必须能够根据车速和所需制动减速度即驾驶员制动意图的变化来分配制动力。模糊控制具有不依赖于被控对象的精确数学模型、易于被操作人员接受、便于计算机实现和鲁棒性适应性好等优点，本文采用模糊控制策略对主辅制动器的制动力进行分配。

在高速高制动强度制动时摩擦面磨损严重，升温快并且摩擦系数不稳定，使得制动效果不明显，故在高速高强度制动时以分布式摩擦制动器为主，使其承担更多制动能量，而原有机械式制动器低速时制动效能稳定，完全停车效果好，所以在低速低强度时主要以原有机械式制动器为主，提高制动稳定性。

根据联合制动系统特点，制动策略分如下几种情况：

1）车速较高时，利用辅助制动器高速制动效果好的特点，主要使用辅助制动器制动，保护主制动器防止过热及摩擦损坏；

2）车速较低时，由于辅助制动器低速制动效果变弱，因此，此时主制动器开始工作，现处于主辅制动器同时工作状态；

3）紧急制动时，协调主辅制动器使其分别在最佳状态制动使得整体达到紧急制动效果。

3.2 模糊控制器设计

3.2.1 模糊语言变量

根据系统控制策略需求，选取制动强度z（m/s2）和履带车辆速度v（m/s）作为模糊控制器的输入变量，主制动力分配系数σ1和辅助制动力分配系数σ2为输出变量。

其中输入变量制动强度z（m/s2）的基本论域为［0，5］，履带车辆速度 v（m/s）的基本论域为［0，25］，两个输入变量均取 L（低）、ML（中低）、M（中）、MH（中高）、H（高）5个水平。输出变量主制动力分配系数σ1和辅助制动力分配系数σ2的基本论域为［0，1］，取 ZO（零）、PMIN（正最小）、PS（正小）、PM（正中）、PB（正大）、PMAX（正最大）。

3.2.2 变量隶属函数

模糊控制器输入变量和输出变量均采用三角形隶属函数，具体变量隶属函数如图10所示。

图10 变量隶属函数

3.2.3 模糊控制规则

根据联合制动策略，建立相应的模糊控制规则，具体如表3所示。

表3 模糊控制规则

输出变量的曲面观测窗如图11所示，可以看出输出变量滓1和滓2是两个输入变量z和v的函数。

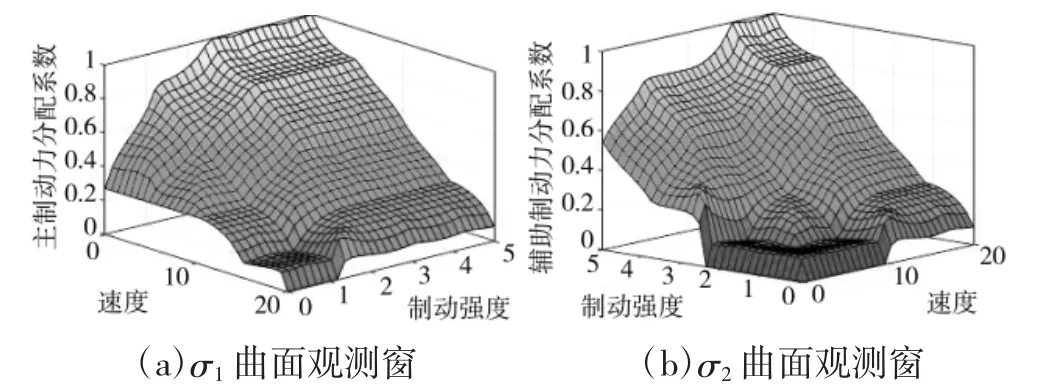
图11 输出变量曲面观测窗

4 仿真与分析

4.1 独立制动仿真

4.1.1 主制动器紧急制动

对动力学模型仅在机械制动系统下制动进行仿真，初速度20 m/s，在1 s后施加制动，其速度等参数变化曲线如图12所示。

图12 主制动器制动速度等变化曲线

4.1.2 辅助制动器紧急制动

设置履带车辆初始速度为22 m/s，在行驶0.5 s后施加制动，完全使用摩擦分布式制动器，即每个制动器上施加大小为FN的垂直压力，其速度变化曲线如下页图13所示。

可以看出制动效果响应较快，在高速状态下制动效果明显，制动减速度很大，随着速度的减小，制动减速度也相应减小，平均制动减速度接近预期值。

4.2 联合制动仿真

4.2.1 联合制动模型构成

由原有机械制动系统和新型分布制动系统构成的履带车辆联合制动模型主要由制动踏板信号模块、制动力分配模块、机械制动模块、分布式制动模块和动力学模型模块等组成。其中制动踏板信号作为一个输入来模拟驾驶员在车辆制动过程中的踏板力度；机械制动模块和分布式制动模块根据制动力分配情况进行制动，其中机械制动为主，分布式制动为辅；动力学模型模块进行复杂的运动计算，可以实时反馈车辆速度变化情况；制动力分配模块作为是联合制动系统的中心，它根据制动踏板信号、动力学模型中的速度反馈信号分配制动力，进而达到预期制动效果。在MATLAB/Simulink中建立履带车辆分布式制动模糊控制系统仿真模型如图14所示。

4.2.2 联合仿真

对输入制动踏板角度为60°即紧急制动强度、输入40°即中等制动强度和输入20°即一般制动强度3种情况进行仿真，初速度为20 m/s，在一秒钟时施加制动，结果如图15～图17所示。

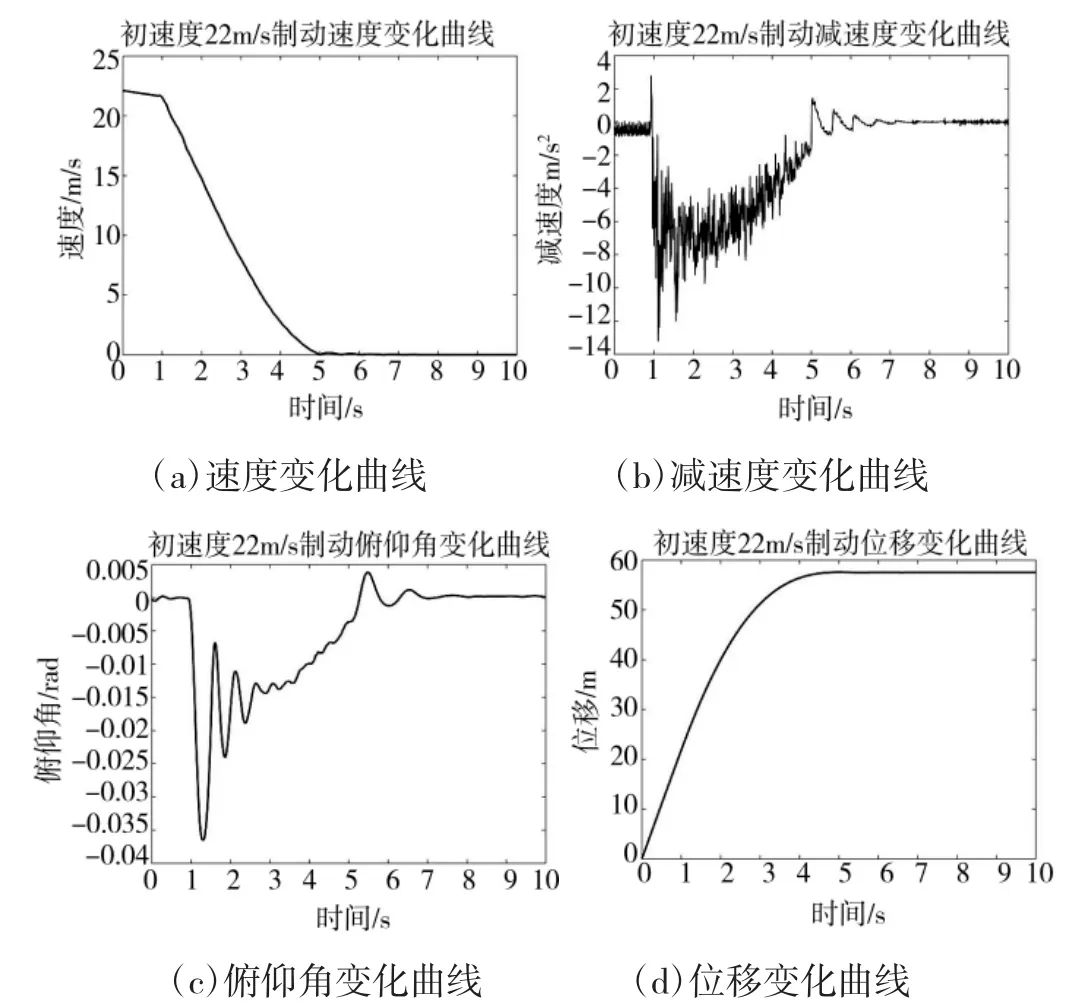
图13 辅助制动器制动速度等变化曲线

图14 履带车辆分布式制动模糊控制系统仿真模型

图15 紧急制动强度

图16 中等制动强度

从曲线可以看出，随着制动强度增加，辅助制动器参与制动比例随之增加，在紧急制动强度下，承担了近2/3的制动能量，随着制动强度降低，主制动器参与制动比例增加，在一般制动强度中，辅助制动器也承担了近1/3的制动能量，说明了辅助制动器能够有效地分担主制动器压力、分流制动负荷。在制动过程中，车速越高，辅助制动器参与制动比例越大，而随着车速降低，主制动器介入制动比例增加，并且在高速运动情况下，分布式制动器能够提供足够大的制动强度，承担了绝大部分制动能量，从而解放主制动器，相应地减少其磨损和发热等影响，延长其使用寿命。

图17 一般制动强度

还可以看出分布式制动器制动介入时速度曲线出现一定波动，相对而言主制动器波动较小，主要原因为分布式制动器在与履带板作用时，由于履带板自由度较高，波动性较大，与分布式制动器频繁撞击而产生的效果，就车辆整体而言，无论是俯仰角度还是车速变化急缓趋势，均处于相对稳定的范围内，模糊控制器发挥了其作用，面对不同工况分配制动力，制动相对平稳。

5 结论

提出了一种新型的履带车辆分布式制动系统，利用现有动力学仿真平台，对履带车辆分布式制动模型进行搭建及仿真，并对履带车辆原有机械制动系统和分布式制动系统组成的联合制动系统进行了分析，建立了联合仿真模型，评估了该方案，证明了该方案技术可行。

提出了基于模糊控制的制动力分配策略，能够实现在不同工况下主辅制动力的合理分配，并且系统较小超调，在整个制动过程中辅助制动承担了大部分能量，从而主制动器使用频率减少，使用寿命可以延长，依靠履带耐磨性较强的特点，直接在履带上施加制动不会对履带造成额外损伤，同时制动器和履带都在车体外部，便于拆卸修理，分布式又可以进行独立控制，可控性适应性更强。

由于履带车辆行驶工况比较复杂，所考虑到的因素较少，与实际还有差别，模糊控制器的设计还有很多值得改进的地方，分布式制动器的机械结构也有待完善，在下一步的工作中会对控制策略和机构的合理性、有效性进行进一步的论证和完善。