采用二维CZT的MIMO雷达极坐标格式成像算法*
赵小茹,童宁宁,胡晓伟,丁姗姗
(空军工程大学防空反导学院,西安 710051)
0 引言
目前,实现MIMO雷达成像[1-2]的算法主要分为时域和波数域两类。时域中,利用后向投影(BP)算法可以实现小型MIMO雷达成像[3],降低阵列规模和硬件复杂度;波数域中,分析目标波数谱的支撑区范围,根据逆散射理论可以成像,文献[4]讨论MIMO雷达收/发阵列排布的空间谱域,提出空间谱域填充实现成像。
极坐标格式(Polar Format Algorithm,PFA)[1]算法,最早应用于聚束SAR,以极坐标格式录取数据,通过内插运算实现坐标轴转换,内插精度对成像质量和运算效率起关键作用。近年来,该算法被逐步引入ISAR成像系统中[5-6],有学者将其与MIMO雷达相结合[7]。文献[8]提出一种快速极坐标转换的成像算法,利用变换因子避免二维内插运算,降低运算复杂度,仿真主要针对理想环境,忽略复杂情况、噪声等带来的影响,故MIMO雷达极坐标成像算法有待研究。
本文将Chirp-Z变换(CZT)应用于MIMO雷达PFA算法,对雷达回波信号的波数谱在距离向和方位向进行二维CZT变换,完成波数谱由不均匀的扇形分布向均匀矩形分布的转换,达到与二维插值处理相同的坐标转换效果。
1 MIMO雷达成像回波信号模型
建立MIMO雷达成像空间分布模型,雷达收发阵列共线排布(沿直线y=ya),取平行于阵列的直线为x轴。指定散射点模型中一点为参考中心并定为原点O(xo,yo)。发射阵元和接收阵元分别以3d和d的间距均匀排布,如图1所示。

图1 MIMO雷达成像空间分布
根据相位中心近似原理(Phase Center Approximation,PCA)[9-10]得到间距均为d/2的等效阵元(xe,ya),中心阵元的缺失对整个阵列影响较小[5]。任一散射点(xp,yp)与第 m 个发射阵元(xtm)和第 n 个接收阵元(xrn)的距离为

考虑阵列与目标的距离远大于阵元的间距,通过 Fresnel近似[8],距离和为

假设各发射阵元发射载频相同、带宽相等的宽带信号
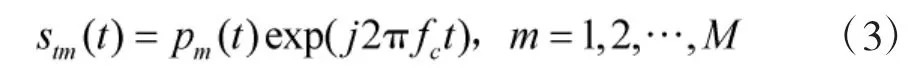
其中,fc为载频;pm(t)为调制复包络,满足,为发射信号持续时间,f(t)为匹配滤波器输出,理想情况下pm(t)近似为冲激函数并用 p(t)表示。
经相干检波得到基频回波信号为

其中,σi为第i个散射点回波的幅度。
对式(4)在频域进行匹配滤波得

其中,fb为匹配滤波时的采样频率。
以参考中心为基准,对式(5)相位补偿得

其中

定义系数变换如下
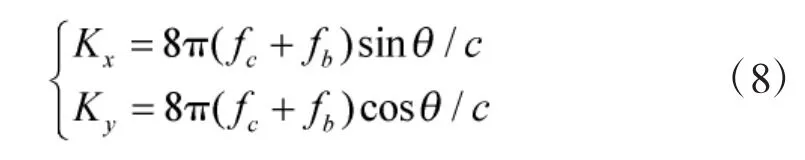
将式(8)带入式(6)得到回波信号波数域的表达式

夹角和频率的变化使得MIMO雷达等效阵列回波信号在波数域中的采样点呈扇形,如下页图2所示。

因为不具备矩形网格点的数据结构,若对图2所示扇形波数谱直接进行二维IFFT处理,无法得到准确的成像结果,所以需要通过插值处理转换波数谱,得到图2红点部分表示的矩形数据结构。经典PFA算法即利用二维插值处理实现波数谱向矩形分布的转换,校正目标的距离徙动,消除信号波数域距离向和方位向的耦合[11-12],而后进行FFT运算可以实现成像,但存在运算量大、复杂度高的问题。
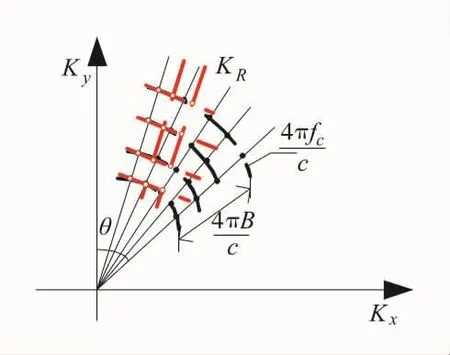
图2 波数谱分布图
2 MIMO雷达成像极坐标格式算法
2.1 CZT变换的基本原理
CZT变换[13-17]实现Z平面上沿部分单位圆的均匀采样,定义为
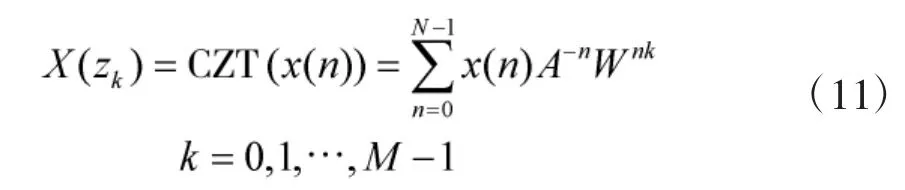
其中,系数 A,W 如式(11)所示
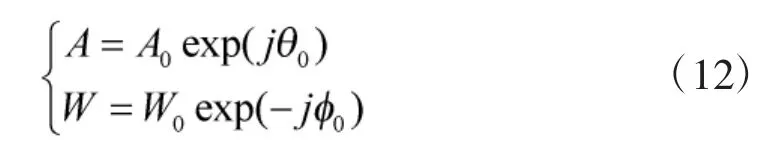
2.2 基于CZT变换的极坐标格式算法
采用CZT变换确定参数,完成二维尺度变换实现坐标系的转换。将式(9)离散化表示为

其中,Nx为等效阵元数目,Nf为匹配滤波器频率采样点数;,fbj为采样频率,θi为第 i个等效阵元的指向,对应与坐标xe。类比得到式(8)的离散化表示为

距离向尺度变换的目的是为消除波数向量夹角θi的变化对的影响,因此,需选定一个基准阵元,即确定其的指向为基准角度,使得对任一fbj值,都满足。本文以θi=0 rad对应的阵元为基准阵元,带入式(14)得

展开式(15)得



式(18)说明,距离向尺度变换后,消除了波数域中信号的距离信息y与夹角θ的耦合,即距离信息y与方位向的耦合,将扇形波数谱转换为楔形,可以直接进行距离向IFFT。
对比式(13)和式(18)得到

利用CZT变换实现距离向的尺度变换,需要选择合适的幅角θ0和幅角增量φ0确定参数,得到与插值处理效果一致的波数域分布。基于式(10)得出CZT变换参数为

距离向的尺度变换将引起方位向波数域坐标改变,即

对方位向进行尺度变换的目的是为消除匹配滤波采样频率fbj的变化对的影响,与距离向尺度变换过程相似,以选取基准阵元,带入式(14)得到,

展开式(22),得


二维CZT变换后的信号波数域表示式为
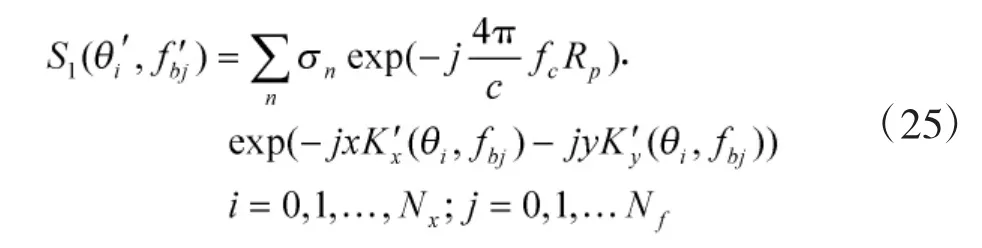
其中


图3 基于CZT的PFA算法流程图
3 仿真实验
仿真采用一组4个40码元的四相编码正交信号为发射信号,载频10 GHz,子脉冲宽度2 ns,对应信号带宽500 MHz。收发阵列排布类比图1,发射阵元、接收阵元各10个,间距d=10 m。目标由11个散射点组成,以目标中心建立二维直角坐标系,空间二维分布如图4所示。
分别用3种处理方法实现PFA算法,得到成像结果如图5所示。

图4 散射点模型

图5 PFA算法的成像结果
图5(a)为直接采用FFT成像的结果,可以看出随着散射点横向距离的增大,边缘点存在散焦现象,而且方位向的估值存在较大误差。图5(b)为利用二维插值处理的成像结果,与图5(a)相比,聚焦性能提升,但边缘点聚焦性能欠佳。图5(c)采用CZT变换成像,由于旁瓣略高存在散焦现象,但二维成像的性能和坐标值估计的精确度与二维插值处理基本一致,且边缘点的聚焦性能优于前两种方法。给定信噪比为-15 dB,3种处理方法的成像结果如图6所示。

图6 加入噪声的成像效果
图6(a)为直接进行FFT运算成像的结果,存在散焦现象且方位向估值精度差。图6(b)为利用二维插值处理方法成像的结果,可以较为精确地实现成像,但散射点方位向坐标的增大使其出现散焦。图6(c)为基于二维CZT变换成像的结果,虽然聚焦性能劣于图6(b),但其边缘点的成像质量良好且运算速度快。
设定单散射点(-0.6,1.6),分别仿真其在距离向和方位向的一维像如图7所示。图7(a)为距离向一维剖面图,图7(b)为方位向一维剖面图。
图7(a)说明3种处理方法在距离维估值准确且峰值明显。图7(b)说明进行方位维估值时,直接FFT运算存在误差较大,插值处理得到的估值最准确,而基于二维CZT变换的处理方法存在误差,但近似等于准确值,误差可接受。
给定信噪比SNR=-15 dB,单个散射点(-0.6,1.6)的方位向一维剖面图如图8所示。

图7 点目标距离向和方位向剖面图

图8 单点方位向剖面图(1 000次蒙特卡洛试验)
可以看出,基于二维CZT变换得到峰值更为明显,优于二维插值处理,旁瓣更低,易于判断,保证更好的成像性能。
控制采样次数分别为 H=128,256,512,1 024次,对比采用CZT变换和二维插值处理两种处理方法的运算时间,如图9所示。

图9 运算时间对比图
可以看出,随着采样次数的增加运算时间也在延长,基于CZT变换的PFA算法的运算时间明显少于二维插值处理,体现了所提算法对运算时间的节省。
4 结论
本文基于MIMO雷达回波信号空间波数域分布和波数谱支撑区范围,针对经典PFA算法中插值运算存在复杂度高和运算量大的问题,提出基于二维CZT变换的PFA算法。仿真试验表明,不同仿真条件下,本文所提算法能够在保证成像质量的同时降低运算复杂度并有效地减小运算时间,验证了该算法的可行性。

