基于网格聚类的弹道目标航迹起始算法*

赵崇丞，王 君，邵 雷

（空军工程大学防空反导学院，西安 710051）

0 引言

航迹起始是多目标跟踪中的首要问题，起始速度的快慢及准确性对航迹处理的后续过程，航迹关联及跟踪滤波的性能有着很大的影响。

目前，航迹起始算法主要包括顺序处理算法和批处理算法。其中，在相对无杂波的环境中起始目标航迹一般采用顺序处理算法，如直观法、逻辑法、修正逻辑法，这类算法在相对弱杂波环境下能较好地起始目标航迹，适合工程运用，但是在强杂波环境下，容易起始虚假航迹。而批处理算法，如Hough变换法等，在强杂波的环境下起始目标航迹具有很好的效果，但当杂波过于密集时，起始计算量太大，难于工程实现。

文献［1］利用位置信息形成可能航迹，在采用椭圆形波门的同时，附加一定角度限制，并利用红外被动跟踪的灰度信息去除掉了部分杂波，但其产生了较多的虚假航迹。文献［2］首先为每个量测点分配一定的特征值，然后通过基于蚁群的拾起和放下的方法计算所需起始目标航迹数，最后采用模糊蚂蚁聚类算法生成目标航迹。在弱杂波环境中，该算法起始目标航迹的实时性及准确性都较高，然而在高密度杂波环境下，航迹起始实时性有待提高。文献［3］提出一种假目标干扰条件下起始断续点迹的算法，该算法通过序列检测技术制定采样终止规则以过滤虚假关联，构建飞行特征限制映射参数集来剔除虚假航迹，解决了航迹簇拥下的检测和估计问题，但由于该算法较为繁琐，导致达不到实时性的要求。

弹道目标在再入段飞行时，飞行速度快，飞行时间短，而且真弹头的周围有多个重诱饵，加之所处的杂波环境使得起始多个弹道目标变得十分困难，对航迹起始的准确性和实时性产生了很大的影响。为了提高弹道目标航迹起始的准确性和实时性，本文提出了一种基于网格聚类的弹道目标航迹起始方法。首先将雷达探测到的所有点迹映射到网格中，并利用网格聚类中的密度阈值区分出高低密度网格；其次为了提高聚类精度，采用边界点提取技术提取低密度网格中的有效点迹，接着去除掉低密度网格中的剩余点迹，然后利用网格核技术将高密度网格处理成簇，以提高航迹起始的准确性。最后对每个簇进行聚类处理［4-6］，并对每个聚类使用修正逻辑法进行航迹起始，以避免其他高密度网格中的点迹干扰。实验仿真表明，该方法能以较高的精度起始弹道目标航迹，且实时性好。

1 网格聚类算法

1.1 网格的基本概念

1.2 相似度

雷达探测到的点迹之间的距离决定它们的相似性。两数据点之间的距离越小，它们归属同一类的概率就越大，相似度也越大［7］。

定义1设S中点迹对象Zi的属性值Pi由n维向量表示，定义Zi与S中任意一个点迹Zj间的相异度diff（i，j）和相似度sim（i，j）的定义如下：

1.3 边界点提取技术

在判定完所有高低密度网格后，低密度网格中个别点迹Ri可能源于真实目标，Ri也即边界点。采用传统的网格聚类算法时，往往把低密度网格中的全部点迹当作杂波丢弃掉，但当真实目标点迹落入低密度网格时，丢弃所有点迹会影响起始精度，甚至导致航迹丢失。因此，为了提高聚类精度，引入边界点函数borderf（i）和边界点阈值函数minf（i），它们的定义分别如下：

其中，nk表示某高密度网格中回波点迹数，k表示该高密度网格中第k个点迹，sim（i，k）为高密度网格中第k个点迹与低密度网格中第i个点迹间的相似度。

边界点提取技术的核心思想：遍历所有高密度网格，若某个高密度网格周围存在一个或多个低密度网格，则针对这些低密度网格中的点迹Ri进行判别，如果边界点函数borderf（i）大于等于边界点阈值函数minf（i），则Ri为该高密度网格中的边界点，即Ri属于该高密度网格。如果多个高密度网格共同占有一个低密度网格，则需要采用广度优先原则对边界点进行提取。提取完所有高密度网格的边界点后，可认为低密度网格中的所有点迹均为杂波点，并将这些杂波点丢弃掉。完成对边界点的提取后，不仅从低密度网格中提取出了有效点迹，而且丢弃了部分虚假点迹，提高了聚类精度，进而航迹起始准确度得以提高。

1.4 网格核技术

经过边界点提取技术处理过后，某个目标4个时刻的雷达探测点迹可能处于两个或以上的高密度网格中，故不能直接对高密度网格中的点迹进行聚类。因此，利用网格核技术来提高航迹起始准确度。

网格核由高密度网格中所有相似点迹构成，它表示一个簇，能吸引其周围高密度网格中的相似数据点迹形成同一个类。

网格核技术的核心思想：经过边界点提取处理后，遍历与每个高密度网格Cn相邻的高密度网格中的点迹v，若v至少与Cn中个点迹相似（如果两个点迹间的相似度不小于给定阈值minsim），则点迹v与高密度网格Cn属同一簇C。

2 修正逻辑法

逻辑法对雷达连续扫描期间接收到的顺序观测值进行处理，观测值序列表示n次雷达扫描的时间窗的输入，当时间窗里的检测数达到指定门限m时便可成功起始一条航迹，否则就把时间窗向增加时间的方向移动一次，此即逻辑法采用的m/n滑窗法［8］。其原理如图1所示。

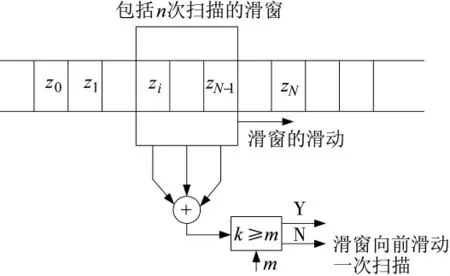
图1 基于m/n逻辑原理的滑窗法

式中，t为雷达扫描周期。假设观测误差是独立、零均值、并服从高斯分布的，其协方差为Ri（k），则归一化距离平方为

式中，Dij（k）为服从自由度为p的分布的随机变量。根据给定的门限概率和自由度p查分布表可得门限γ，若Dij（k）≤γ，则可判定量测Zi（k）与Zj（k+1）互联。

在虚警概率高的情况下，逻辑法起始速度慢且容易产生较多虚假航迹［12］。为了提高起始目标航迹的速度，可在逻辑法的基础上，对落入相关波门中的量测点增加角度限制条件，以剔除与航迹在一定程度上成V字形的测量点迹［13］。

3 基于网格聚类的弹道目标航迹起始算法

针对弹道目标航迹起始，在密集杂波的环境下，雷达每个时刻探测到的点迹除了多个弹道目标点还有许多杂波点。则每一时刻进入相关波门的点迹中除了真实点迹，还会包含部分杂波或噪声点迹［11-15］。为了快速起始航迹，并提高航迹起始准确度，首先引入网格聚类来去除部分杂波，再对雷达探测到的4个时刻的点迹进行聚类，最后对每个类采用修正逻辑法进行航迹起始。具体步骤如下：

1）将三维空间的每一维M等分，形成M3个网格单元。

2）对雷达4个时刻探测到的点迹集R进行遍历，并将R中点迹对象映射到网格。

3）根据密度阈值minPts判定出每个网格是高密度网格还是低密度网格。

4）考察每个高密度网格相邻的低密度网的点迹Ri，若该点迹的边界点函数值borderf（i）大于等于边界点阈值minf（i），则点迹Ri是该高密度网格的边界点。

5）边界点提取完成后，对所有高密度网格采用广度优先原则进行网格核技术处理，形成簇［9］。

6）经过网格核技术处理后，对每个簇中任意两点Ri和 Rj，如果它们的相似度满足：sim（i，j）≥minsim，则把点迹Ri和Rj归一类。

7）完成聚类后，对每个类中点迹按接收时间排序，然后对其采用修正逻辑法。整个算法流程图如下页图2所示。

4 仿真及结果分析

4.1 仿真设置

为了验证本文方法起始弹道目标航迹的效果，及分析引入网格聚类后对航迹起始的影响。在高密度杂波环境下进行仿真实验，并与逻辑法，3/4修正逻辑法进行了比较。

使用某型三坐标相控阵雷达对4个弹道目标进行跟踪，以雷达站（91.1 E，29.4 N）为原点建立北天东坐标系。4个弹道目标的初始位置为（-51 743 m，44245m，79865m），（-39273m，66929m，80465m），（-73253m，28669m，80940m），（-7046m，79356m，70 986 m）。雷达的采样周期为T=6 s，雷达的测距精度为150 m，测角精度为0.5（包括高低角和方位角）。每个周期的杂波个数由泊松分布确定，即给定参数，首先产生（0，1）区间上均匀分布产生的随机数 r，然后按式（7）所示：

确定出J后，每个周期在雷达视野范围内随机产生J个杂波，且这J个杂波服从均匀分布。取M=6，密度阈值minPts=2。

图2 基于网格聚类和修正逻辑法的航迹起始流程图

4.2 仿真分析

由图5～图7可以看出，基于网格聚类的弹道目标航迹起始效果最佳，基于修正逻辑的航迹起始次之，最差的是基于逻辑法的航迹起始。其中，基于逻辑法和修正逻辑法的航迹起始均出现了航迹分叉，受杂波影响较大。

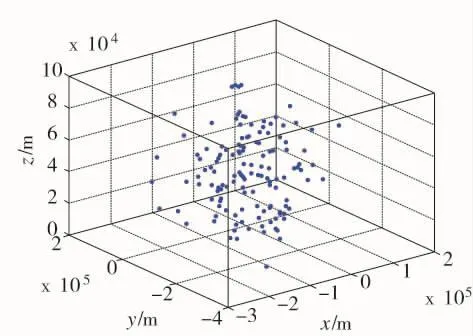
图3 目标和杂波点迹态势图

图4 杂波点和基于网格聚类的弹道目标航迹起始图

图5 基于网格聚类的弹道目标航迹起始图

图6 基于逻辑法的弹道目标航迹起始图

图7 基于修正逻辑法的弹道目标航迹起始图

不同杂波数量下，分别采用逻辑法、修正逻辑法和基于网格聚类的方法进行50次蒙特卡洛仿真实验，各方法的平均运行时间如表1所列。由表1可知，逻辑法和修正逻辑法的运算量在同一个级别，当杂波数较小时，基于网格聚类方法的运行时间要长于以上两种方法的运行时间，但当杂波越来越密集时，基于网格聚类方法的实时性就表现得很好，运行时间明显优于以上两种方法的运行时间。

表1 逻辑法、修正逻辑法、本文方法的平均运行时间（s）统计

5 结论

弹道目标在再入段飞行速度快，真弹头周围伴飞有重诱饵，加上高密度杂波的影响，雷达对弹道目标的航迹起始较为困难，本文采用基于网格聚类的方法对弹道目标进行航迹起始，并与传统航迹起始算法进行比较，仿真结果表明该算法利用网格聚类去除了部分杂波，成功起始了弹道目标航迹，提高了航迹起始准确性，解决了高密度杂波环境下虚假航迹多的问题，同时在密集杂波条件下，该算法航迹起始实时性较好，在弱杂波条件下航迹起始实时性有待提高，适于高密度杂波条件下的工程应用。