中考课题学习型试题

文 /邓革周

课题学习型试题常以几何图形为题材，或以数学问题为背景，通过对相关问题的描述或逐步观察、操作、探究，进而发现问题，解决问题.中考课题学习型试题常见的有三种：操作发现型、猜想论证型、类比探究型.

一、操作发现型

例1【操作发现】如图1，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．

（1）请按要求画图：将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连接BB′；

【问题解决】

如图2，在等边三角形ABC中，AC=7，点P在△ABC内，且∠APC=90°，∠BPC=120°，求△APC的面积．

小明同学通过观察、分析、思考，对上述问题形成了如下想法：

想法一：将△APC绕点A按顺时针方向旋转60°，得到△AP′B，连接PP′，寻找PA，PB，PC三条线段之间的数量关系；

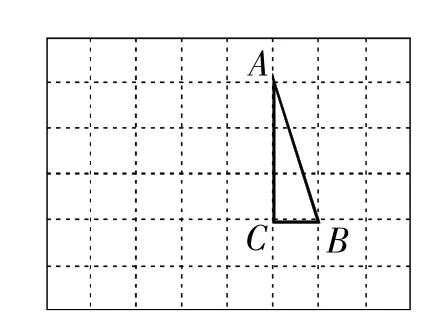
图1

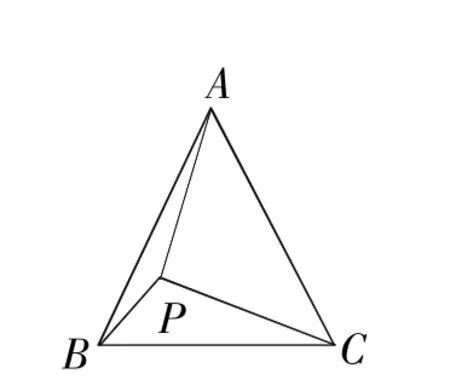
图2

想法二：将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，连接PP′，寻找PA，PB，PC三条线段之间的数量关系.

……

请参考小明同学的想法，完成该问题的解答过程.（一种方法即可）【灵活运用】

如图3，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE=∠ADC，BE=CE=2，CD=5，AD=kAB（k为常数），求BD的长（用含k的式子表示

图3

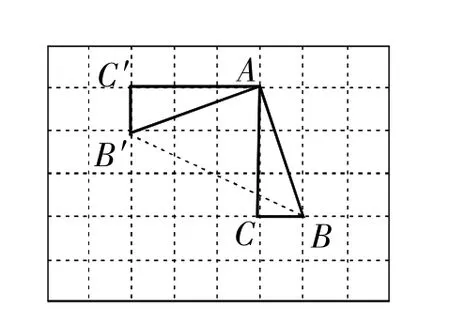
图4

图5

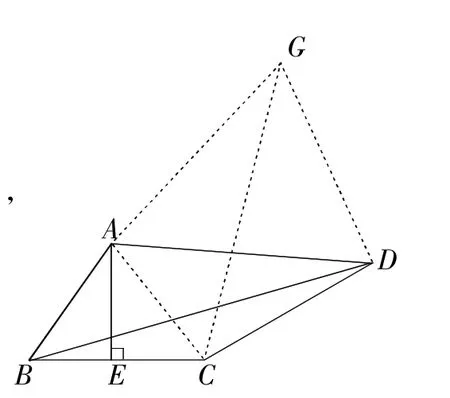
图6

解：【操作发现】（1）如图4所示，△AB′C′即为所求.

（2）连接BB′，

∵AB=AB′，∠B′AB=90°，∴∠AB′B=45°.

【问题解决】如图5，

将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，

∴△APP′是等边三角形，

∠AP′C=∠APB=360°-90°-120°=150°，

∴∠PP′C=∠AP′C-∠AP′P=150°-60°=90°，

∠P′PC=∠APC-∠APP′=30°，

∵∠APC=90°，∴AP2＋PC2=AC2，即

【灵活运用】如图6，∵AE⊥BC，BE=EC，∴ AB=AC，

将△ABD绕点A逆时针旋转得到△ACG，连接DG，则BD=CG，

∵∠BAD=∠CAG，∴∠BAC=∠DAG.

∵AB=AC，AD=AG，∴∠ABC=∠ACB=∠ADG=∠AGD，

∴△ABC∽△ADG.

∵AD=kAB，∴DG=kBC=4k.

∵∠BAE+∠ABC＝90°，∠BAE=∠ADC，∴∠ADG+∠ADC=90°

二、类比探究型

例2问题背景：已知∠EDF的顶点D在△ABC的边AB所在直线上（不与A，B重合），DE交AC所在直线于点M，DF交BC所在直线于点N，记△ADM的面积为S1，△BND的面积为S2．

（1）初步尝试：如图7，当△ABC是等边三角形，AB=6，∠EDF=∠A，且DE∥BC，AD=2时，则

（2）类比探究：在（1）的条件下，先将点D沿AB平移，使AD=4，再将∠EDF绕点D旋转至如图8 所示位置，求S1·S2的值；

（3）延伸拓展：当△ABC是等腰三角形时，设∠B=∠A=∠EDF=α．

（i）如图9，当点D在线段AB上运动时，设AD=a，BD=b，求S1·S2的表达式（结果用a，b和α的三角函数表示）；

（ii）如图10，当点D在BA的延长线上运动时，设AD=a，BD=b，直接写出S1·S2的表达式（不必写出解答过程）．

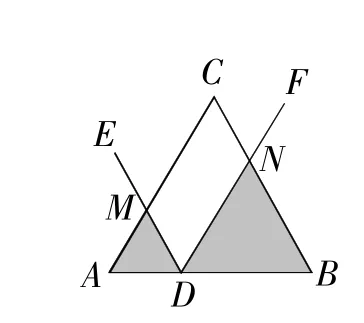
图7

图8

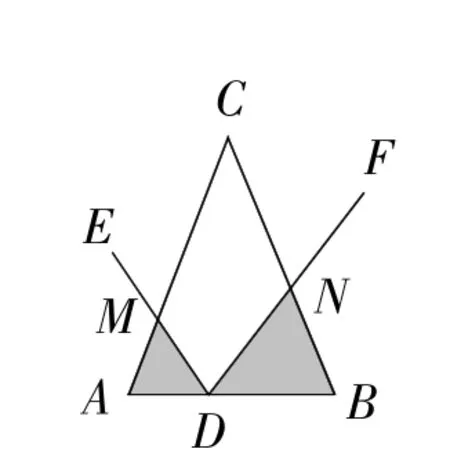
图9

图10

解：（1）如图7，∵△ABC是等边三角形，

∴AB=CB=AC=6，∠A=∠B=60°，

∵DE∥BC，∠EDF=60°，∴∠BND=∠EDF=60°，

∴∠BDN=∠ADM=60°，∴△ADM，△BDN都是等边三角形，

（2）如图8，设AM=x，BN=y.

∵∠MDB=∠MDN+∠NDB=∠A+∠AMD，∠MDN=∠A，

∴∠AMD=∠NDB，

∵S1＝

∴S1·

（3）（i）如图9，设AM=x，BN=y，

同法可证△AMD∽△BDN，可得xy=ab，

（ii）如图10，设AM=x，BN=y，

同法可证△AMD∽△BDN，可得xy=ab，

∵S1=（ab）2sin2α．

三、猜想论证型

例 3 如图11，在Rt△ABC中，∠A=90°，AB=AC，点D，E分别在边AB，AC上，AD=AE，连接DC，点M，P，N分别为DE，DC，BC的中点.

（2）探究证明：把△ADE绕点A逆时针方向旋转到图12的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；

（3）拓展延伸：把△ADE绕点A在平面内自由旋转，若AD=4，AB=10，请直接写出△PMN面积的最大值.

解：（1）∵点M，P，N是DE，CD，BC的中点，

∵AB=AC，AD=AE，∴BD=CE，∴PM=PN.

∵PN∥BD，∴∠DPN=∠ADC.

∵PM∥CE，∴∠DPM=∠DCA.

∵∠BAC=90°，∴∠ADC+∠ACD=90°，

∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°，∴PM⊥PN，

故答案为：PM=PN，PM⊥PN.

（2）由旋转知，∠BAD=∠CAE，

∵AB=AC，AD=AE，∴△ABD≌△ACE，

∴∠ABD=∠ACE，BD=CE，

图11

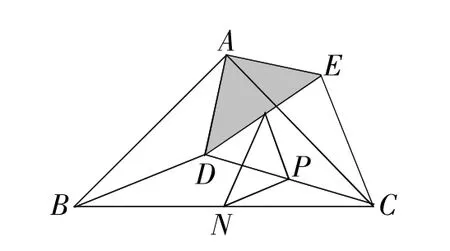
图12

∴PM=PN，∴△PMN是等腰三角形，

同（1）的方法得，∠DPM=∠DCE，∠PNC=∠DBC，

∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC，

∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC

=∠ACB+∠ACE+∠DBC

=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC=90°，

∴△PMN是等腰直角三角形.

图13

∴PM最大时，△PMN面积最大，∴点D在BA的延长线上，

∴BD=AB+AD=14，∴PM=7.

∴S△PMN最大=