生活中的图表信息题

文/谢春娟

图表信息题是指通过图形、图文、图象、表格、统计图表等形式呈现信息，要求考生通过观察、比较、分析、筛选，从中获取有用的信息，进而建立数学模型，从而使所给问题得以解决的一类题型．现把图表信息题归类总结如下.

一、图形信息题

例1如图1，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房大长方形的周长，则分割后不用测量就能知道周长的图形标号为（ ）

A.①②. B.②③.

C.①③. D.①②③.

解析：设原住房大长方形的周长为2l，长方形①的长和宽分别为a，b，正方形②和③的边长分别为c，d.由图1得

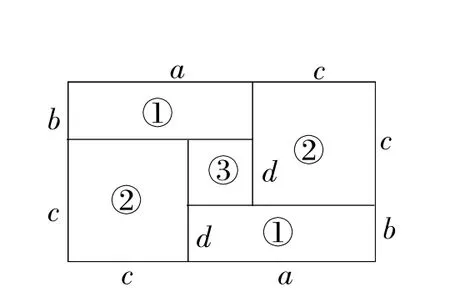
图1

①-②，得a-c=c-b，即a+b=2c.将a+b=2c代入③，得4c=l，即（定值）；将代入a+b=2c，得即2（a+b）=l（定值）；由已列方程组得不到d关于l的代数式.

∴分割后不用测量就能知道周长的图形标号为①②.选A.

二、图文信息题

例2学校“百变魔方”社团准备购买A，B两种魔方，已知购买2个A种魔方和6个B种魔方共需130元，购买3个A种魔方和4个B种魔方所需款数相同．

（1）求这两种魔方的单价；

（2）结合社团成员的需求，社团决定购买A，B两种魔方共100个（其中A种魔方不超过50个）．某商店有两种优惠活动，如图2所示．请根据以上信息，说明选择哪种优惠活动购买魔方更实惠．

解析：（1）设A种魔方的单价为x元/个，B种魔方的单价为y元/个.

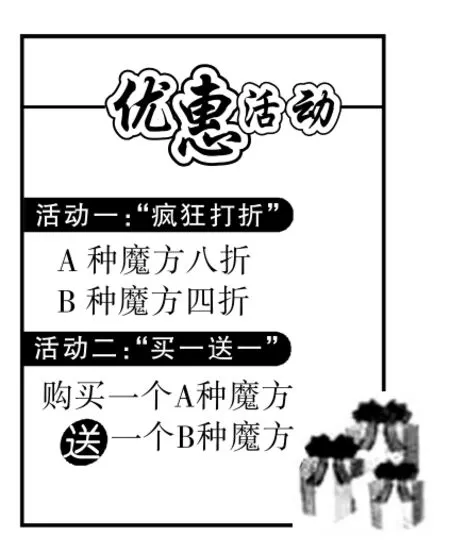
图2

答：A种魔方的单价为20元/个，B种魔方的单价为15元/个．

（2）设购进A种魔方m个（0≤m≤50），总价格为w元，则购进B种魔方（100-m）个.

根据题意得w活动一=20m×0.8+15（100-m）×0.4=10m+600；

w活动二=20m+15（100-m-m）=-10m+1500．

当w活动一＜w活动二时，有10m+600＜-10m+1500，解得m＜45；

当w活动一=w活动二时，有10m+600=-10m+1500，解得m=45；

当w活动一＞w活动二时，有10m+600＞-10m+1500，解得45＜m≤50．

答：当m＜45时，选择活动一购买魔方更实惠；当m=45时，两种活动费用相同，可任选一种活动购买魔方；当45＜m≤50时，选择活动二购买魔方更实惠．

18

三、图象信息题

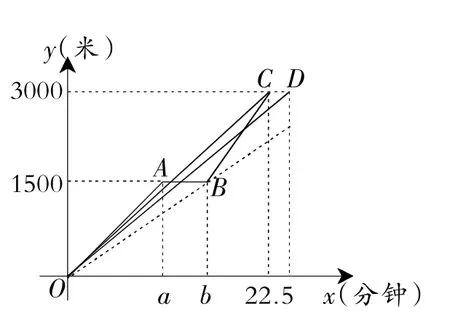
图3

例3“低碳环保、绿色出行”的理念得到广大群众的接受，越来越多的人喜欢选择自行车作为出行工具．小军和爸爸同时从家骑自行车去图书馆，爸爸先以150米/分的速度骑行一段时间，休息了5分钟，再以m米/分的速度到达图书馆．小军始终以同一速度骑行，两人行驶的路程y（米）与时间x（分钟）的关系如图3．请结合图象，解答下列问题：

（2）若小军的速度是120米/分，求小军在途中与爸爸第二次相遇时，距图书馆的距离；（3）在（2）的条件下，爸爸自第二次出发至到达图书馆前，何时与小军相距100米？

（4）若小军的行驶速度是v米/分，且在途中与爸爸恰好相遇两次（不包括家、图书馆两地），请直接写出v的取值范围．

∵爸爸休息了5分钟，∴b=a+5=10+5=15.

∵（3000-1500）÷（22.5-15）=1500÷7.5=200，∴m=200.（2）设BC的函数关系式为y=kx+b，

∴BC的函数关系式为y=200x-1500.

∵小军的速度是120米/分，

∴OD的函数关系式为y=120x.

∴小军在途中与爸爸第二次相遇时，距图书馆的距离为3000-2250=750（米）.

（3）当200x-1500-120x=100时，∴x=20；当120x-（200x-1500）=100时，∴x=17.5.

∴爸爸自第二次出发至到达图书馆前，20分钟或17.5分钟时与小军相距100米.

（4）当线段OD过点B时，小军的速度为1500÷15=100（米/分）；

四、表格信息题

例4某水果店在两周内，将标价为10元/斤的某种水果，经过两次降价后的价格为8.1元/斤，并且两次降价的百分率相同．

（1）求该种水果每次降价的百分率；

（2）从第一次降价的第1天算起，第x天（x为整数）的售价、销量及储存和损耗费用的相关信息如表所示．已知该种水果的进价为4.1元/斤，设销售该水果第x（天）的利润为y（元），求y与x（1≤x＜15）之间的函数关系式，并求出第几天时销售利润最大；

（3）在（2）的条件下，若要使第15天的利润比（2）中最大利润最多少127.5元，则第15天在第14天的价格基础上最多可降多少元？

时间x（天）售价（元/斤）销量（斤）储存和损耗费用（元）1≤x＜9第1次降价后的价格80-3x 40+3x 9≤x＜15第2次降价后的价格120-x 3x2-64x+400 x≥15

解析：（1）设该种水果每次降价的百分率是x，根据题意得10（1-x）2=8.1，

解得x=10%或x=190%（舍去）.

答：该种水果每次降价10%.

（2）当1≤x＜9时，第1次降价后的价格为10×（1-10%）=9，

∴y=（9-4.1）（80-3x）-（40+3x）=-17.7x+352，

∵-17.7＜0，∴y随x的增大而减小，

∴ 当x=1时，y有最大值，y最大=-17.7×1+352=334.3（元）；

当9≤x＜15时，第2次降价后的价格为8.1元，

∴y=（8.1-4.1）（120-x）-（3x2-64x+400）=-3x2+60x+80=-3（x-10）2+380，

∵-3＜0，9≤x＜15，∴当x=10时，y有最大值，y最大=380（元）.

第10天的销售利润最大.

（3）设第15天在第14天的价格基础上最多可降a元，由题意得

380-127.5≤105（4-a）-（3×152-64×15+400），

即252.5≤105（4-a）-115，解得a≤0.5.

答：第15天在第14天的价格基础上最多可降0.5元．

五、统计图表信息题

例5央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求，欲购进一批学生喜欢的图书.学校组织学生会成员随机抽取部分学生进行问卷调查，被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类，根据调查结果绘制了统计图（未完成），如图5所示.请根据图中信息，解答下列问题：

（2）将条形统计图补充完整；

（4）若该校共有学生2500人，估计该校喜欢“社科类”书籍的学生人数．

解：（1）此次调查的总人数为76÷38%=200（人）.

（2）喜欢生活类书籍的人数为200×15%=30（人），

∴喜欢小说类书籍的人数为200-24-76-30=70（人），

将条形统计图补充完整，如图6所示.

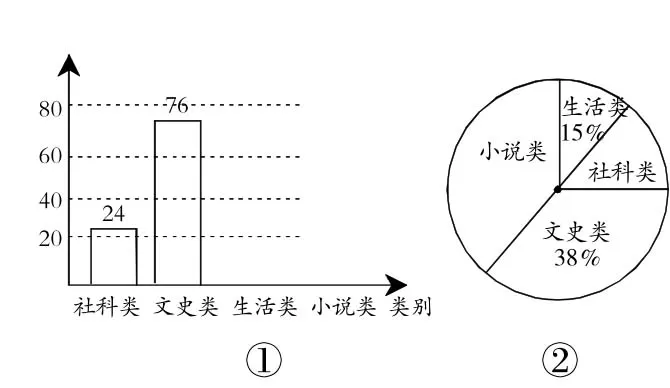
图5

∴喜欢小说类书籍的人数占总人数的百分比为100%-15%-38%-12%=35%，

∴小说类所在扇形的圆心角为360°×35%=126°.

（4）估计该校喜欢“社科类”书籍的学生人数2500×12%=300（人）.

图6