开放型题的归类解答

文/刘 顿

责任编辑：王二喜

开放型题能培养我们的创新思维能力，是近几年中考数学命题的一个新热点.开放型题可分为条件开放题、结论开放题、条件与结论开放题.请看下面的例子.

一、数与式中的开放题

例1三个代数式：①a2-2ab+b2；②3a-3b；③a2-b2.从中任意选择两个代数式构成分式，然后进行化简，并求当a=6，b=3时该分式的值.

分析：答案不唯一.

二、方程与不等式的开放题

例2一元二次方程x2-5x+c=0有两个不相等的实数根且两根之积为正，若c是整数，则c=.（只需填一个）

分析：∵一元二次方程x2-5x+c=0有两个不相等的实数根且两根之积为正，

∴Δ＞0，c＞0，即Δ＝（-5）2-4×1×c=25-4c＞0，

又∵c是整数，

∴c的值为1，2，3，4，5，6.

答案不唯一.如填1.

三、函数开放题

分析：答案不唯一.只要k＜0就符合题意.

四、三角形与四边形的开放题

例4正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A按顺时针方向旋转，记旋转角∠DAG=α，其中0°≤α≤180°，连接DF，BF，如图1.

（1）若α=0°，则DF=BF，请加以证明；

（2）试画一个图形（即反例），说明（1）中命题的逆命题是假命题；

（3）对于（1）中命题的逆命题，如果补充一个条件后，能使该逆命题为真命题，请直接写出你认为需要补充的一个条件，不必说明理由.

图1

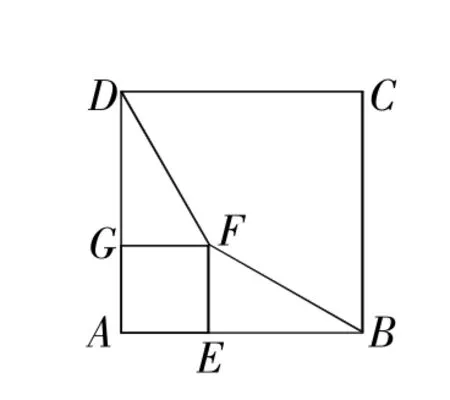
图2

图3

分析：（1）如图2，∵四边形ABCD和四边形AEFG为正方形，

∴AG=AE，AD=AB，GF=EF，∠DGF=∠BEF=90°，

∴DG=BE，

∴△DGF≌△BEF，∴DF=BF.

（2）图形（反例），如图3.

（3）答案不唯一.

如，F在正方形ABCD内，或α＜180°，若点F在正方形ABCD内，DF=BF，则旋转角α=0°.

五、圆与相似形的开放题

例5如图4，OB是已O的半径，弦AB=OB，直径CD⊥AB，若点P是线段OD上的动点，连接PA，则∠PAB的度数可以是（写出一个即可）.

分析：不妨设AB与CD交于点E，

∴∠BOE=30°，∠OBE=60°.

当点P与点O重合时，∠PAB=∠OAB=∠OBA=60°；

当点P与点D重合时，连接OA，则∠OAB=60°，∠AOC=30°，

∵OA=OD，∴∠ODA=∠OAD=15°，∠PAB=75°，

当点P在线段OD上移动时，60°＜∠PAB＜75°.

故答案不唯一.

如，∠PAB的度数可以是70°.

图4

六、统计与概率的开放题

例 6 已知A组数据如下：0，1，-2，-1，0，-1，3.

（1）求A组数据的平均数；

（2）从A组数据中选取5个数据，记这5个数据为B组数据.要求B组数据满足两个条件：①它的平均数与A组数据的平均数相等；②它的方差比A组数据的方差大.

（2）答案不唯一.

A组数据的平均数为0，B组数据的平均数也为0，去掉的2个数的和为0即可.

如，选取的B组数据是：1，-2，-1，-1，3.

所以数据1，-2，-1，-1，3符合题意.