矩阵A的特征值与特征向量的关系理论研究及应用

贺加来

（合肥职业技术学院，安徽 巢湖 238000）

1 引言

特征值与特征向量是高等代数中的两个重要概念，大多数教材中介绍其如何求法，对特征值与特征向量的关系没有深入介绍。通过两者的概念深入研究两者的关系，得到有关的结论，为读者提供有益的帮助。

2 特征值与特征向量的关系研究

假定 λ1，λ2，…λm是 A 的 m 个不同特征值，X1，X2，…Xm是分别与它们对应的特征向量，即

这些特征向量彼此之间的关系如何呢？

假定 c1X1+c2X2+…+cmXm=0

用矩阵A去左乘，再用（1）式代入即得：λ1c1X1+λ2c2X2+… +λmcmXm=0

同样再用A左乘，用（1）式代入继续这样做，一般得：

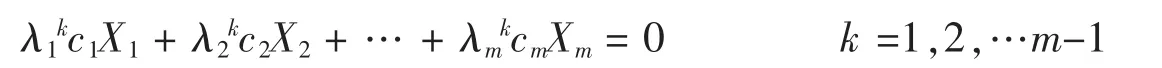
于是有m个向量的齐次线性方程组：

所以D≠0，引用克莱姆法则得到：ciXi=0

但Xi是A的特征向量，所以Xi≠0，因此ci=0，这就证明了下面的定理：

定理1：对应于矩阵A的不同的特征值的任一组特征向量是线性无关的。

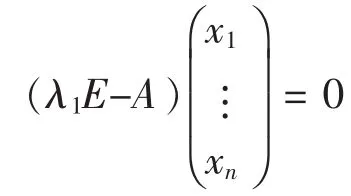
对于特征值λ1的所有特征向量和零向量都是齐次方程组

的解向量，所有这些解向量形成n维空间Rn的一个k维子空间S，称之为A对于λ1的特征子空间，这时（λ1E－A）的秩是 n-k。

现假设 X1（1），X2（1），…Xk（1）是（3）的一组线性无关的解向量，当然，

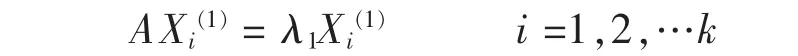
再选取 n-k 个向量

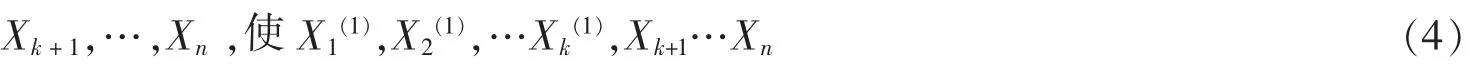
成为 Rn的一组基，作 n 阶矩阵 P= （X1（1），X2（1），…Xk（1），Xk+1…Xn）其中第一、第二，……第 n 列向量顺序是（4）中的向量，于是P是满秩的，根据矩阵乘法规则，得：

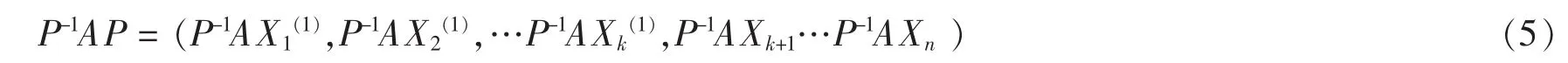
但 AXi（1）= λ1Xi（1），因此 P－1AXi（1）= λ1P－1AXi（1）i=1，2，…k

又由于 E ＝ P－1P= （P－1X1（1），P－1X2（1）… P－1Xk（1），P－1Xk＋1，…P－1Xn）

即得 P－1Xi（1）是单位阵 E 的第 i列，所有（5）式可以写成

式中的B1是n-k阶矩阵，O是（n-k）×k矩阵，*表示k×（n-k）矩阵，由拉普拉斯定理得：

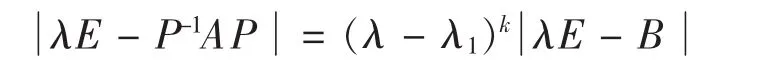
但

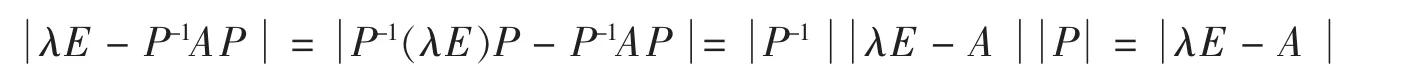
所以

这就是说λ1至少是A的k重特征根，因此得到并证明了下面定理：

定理2：矩阵A对应特征根λ1的特征子空间的维数不超过λ1在△A（λ）中的重数。特别又得到了：

推论：矩阵A的特征多项式的单根所对应的特征子空间的维数等于1。

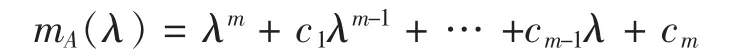
那么

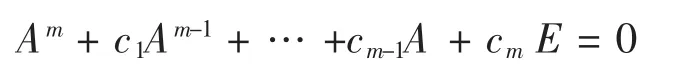
但

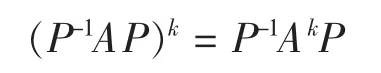
所以

这就是说，mA（B） ＝ 0 式中 B=P－1AP，因之 mB（λ） /mA（λ）

同理 mA（λ） /mB（λ），所以 mA（λ）＝ mB（λ），于是得到了：

定理3：相似矩阵有相同的特征多项式和相同的最小多项式，因而有相同的特征值和相同的迹，即

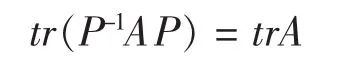
在研究有相同的特征多项式的矩阵时，进一步研究一个问题，那就是AB和BA的特征多项式问题。

假如A、B中有一个是满秩，如A是满秩，由于BA=A-1ABA，所以AB和BA相似，因此有定理3得知AB和BA有相同的特征多项式。

更一般情形，因A至多有n个不同的特征值，所以有一个实数t0存在，使凡适合t＞t0的t都有即A-tE是满秩的，于是（A-tE）和B（A-tE）有相同的特征多项式，即

对于任何 t＞ t0都成立，把（6）改写成

两边对每个固定的λ值是两个关于变量t的多项式，当时t＞t0，它们的值相等，于是这两个t的多项式是恒等的，因之以t=0代入即得：

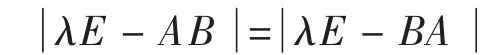
定理4：假定A、B是两个n阶矩阵，那么AB和BA有相同的特征多项式，因此有相同的特征值和迹，即 tr（AB） =tr（BA）。

3 结论的应用

已知 A 与 B 相似。（1）求 a与 b；（2）求可逆矩阵 P 使 P－1AP=B。

解：由定理3得：

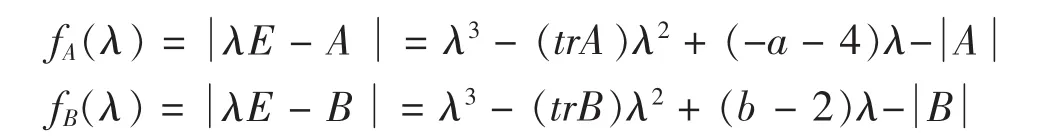
由 fA（λ） =fB（λ）得

即 a-b=2，-a-4=b-2，

解得a=0，b=-2

（2）由于A与B相似，所以A的特征值与B的特征值相同，就是B的对角元，λ1=-1，λ2=2，λ3=-2，再求出对应于这些特征值的特征向量分别是：

则有P-1AP=B。

解题过程表明，此解法优于传统方法。