欧式空间正交基函数及其应用

唐桂林 陈明武 郭清伟

（1 安徽邮电职业技术学院，安徽 合肥 230031）（2 合肥工业大学，安徽 合肥 230009）

1 引言

线性空间是线性代数最基本的概念之一，也是我们碰到的第一个抽象的概念，在线性空间中，向量之间的基本运算只有线性运算，即加法运算和数量乘法运算，如果我们以几何空间中的向量作为线性空间理论的一个模型，那么就会发现向量的度量性质如长度、角度等在线性空间的理论中没有得到反映，但向量的度量性质在许多问题中有着特殊的地位。而在解析几何中，向量的长度与夹角等性质都可以通过向量的内积来表示，所以在本文中，我们根据内积的定义构造欧式空间的基函数，为后续研究欧式空间曲线、曲面打下夯实的基础。

近年来欧式空间被众多学者广泛的研究，孙维君欧式空间中向量的叉积及其应用[1]，杨秀娟欧式空间中反向最远邻查询方法的研究[2]，张锦来欧式空间上的变换是线性变换的充分条件[3]。劳毅慧欧式空间的一个推广[4]。孙侠常见线性空间与欧式空间的基于标准正交基的求法[5]等，文献中[6-18]讨论了Bernstein基函数的对偶基及其应用，特别是在多项式曲线降阶和升阶方面的应用；文献[19]主要讨论了一般多项式基函数的对偶基问题；文献[20]给出了任意类型基函数的对偶基的构造方法，该方法也需要解一个线性方程组才能得到对偶基，但与已有方法相比，其计算量由O（N3）变为O（N）。

2 欧式空间的定义

定义1[21]：

设V是一个非空集合，ρ是一个数域，在集合V的元素之间定义了一种运算，叫做加法；这就是说，给出了一个法则，对于V中任意两个元数素α与β，在V中都有唯一的一个元素，γ与它们对应，称为α与β的和，记为γ=α+β。在数域ρ与集合V的元素之间还定义了一种运算叫做数量乘法，这就是说，对子数域ρ中任一数k与v中任一元素α在V中都有唯一的一个元素与它们对应，称为kα的数量乘积，记作σ=kα若加法和数量乘法满足下述规则那么V称为数域ρ上的线性空间。

定义2[21]：

设v是实数域R上的线性空间，对V中任意两个向量α，定义一个二无实函数，记作〈α，β〉，若〈α，β〉满足以下性质：∀α，β，γ∈v，k∈R

则称〈α β〉为 α 和 β 的内积

定义3[21]：

定义了上述内积的实数域上的线性空间称为欧式空间。

3 欧式空间的内积

定理1[21]：

C[a，b]为闭区间[a，b]上的所有实数连续函数所作成的线性空间，f（x），g（x）是定义在[a，b]上的连续函数，对 f（x），g（x）若满足

则 C（a，b）对于（1）作成一个欧式空间。

4 构造欧式空间的正交基函数

定理2[21]：

对于 n维欧式空间中任意一组基函数 ε1，ε2，…εn都可以找到一组标准正交基 η1，η2，…ηn满足：

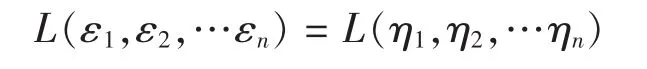
定理3：

定理4：

设 1、cosx、sinx 、cos2x、sin2x、…cosnx、 sinnx....是定义在闭区间[0，2π]上的连续函数，其所作成的空间为欧式空间。其中1、cosx、sinx、cos2x、sin2x、…cosnx、sinnx…为该欧式空间的一组基函数。

证明：对于基函数 1，cosx，sinx，cos2x，…，cosnx，sinnx，…中任意两个基函数都满足以下性质

即符合内积定义

所以 1，cosx sinx，cos2x，sin2x，…cosmx.sinmx 构成欧式空间一组基函数。

定理5：

欧式空间基函数 1、cosx、sinx、cos2x、sin2x、…cosnx、 sinnx…是一组线性无关正交基

证明：当m≠n时，根据定理3中的结论，则有

即该组基函数是正交基函数；为了方便表示我们分别用η1，η2，…ηm…表示欧式空间基函数1，cosx、 sinx，…cosmx、sinmx…

下面我们证明正交向量组 1，cosx、sinx，…cosmx、sinmx、…线性无关：

设正交基函数存在线性关系

分别用基函数 1，cosx、sinx，…cosmx、sinmx、…与上述等式作内积（定理 1）运算，即得：

由于（sin mx，sin mx） ＝ π，所以 ki=0，i=1，2，3 ，…

即 1，cosx、 sinx，…cosmx、sinmx、…线性无关。定理证毕。

5 欧式空间基函数的对偶基及其升阶算法

定理6：

设 e0，e1，…，en是一组线性无关的基函数，其生成空间为 En，即其对偶基函数为｝可以表示成 e0，e1，…，en的线性组合。即

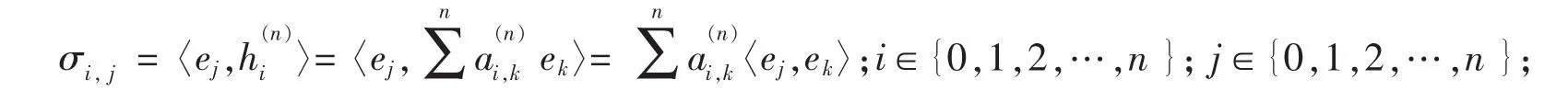
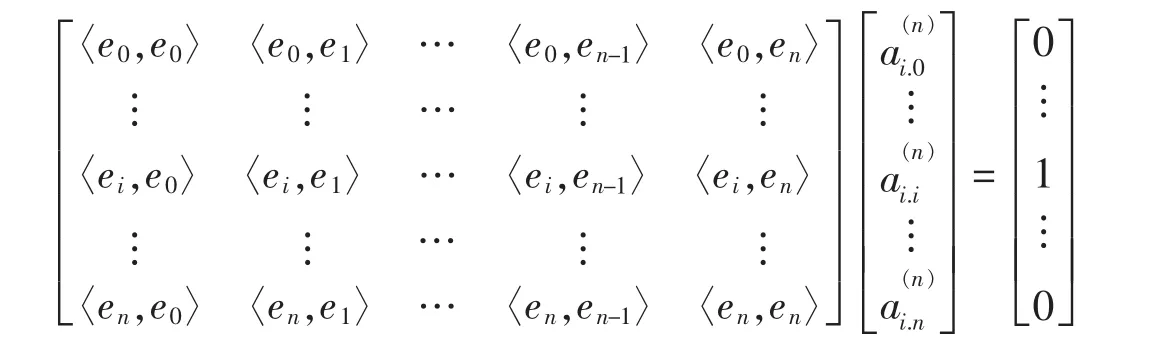
即

定理7：

Em对偶基函数为对偶基空间为

即

即有：

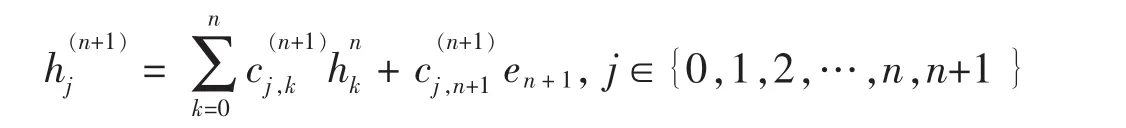
根据对偶基的定义则有

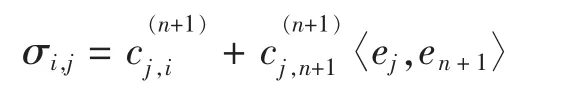
当 i=n+1；时

即

其中

6 举列

（1）当 i＝ 0 时

即根据对偶理论

即

系数矩阵A是实对称矩阵，利用matlab编程可以得到

即

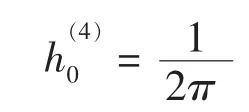
（2）当 i＝ 1时，同理可有

（3）当 i＝ 2时，同理可有

（4）当 i＝ 3时，同理可有

（5）当 i＝ 4时，同理可有

综合上述：得到 e0=1，e1=cosx，e2=sinx，e3=cos2x，e4=sin2x的对偶基函数分别是

下面我们进一步讨论其升阶算法：

根据定理7，我们现在利用欧式空间E4基函数的对偶基H4求解E5基函数的对偶基函数H5，其中，

若 j=0 时下面分别讨论 i=0，1，2，3，4，5 时的情况

（1）当 i=0 时即

（2）当 i=1 时即

（3）当 i=2 时即

（4）当 i=3 时即

（5）当 i=4 时即

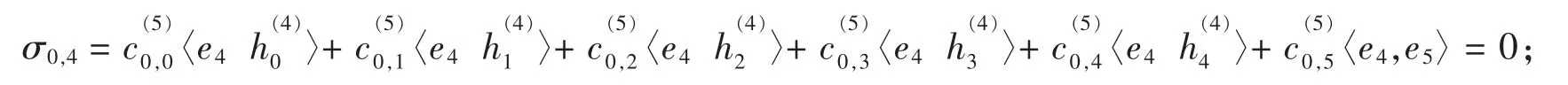
（6）当 i=5 时即

当j=0时可以得到矩阵M如下：

故有：

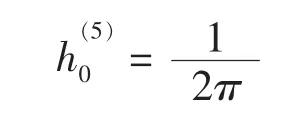
即

同理可求：

7 结论

由于欧式空间的应用越来越广，国内外许多学者都利用范数、内积来研究欧式空间，本文根据泛函分析中内积的定义、基函数的定义构造欧式空间的基函数，并证明该基函数是欧式空间的正交基函数。对后续研究欧式空间曲线、曲面有着重要意义。