PageRank算法的二级加速优化方案

刘健雄，王晓程，毛俐旻

(1.中国航天科工集团二院研究生院，北京 100854；2.中国航天科工集团二院706所，北京 100854)

0 引 言

本文将讨论当今最具研究价值的主流网页排序算法——PageRank算法，并对其进行改进。本算法由Larry Page和Sergey Brin提出，其思想是通过分析网络的链接结构来获得网络中网页的重要性排名，且该算法已应用于Google搜索引擎[1]，成为其评价网页好坏的唯一标准。不过，该算法的执行速度和资源损耗等方面已无法适应当今信息爆炸的时代特性，所以如何更有效更快速地提升该算法的运行效率成为研究该算法的重中之重。

如今对于PageRank算法优化研究多种多样，可从改善网络图结构、加快算法收敛速度、实现算法并行化等各种角度提高算法效率。Héctor Migallón等利用启发式松弛外推法对原算法中幂法实施加速[2]；Lanying Li等利用TopK算法删除网络图冗余节点得到优化子图进行网页评估[3]；Arne Koschel等利用Hadoop分布式计算网络图节点值[4]。上述各方案均对PageRank算法的某一方面进行单次加速，加速效果有待提升。

本文将通过多级加速幂法迭代收敛的方式继续提升PageRank算法的执行效率。其中，原点平移法和Aitken加速算法已被证明为加速幂法收敛的有效方法，所以本文将提出一种基于以上方法的二级加速优化算法，通过仿真实验分析该方案的加速效果，并且原理上可与算法并行化等其它优化方案相结合，拥有更高的普适性、可行性，从而达到完善PageRank算法优化的目的。

1 PageRank算法研究

1.1 算法原理

PageRank算法基于网页的入链数量和网页质量两方面进行分析计算[5]，即一个网页接收到其它网页指向的链接越多，或指向它的网页的质量越高，则该网页越重要，PageRank值越高。使页面i的PageRank值由PR(i)表示，则最终PageRank表达式为

(1)

其中，p1，p2,…,pN为所有被研究的页面，q为阻尼系数，L(pj)为页面pj链出页面的数量，N为所有被研究页面数量。

PageRank向量代表用户在任意特定网页中随机点击链接所到达页面的概率分布。经修正后的网页相互链接状态所构建的概率矩阵满足马尔科夫矩阵特性，故而求解Page-Rank向量的过程即为计算该概率矩阵最大特征值所对应特征向量的过程。而通过幂法计算已被证明为解决该问题最有效的方式。所以，本文将针对幂法计算这一过程进行加速，从而达到优化整个PageRank算法的目的。

1.2 应用幂法求解

幂法是一种计算矩阵主特征值(即矩阵按模最大的特征值)及相应特征向量的迭代方法，尤其适用大型稀疏矩阵。因此，当下搜索引擎应用PageRank算法进行网页排序时，多应用幂法进行计算PageRank向量。

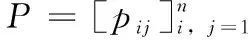
(2)

即迭代向量。则最终可推导出

(3)

利用式vk+1=Pvk不断进行迭代，直到vk+1与vk值近似时停止，此时vk即为符合精确标准的所求特征向量近似值。其中所需迭代次数越少表明幂法收敛速度越快，整体PageRank算法的处理数据效率越高。

现有PageRank算法的优化方案多仅对幂法计算进行一次加速，优化效果有待提升，因此，本文将对幂法计算实施二级加速，首先对原始矩阵进行预处理，得到计算起来收敛更快的等效矩阵；再对等效矩阵的幂法计算应用改进的Aitken算法进行加速，并通过实验验证加速两次的效果比现今多数类似优化方案加速效果更明显。

2 基于原点平移法的一级加速方案

原点平移的加速方法是一种矩阵变换方法，将原始矩阵转化为计算主特征值时收敛速度更快的等效矩阵，从而实现加速。将该方法应用到PageRank算法矩阵的计算中，不会破坏原矩阵的稀疏性，同时依然可以应用其它加速算法继续加速幂法收敛，相互结合使用，从而达到多级加速的效果。

该方法核心在于引进等效矩阵B=P-bI，其中b为选择参数，矩阵I为单位矩阵。原矩阵P的特征值为λ1，λ2，…，λn，则矩阵B相应的特征值为λ1-b，λ2-b，…，λn-b，同时矩阵P与B的特征向量相同。若计算矩阵B特征向量时的收敛速度比矩阵P的快，即可达到预想的加速效果。

首先，由上式(4)可知

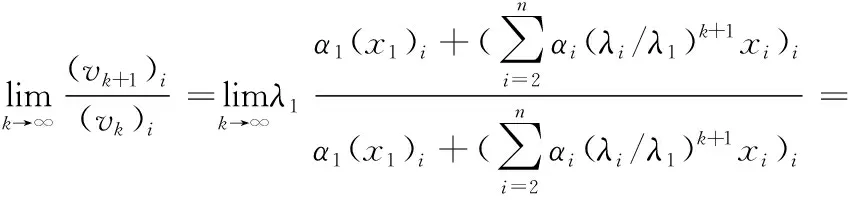
(4)

其中，(vk)i表示向量vk的第i个分量。(vk+1)i/(vk)i→λ1的收敛速度由比值r=|λ2/λ1|确定，r越小收敛越快，当r=|λ2/λ1|≈1时，收敛将十分缓慢[6]。

因此，在保证选择参数b使λ1-b仍然是矩阵B的主特征值的同时，还应满足

(5)

即计算矩阵B主特征值对应的特征向量时的收敛速度比计算矩阵P时的要快。

由于矩阵P的特征值满足|λ1|>|λ2|≥|λ3|≥…≥|λn|，且当特征值为正时，则λ1>λ2≥λ3≥…≥λn，因此矩阵B=P-bI的主特征值必为λ1-b或λn-b。当求矩阵P的特征值λ1对应的特征向量时，则b首先应满足|λ1-b|>|λn-b|，同时收敛速度的比值尽量最小，即

(6)

所以，当(λ2-b)/(λ1-b)=-(λn-b)/(λ1-b)，即b=(λ2+λn)/2时，收敛速度的比值最小，收敛最快。

需要注意的是，真实网络邻近矩阵P的特征值不一定均为正，增加了选取合适b值的难度，只有通过对网络矩阵分布的了解来粗略地估计最佳b值的相似值，依然能进行加速收敛，同样可大量减少处理真实网络庞大数据的时间。另外，预估b值首先需要预估出矩阵P的λ2、λn值，这也增加了许多处理数据的计算量。当下信息极速膨胀，热点实时更新，网页的相互引用关系不断变化，导致一段时间需重新预估矩阵P的λ2、λn值，进一步削弱了该方案的加速效果。

可以看出，基于原点平移法的一级加速方案具有一定的局限性，实际加速效果仍需实例仿真进行验证。因此，在我们将矩阵P预处理转化为等效矩阵B后，还需进一步优化计算过程，对收敛过程实施二级加速。

3 Aitken加速算法研究

Aitken加速算法是一种提高迭代法收敛速度的有效算法。该方法应用弦截法根据已迭代计算出的值来获取新的近似迭代值序列，且新序列的收敛速度比原序列要快，从而达到加速收敛的效果。因此，研究该算法并在此基础上进行改进，是提高PageRank算法效率的重要途径。

由式(3)可知，vk为主特征值对应的特征向量x1的近似值，并且每迭代一次，vk越趋近于x1的精确值。应用迭代公式迭代一次可得vk+1=φ(vk)，继续迭代可得vk+2=φ(vk+1)。应用微分中值定理，有vk+1-x1=φ(vk)-φ(x1)=φ′(ξ)(vk-x1)，其中φ′(ξ)变化微小，可粗略近似为定值[7]，因此，将多式联立可推导出

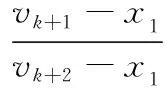
(7)

进而

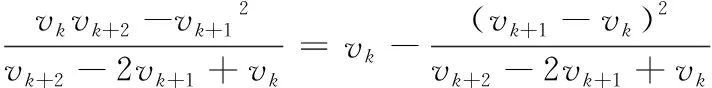
(8)

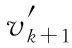
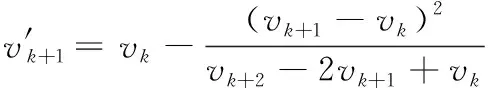
(9)

4 基于改进Aitken算法的二级加速方案

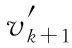
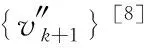
(10)

(11)

下面给出理论证明

比较两序列(9)、(10)，则有

(12)

从而推出

(13)

所以

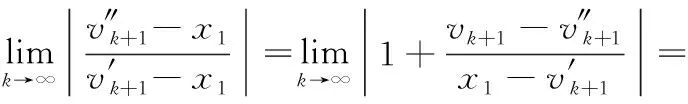
由上式可得出，改进的Aitken加速算法比标准算法收敛速度更快，因此，对于整个PageRank算法的执行效率提升更大。综合上文所述两种加速方案，则可看出该二级加速方案比现有类似的优化方案加速效果更加明显，且可与并行化等其它方案结合使用，更具实际操作价值。

5 二级加速优化方案实现

5.1 方案描述

(1)矩阵公式化真实网络网页链接状态，得到网络图邻近矩阵G=[gij]i,j=1。

(2)构建矩阵G的跃迁矩阵P，其中pij=gij/ci，再加入阻尼系数q，对矩阵P进行修正，得到最终矩阵P=qP+(1-q)eeT/N。

(3)引进选择系数b，将矩阵P进行原点平移，得到加速矩阵B=P-bI，通过计算加速矩阵B主特征值所对应的特征向量，得到矩阵P相应的特征向量。

(4)利用幂法计算矩阵B主特征值对应的特征向量，其中应用改进的Aitken算法加速幂法计算中的收敛速度，即可得到矩阵P相应的特征向量，从而求得各网页的Page-Rank值[9,10]。

下面给出该算法的伪代码：

Function ImprovedPowerMethod( ) {

Initialize(v0);

B=P-bI; //矩阵预处理

k=1;

while(error>=ε){

vk=Bvk-1;

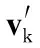
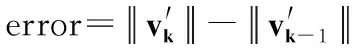
k=k+1;

}

}

5.2 实例仿真

实际搜索引擎处理网页排序的规模十分巨大，例如Google的存储网页数量已到109级别，由于硬件条件限制，本文拟选用较小规模的web网页链接情况进行测试[6]。以下提供的链接情况来源于网络爬虫抓取的固定站点(sogou.com)内的10 000条链接。由于固定站点内网页相互链接频繁，可避免大量的孤立网页存在，提高本实验的普适性。另外，为了体现本文提出的改进算法的效果，将阻尼系数q设为0.99，尽量减少该系数对收敛效果的影响，从而更能体现改进算法的作用。

图1测试所应用计算机参数为内存6 GB，处理器Core i5-4200U，主频1.60 GHz，测试矩阵为基于上述抓取网页链接所构成的10 000*10 000矩阵，将选择参数b分别设为0.1、0.3、0.6，得到3个预处理后的等效矩阵，使用标准幂法分别计算原矩阵及以上3个矩阵，得到各矩阵幂法计算的收敛曲线并进行比较。

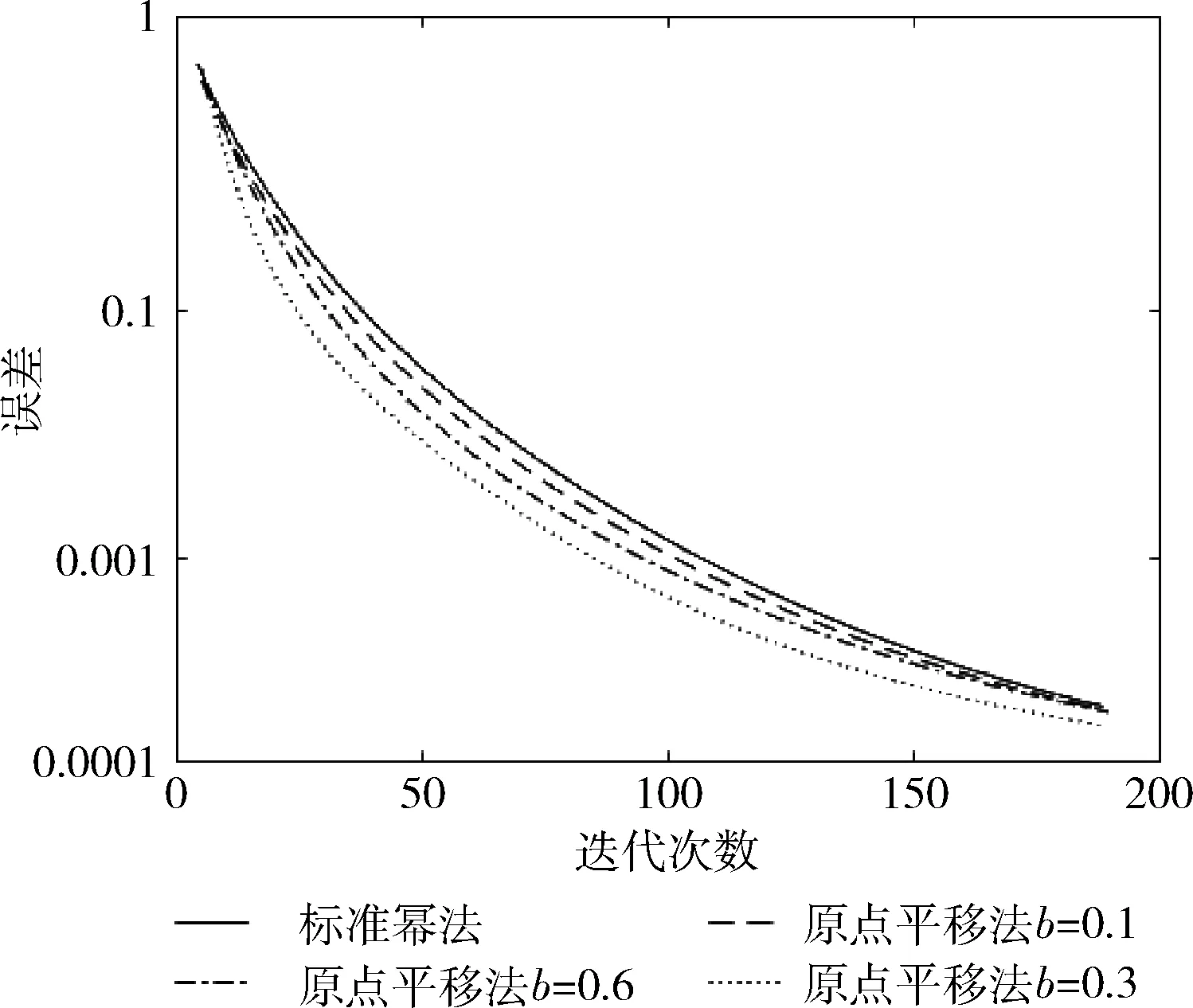
图1 测试结果1

由图1可看出，利用原点平移法得到的等效矩阵幂法计算时收敛速度有所增加，当选择系数b取不同值时，加速效果不同。当b=0.3时，加速效果最明显，即当迭代50次时的误差和标准幂法迭代70次时的误差相近，提高效率近40%；当b=0.1时，则曲线基本重合，提高效率近8%。因此，选择系数的选取对于该方案的加速效果至关重要。

图2显示分别使用传统Aitken算法和改进的Aitken算法来计算该矩阵的特征向量时的收敛曲线，其中硬件条件及被测矩阵与图1实验相同。

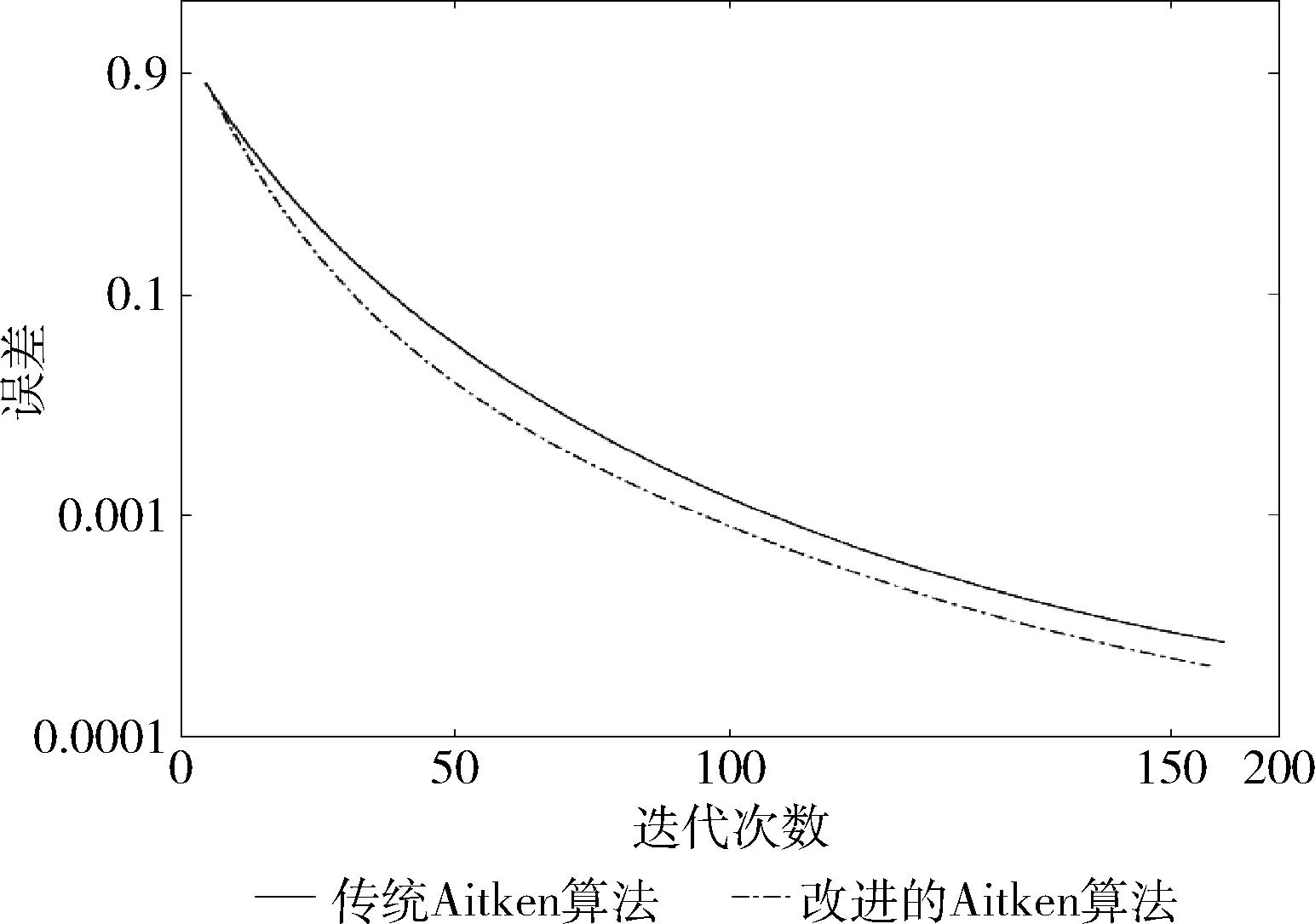
图2 测试结果2

由图2可看出，改进的Aitken算法收敛速度较传统算法收敛速度略有提高[9]，其中改进算法在迭代50次时的误差和传统算法迭代65次时的误差相近；迭代75次时的误差和传统算法迭代93次时的误差相近；迭代100次时的误差和传统算法迭代120次时的误差相近，可计算出改进的Aitken加速算法分别提高了30%、24%，20%左右的效率，可知改进后算法迭代初始时加速效果明显，到迭代后期趋于平缓，根据日常迭代需求，可大致估算出该改进算法提高效率在25%左右。

图3显示分别使用标准幂法、本文提出的改进算法以及某启发式松弛外推法[2]加速的幂法计算该矩阵最大特征值1对应的特征向量的收敛曲线，其中硬件条件及被测矩阵与图1实验相同，所引用其它优化方案根据所引文献中给出的核心算法编写大致程序。

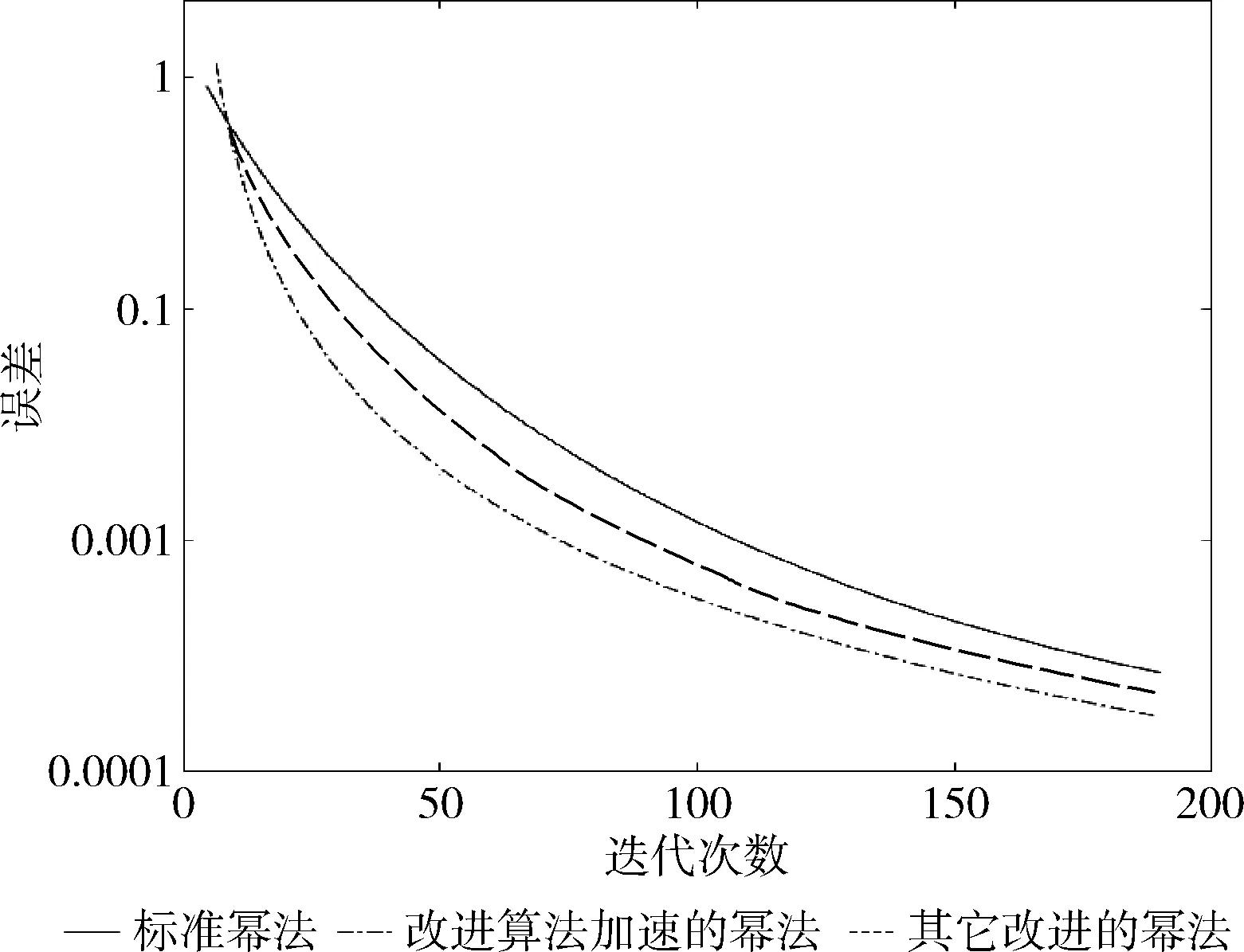
图3 测试结果3

由图3可看出，相对于原PageRank算法，应用本文提出的改进算法加速后的幂法收敛速度大大提高，其中改进算法加速后的幂法在迭代50次时的误差和标准幂法迭代80次时的误差相近；迭代75次时的误差和标准幂法迭代120次时的误差相近；迭代100次时的误差和标准幂法迭代150次时的误差相近，可计算出改进后的幂法分别提高了60%、60%，50%左右的效率，可知改进算法加速效果明显，基本稳定在60%左右的加速效率。另外，在实际计算中，计算机的内存使用率一般在40%左右，改进算法的内存损耗略高但并不明显，可以忽略。相对于所比较的某启发式松弛外推法，本文提出的改进算法对于幂法收敛速度的加速效果略为显著，其中本文改进算法加速后的幂法在迭代50次时的误差和其它改进算法加速后的幂法迭代55次时的误差相近；迭代75次时的误差和对比的幂法迭代80次时的误差相近；迭代100次时的误差和对比的幂法迭代110次时的误差相近，可计算出改进后的幂法分别提高了10%、6.67%，10%左右的效率，可知本文改进算法相比于类似其他优化方案加速效果略有提高。

6 结束语

PageRank算法作为当今搜索引擎中网页排序的主流算法，其本质是求解网络邻近矩阵最大特征值对应的特征向量，而幂法则是解决该问题最有效的方法[10]。因此本文主要针对幂法计算提出了一种二级加速优化方案，并在小规模真实网页抓取过程中测试该方案的性能，实例验证了该方案的加速效果明显。不过，基于原点平移法的一级加速程序优化效果受原矩阵元素分布的影响较大，在处理大规模网页数据矩阵过程中，系数的选择和加速的效果方面同样待验证。所以，仍需对此进行更全面深入的研究，并设计更完善稳定的加速程序。另外，在改进Aitken算法方面，也有进一步提升加速效果的空间。