促销策略角度下允许缺货的两层库存模型规划

陈香堂 ，马卫民，孙秉珍

（1.同济大学 经济与管理学院，上海 200092；2.温州职业技术学院 工商管理系，浙江 温州 325035；3.西安电子科技大学 经济与管理学院，西安 710071）

随着商品经济与网络经济的快速发展，及时适应消费者的需求以及迅速做出市场反应已经成为市场竞争的有力武器。保持适量库存以获取竞争优势是经常采取的一种策略，因此，库存系统的管理已经成为非常重要的管理问题。零售商经常要解决订货时间和订货批量这两个基本问题。为了达到收益值最大化的目的，一般要综合考虑产品的制造成本、库存成本和订货成本等因素。此类问题的经典解决思路是运用Harris的经典经济批量模型（EOQ）。经典EOQ 模型的基本假设是不允许缺货、库存能够得到及时补充的情况。经典EOQ 模型认为缺货将导致产品脱销而丧失了销售机会，Zipkin[1]讨论了缺货情况，并将其推广至经济生产批量模型（EPQ）。随后，不同学者深入研究了缺货情况，并认为现实中有些顾客愿意继续等待，有些则不会。对于是否含有缺货变量的模型最早出现在Fabrycky等[2]以及Ali[3]的研究中。Montgomery等[4]给出了此类问题的解决方法。现实商业运作中经常出现缺货状态，而不允许缺货的假设在一定程度上限制了EOQ 模型的应用范围。因此，很多学者从多个角度系统研究了允许缺货的库存问题。Deb等[5]是其中具有代表性的研究之一，其从允许缺货的角度拓展了已有模型。其他学者在该拓展模型基础上进行了一系列深入研究[6]。

众所周知，在现实的商业操作中，由于市场位置的租赁成本较高，故零售商会在店面内开发出一个储存少量产品的小仓库。为了配合促销策略产生的大量销售或在市场需求量较大时，零售商订货量超过小仓库的容量也许能获得更大的收益。考虑到销售的便利性、降低产品成本以及降低销售机会成本等目的，一些销售商采取同时拥有店面库存仓库和租赁库存仓库两个库存仓库的策略。

然而，在某些具体的现实情境和具体的操作实践中，另外租赁仓库对于零售商并不一定是盈利的，特别是租赁仓库成本很高时。此时必须考虑如下问题：零售商坚持一个店面仓库还是再租赁第2个仓库。一些学者分别从无限补货率和有限补货率的角度研究了双层库存模型；而另一些学者则从市场需求角度提出了双层库存模型。Hartley[7]研究了两层仓库模型。Zhou等[8]考虑运输成本，建立了存货和市场需求相互独立的双仓库库存模型。在充分考虑现实问题具体特征的基础上，针对双层仓库库存模型[9-11]的研究是近年来较为有代表性的研究。

在市场竞争日益加剧的情形下，促销措施已经成为商业运作的重要策略。一方面，促销措施有助于新产品的推出、延长产品的生命周期、扩大产品的市场占有率。促销措施一般包括免费礼物、折扣优惠、配送便利、更好的服务和广告等措施。另一方面，促销措施的实施必然会引起市场需求的变化，从而影响库存的管理策略。Goyal等[12]研究了不同促销措施影响产品市场需求的多阶段生产体系中的经济订货批量，并给出了整合的生产-库存-市场模型。Nair等[13]研究了免费礼物、价格折扣和特殊服务等方式形成的促销效果对库存的影响，并对此进行了优化设计。Krishnan等[14]的研究结论证明了价格优惠、产品展示、免费物品和广告是获得最大收益的基本策略。Sun[15]研究发现，顾客和不同促销类型存在一定关系，特别是促销措施强化了品牌对顾客行为的影响。另一些学者从数量折扣、价格折扣以及延期支付等角度研究了库存管理的优化策略[16-18]。Sana等[19-24]从影响需求的企业动机、销售人员动机和允许缺货等角度研究了EOQ 模型。

尽管对于两层库存规划问题的研究获得了较多成熟且系统的研究模型和方法，并获得了诸多有价值的研究结论；但是关于两层库存规划的研究和对于考虑促销策略影响市场需求变化情况[24]的研究尚不多见；同时，目前针对允许缺货的促销策略情景下的库存规划的研究中亦很少有结合两层库存的相关研究[11]。现实中，允许缺货、促销策略的实施和两层库存已经成为现实商业运作中的常态[11]，为了更好地解决现实中出现的问题，本文考虑在允许缺货的约束下，从促销策略影响市场需求的角度研究两层仓库库存系统，讨论如何确定促销措施的力度以及最优的缺货量，进而制定订货批量最优策略，最终实现库存系统收益的最大化。

1 数学模型的构建

考虑到市场需求受促销策略的影响以及双层库存系统与单层库存系统之间的差异，本文从促销策略影响市场需求、双层库存之间联系以及决策变量等方面进行一些合理的模型假设，详细说明模型所需的符号及参数，并在此基础上建构目标函数。

1.1 模型假设

为便于模型的建立，作如下假设：

（1）生产商产能有限，允许缺货。最优订货量和允许缺货量同时决策。

（2）零售商有两个库存仓库，分别为店面库存仓库OW（Own Warehouse）和租赁库存仓库RW（Rented Warehouse），店面库存仓库位于店面内部，租赁库存仓库位于离店面不远处。管理人员经常检查库存情况，保证店面库存仓库OW 的库存水平充足。若仓库OW 货源不足，将及时、持续地从RW补货。OW 的库存下降到某一水平库存时，发出补货指令，且补货及时。货物到达后，先解决缺货问题，再补充OW 库存至充足水平，余下货物最后运往RW 保存。OW 至RW 之间的运输成本忽略不计。

（3）促销策略将在很大程度上促进商品的市场需求，市场需求率是关于促销因子的函数，即D=x⊕d（ρ）[24]，一般常数x＞0。⊕表示“+”或“×”的运算符号，这将根据商品的特点、市场竞争情况与促销策略之间的关系而定。此外，假设ρ为促销因子，反映了促销策略所产生的市场需求效果，该因子可促进商品的市场需求增加。而，其中τ为常数，一般地，τ＞0。

（4）店面主要用于商品的正常经营，在保证店面正常经营所需的必要场所外，利用剩余不多的店面空间开发店面仓库（OW）。OW 的库存不超过OW 的库存容量，库存不影响店面的正常经营，可认为在固有经营模式下店面大部分成本主要用于支付店面经营的租金，属于商品的经营成本。此时，OW 的库存容量为有限，且不影响店面的正常经营[11]。

1.2 符号说明及参数

本文建模设计参数：

D——每年市场需求率

q——每周期订货量

s——每周期缺货数量

c2——RW 的单位库存成本

c22——OW 的单位库存成本

c1——每次订货成本

p1——单位产品的购买成本

s1——单位产品销售价格

c3——单位缺货成本

k——促销成本的比例参数

kρm——促销成本

w——OW 的库存容量

m——促销成本的弹性参数，m∈Z+

Z——本文的收益函数

T——周期时间

Z24——文献[24]的收益函数

1.3 目标函数的建立

在时间0到时间t1，库存量由（q-s）减少至w，此时RW 库存为0。再经过时间t2，库存量为0，此时OW 库存为0。t3为缺货时期。周期时间T=t1+t2+t3。上述库存变化情况如图1所示。

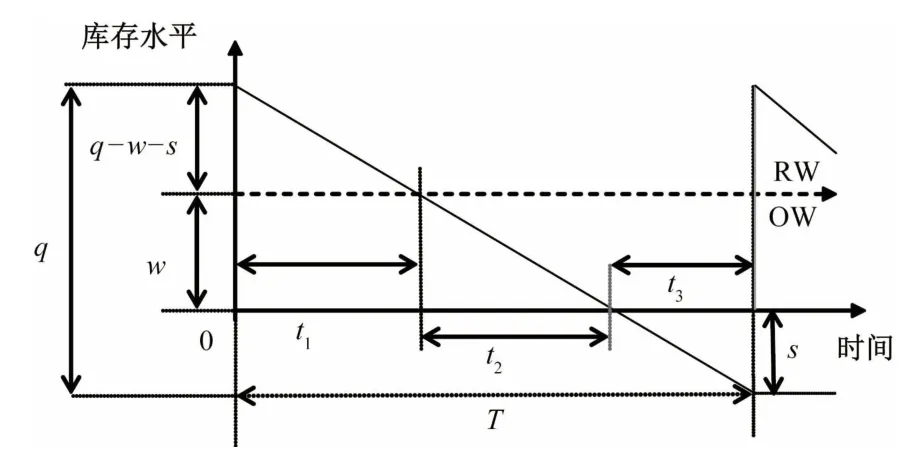
图1 OW-RW 库存变化图

考虑到收益与销售收入、订货成本、库存成本、缺货成本和促销成本有关，因此，收益函数模型为

根据上述假设和分析可知，由于每周期订货量和每周期的缺货数量与市场需求率相关，市场需求率是关于促销因子的函数，故每次订货量和缺货量也可认为是关于促销因子的函数，进而认为收益函数是关于促销因子的函数。其中，促销因子为决策变量，而每次订货量和缺货量为中间变量。由此可知，优化的目标函数就是最大化收益函数Z[q（ρ），s（ρ），ρ]。其中，

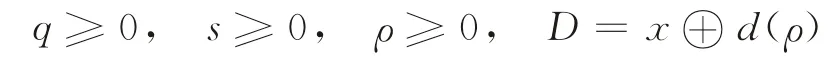
且满足式（2）、（3）。

2 模型求解

定理1对于任意ρ∈R+，存在唯一的q*和s*，收益函数Z达到最大值。此时，

其中，q≥0，s≥0，D=x⊕d（ρ），ρ≥0且满足式（2）、（3）。

证明显然，收益函数Z是关于促销因子的函数，在定义域内且为连续可积可微函数。根据定理条件，不妨假设：

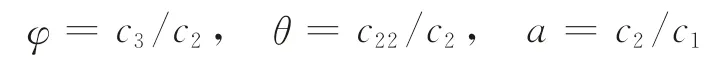
且ϕ＞0，θ＞0，a＞0。将上述假设代入式（1），得

对式（4）分别求偏导，得：

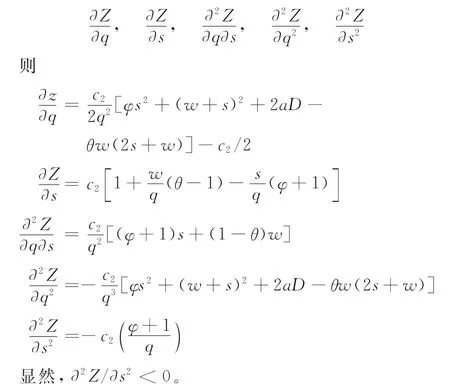
根据假设可知，c22＜c2，即0＜θ＜1，可得：

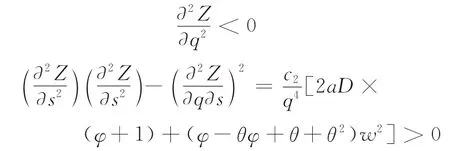
由上述分析可知，收益函数Z[q（ρ），s（ρ），ρ]是关于决策变量促销因子的函数，每次订货量和缺货量为中间变量，且存在最大值。可令∂Z/∂q=0，∂Z/∂s=0，整理得：

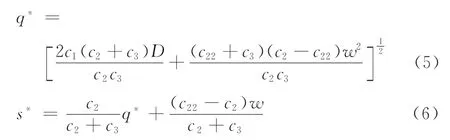
综上所述，对于任意ρ∈R+，存在唯一的q*和s*，使得收益函数Z达到最大值。 证毕

将q*和s*代入收益函数Z，整理可得

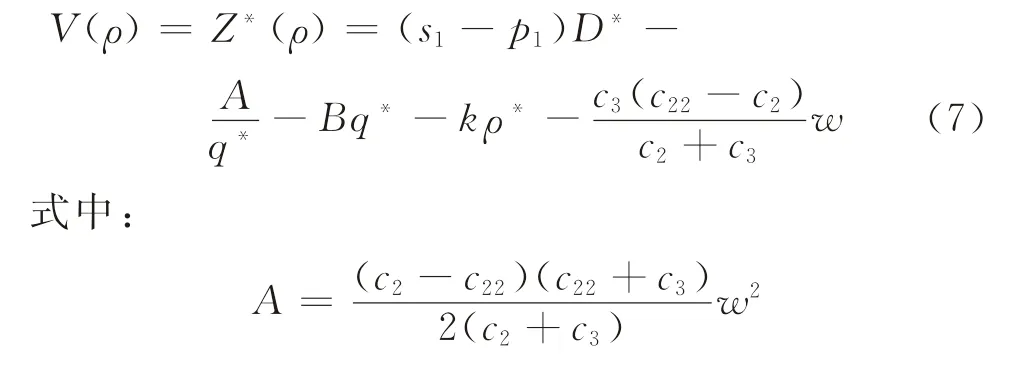
综上所述，求解V（ρ）最大化，存在ρ的最优解ρ∈R+，只需当时，求解出ρ*，并保证。通过观察V（ρ）可知，当ρ→∞时，V（ρ）→-∞。这表明，ρ存在上限解，使得V（ρ）＞0。不妨假设V（ρ）=0时，ρ的上限解为ρ**。

3 对比研究

考虑到文献[24]中主要研究了促销策略角度下的单库存系统的收益问题，为此，本节将通过与文献[24]中的数学对比分析，列出两种不同类型的数学模型，并尽量采用与文献[24]中相同的数值进行验算，研究促销因子影响程度和参数灵敏度，期望从与文献[24]的对比研究中得到有意义的研究结论。

3.1 数学对比分析

通过对比文献[24]，本文的收益函数为

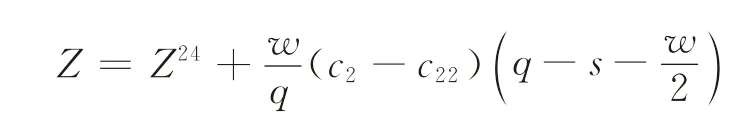
由假设可知，当w=0，或c22=c2时，即当OW 库存容量为0，或者单位OW 库存成本和单位RW 库存成本相等时，两层库存模型将转变为单库存模型。因此，本文的模型拓展了文献[24]中的模型。

一般的，Z≥Z24，即相同成本结构条件下，双层库存收益值不小于单层库存的收益值。这主要的原因是在保持正常经营的店面内开发了成本较小的店面仓库。增加的收益主要取决于OW 单位库存成本和RW 单位库存成本之间的差值，以及OW 的库存容量w。由函数分析可知，w在定义域[0，q-s]内与收益值之间呈正相关的趋势。因此，店面仓库库存不影响正常经营以及充分利用店面仓库容量必须同时兼顾，缺一不可。

3.2 数学模型

市场需求D与促销因子ρ之间存在两种对应的关系[24]，所需优化的目标函数分为模型I和模型II两种模型，即

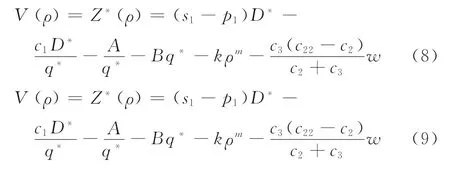
式中，D*=x+τρ/（1+ρ），且满足式（2）、（3）以及式（5）、（6）。

3.3 数值验算

针对模型I和模型II，为了便于对比研究，不妨参照文献[24]取值：x=70，τ=20，c1=28，c2=20，c22=10，c3=100，m=3，s1=20，p1=12，k=18，w=10，则：

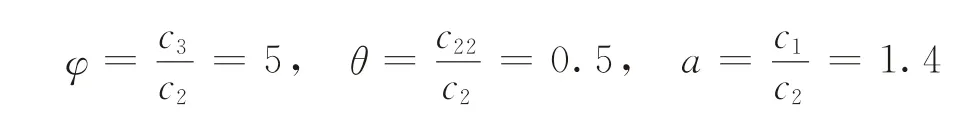
运算结果如表1、2所示。

表1 模型I和模型II的优化结果

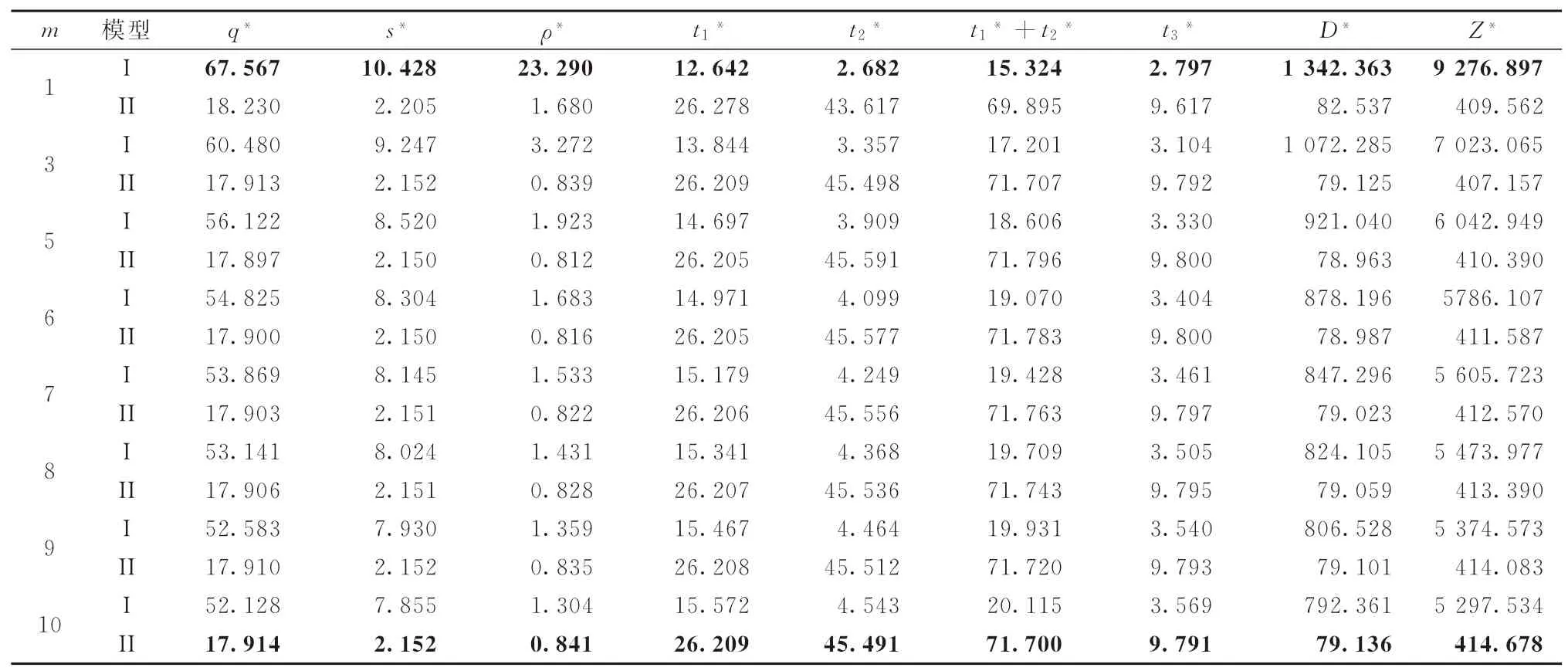
表2 不同m 值的模型I和模型II的优化结果

由表1、2以及对照文献[24]中的表1、2可知，由于店面仓库的存在，收益值均比相应无店面仓库的情况增加。与文献[24]中不同的是，库存存储时间是随着m而发生变化的，尽管变化的范围并不大。

通过运算可知，模型I、II的收益值和m值的相关性呈现不尽相同的趋势。m值是根据历史数据得到的经验估计值，一般而言，m值是固定的参数。表2给出了各种m值不同情况下的收益最优的结果。

3.4 促销因子ρ值的影响分析

根据假设，促销因子的变化将影响市场需求，从而进一步影响收益值。模型I、II的促销因子取值范围分别为（0.25，7.92），（0，2.935），收益值的变化情况如图2、3所示。由图2、3可知，模型I、II的促销因子ρ分别达到3.272和0.893时，收益值最大，分别为7 023.065和407.157。结合图形和运算结果可知，上述两种模型分别表示两类典型产品类型：模型I不做促销时，市场需求为0，收益值为负数，即-40.27；模型II不做促销时，市场需求不为0，收益值为正数，即359.412 4。

图2 模型I促销因子和每年收益函数图

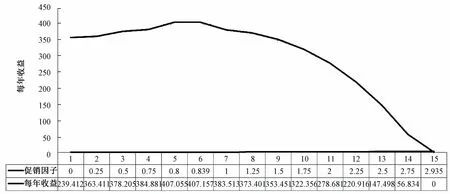
图3 模型II促销因子和每年收益的函数图

这与现实情况比较相符，为确保收益值达到最优，促销力度（促销因子）因视产品成本结构等实际情况而确定，不宜过大或过小。对比文献[24]中的图2、3，本文的图2、3相对比较完整地显示出促销因子和收益函数之间的关系。

3.4 灵敏度分析

对模型I的参数c1、c21、c22、c3、x、τ、s1、p1和k进行灵敏度分析，各参数独立采取从-50%～50%数值变化，从而观察收益值的变化情况；对模型II的参数灵敏度分析分别采用w=0和w=10两种情况进行比对，各参数独立采取从-50%～50%数值变化，从而观察收益值的变化情况。运算结果如表4～6所示。

由表4可以看出，模型I中的参数s1和p1为高灵敏度参数，x和τ为中灵敏度参数，c1、c21、k、c22和c3为低灵敏度参数。当销售价格s1增至原来的50%时，模型I的收益达到最大值18 070.070。

由表5可以看出，模型II中的参数s1和p1为高灵敏度参数，x和c1为中灵敏度参数，c21、c22、c3、τ、和k为低灵敏度参数。当销售价格s1增至原来的50%时，模型II的收益达到最大值1 207.525。

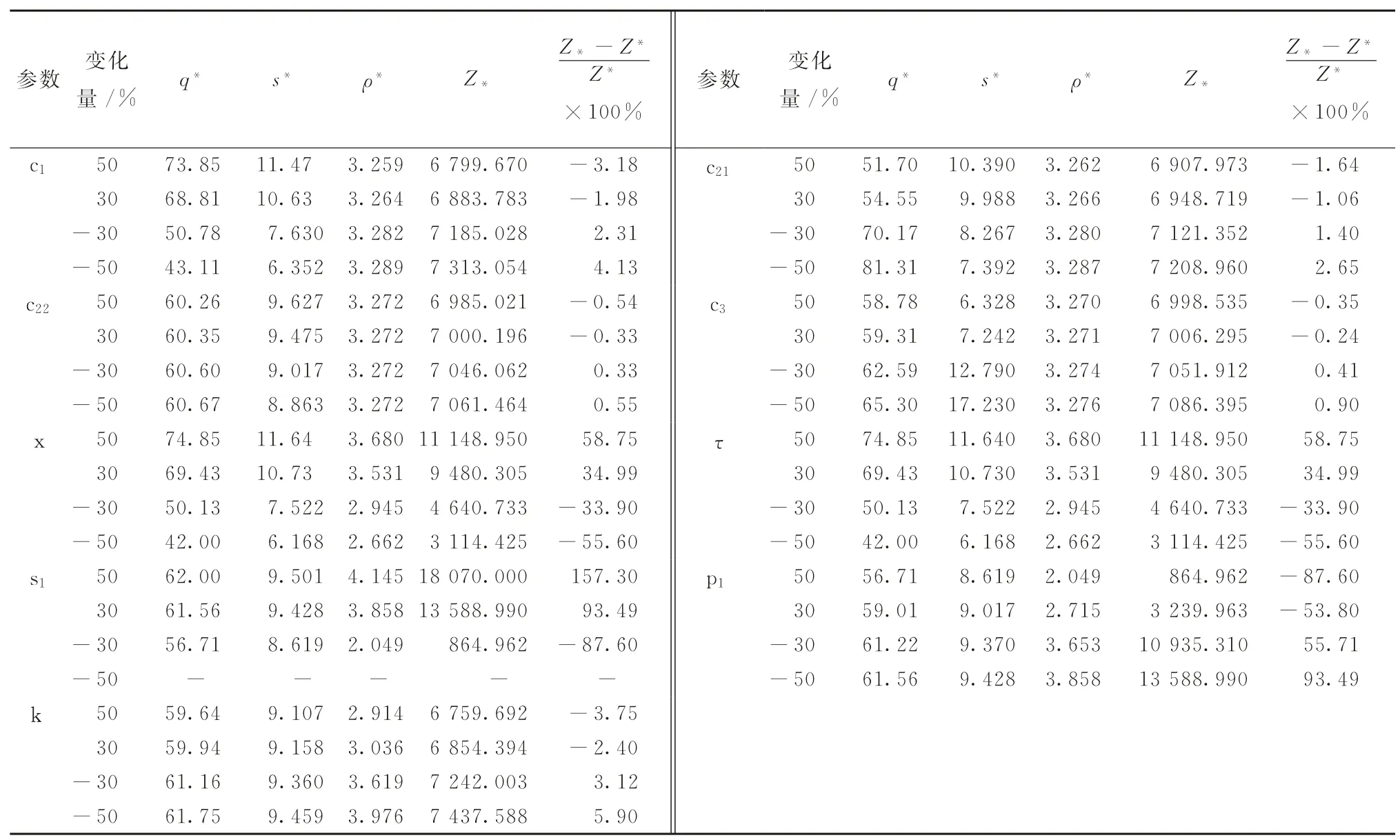
表4 模型I参数灵敏度分析

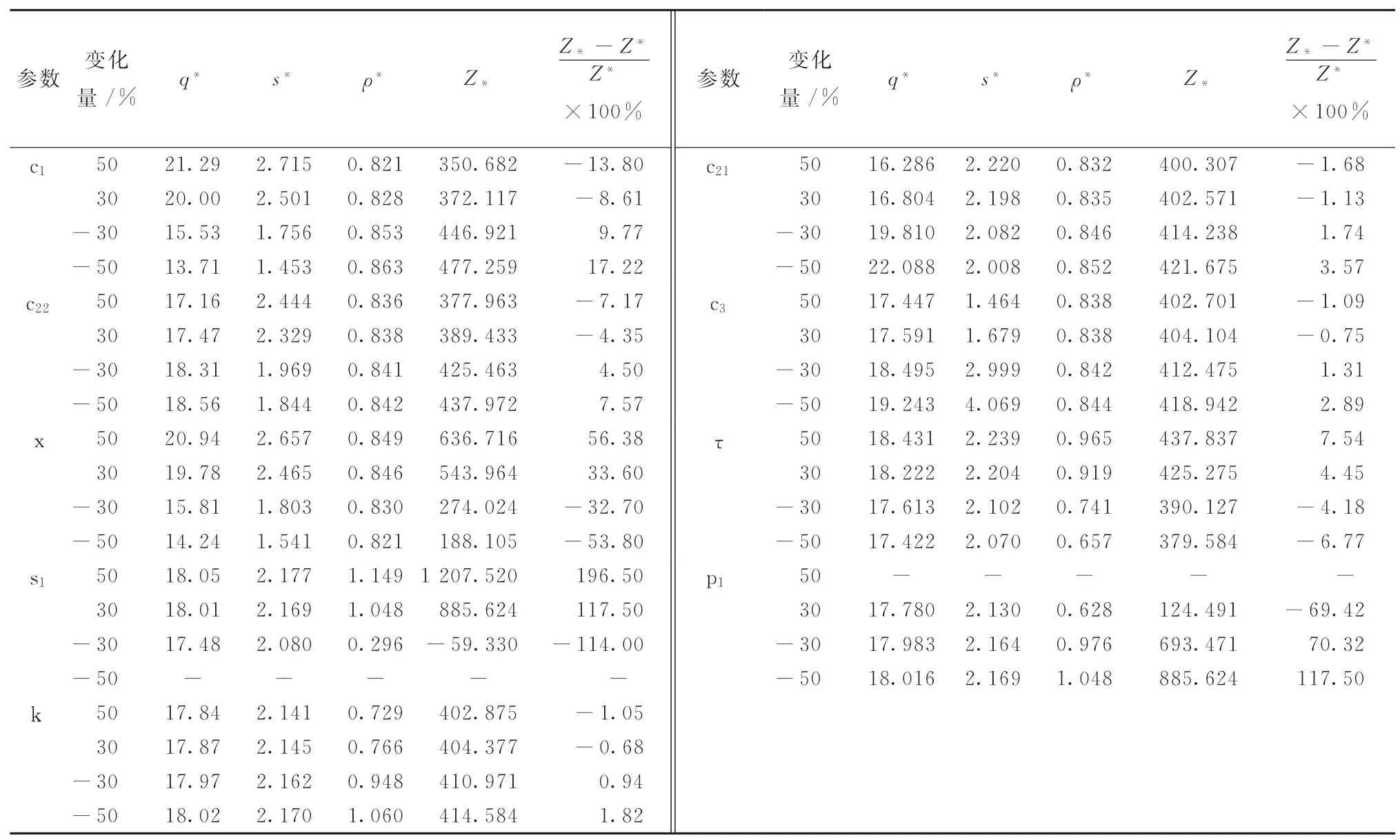
表5 模型II参数灵敏度分析(w=10)

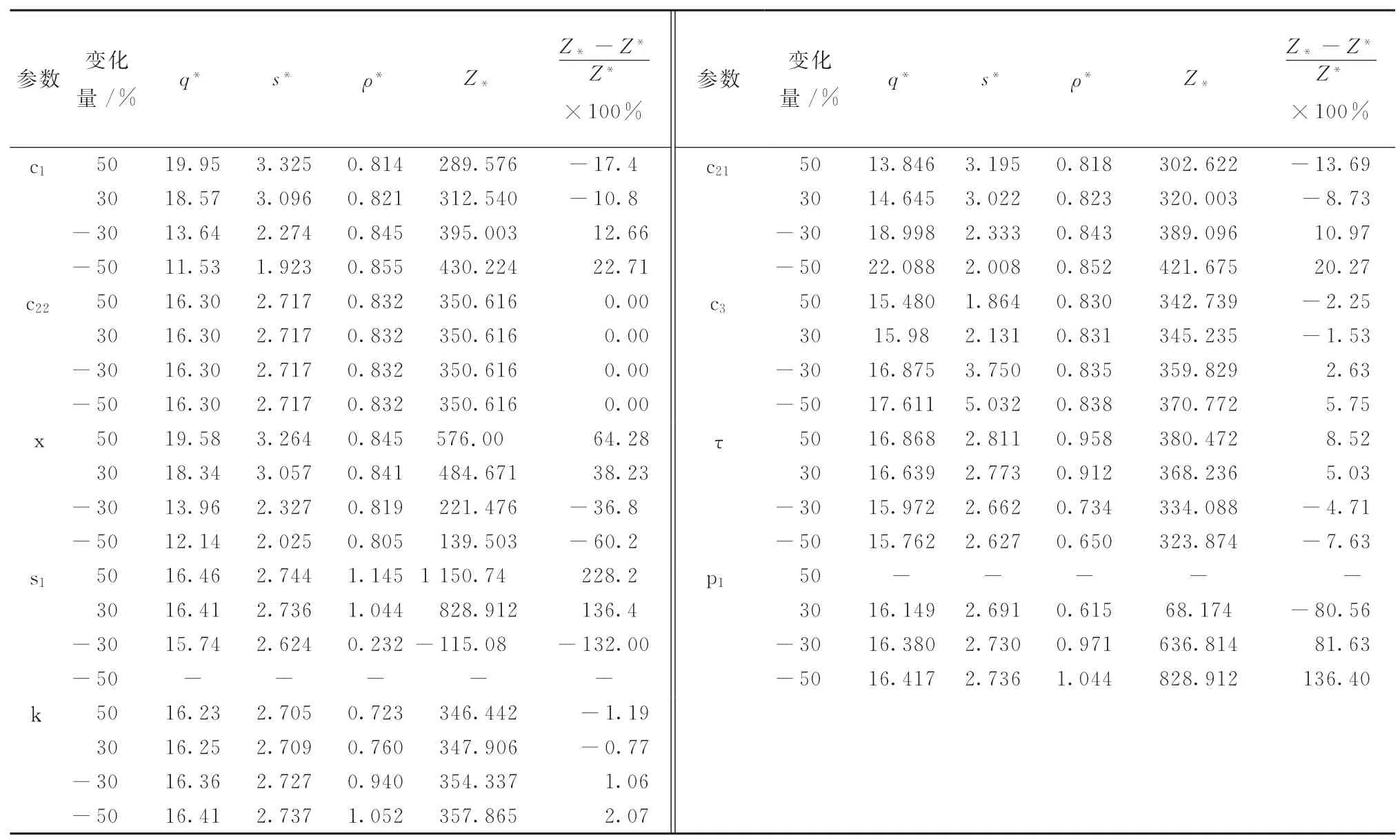
表6 模型II参数灵敏度分析(w=0)

对比文献[24]中的表7（以下简称表7）和本文的表4可以看出，同等条件下，表4的各参数灵敏度均小于表7，而此时的收益值却均大于表7的收益值。类似地，同等条件下，表5中的各参数敏感度均小于表6，而此时的收益值却均大于表6 的收益值。因此，可以认为店面仓库在一定程度上降低了收益值的波动率而提高了同等条件下的收益值。

4 结论

本文从实施促销策略角度构建了允许缺货的两层仓库库存模型，假设模型的收益值是关于促销因子的函数，根据产品类型分为两种不同形式的模型，并深入研究了店面仓库库存容量以及促销因子等因素对两层库存系统收益的影响。通过数值分析，获得了如下主要结论：

（1）对于不同产品或相同产品处于不同的竞争环境下，促销策略的实施效果不尽相同。实施促销策略之前，明晰本产品的收益值函数的组成形式，充分重视收集产品的历史数据，确定合适的促销力度等，以达到收益值最大。

（2）对于单层库存而言，两层仓库中的店面仓库容量改变了单层库存的成本结构，并起到了减少收益值的波动性和提高收益值的双重作用。进而，在确保店面库存容量不影响店面正常经营的前提下，充分利用店面仓库容量，综合考虑历史数据等因素，可通过事先规划店面仓库容量的方法，提高收益值的水平；或在店面仓库容量固定的情况下，通过调整促销力度等因素，优化收益值。

（3）对于两类不同形式的产品，提高销售价格和降低购买成本均可迅速增加收益值。若上述两种方式均不可行时，符合模型I的产品可通过增加参数x和τ而达到收益值最优，即通过生产真正符合消费者需求的产品以及根据产品类型和消费者特点采取适宜的促销方式增加促销效果等方法；符合模型II的产品可增加参数x、减少参数c1，使得收益值最优，即除了生产真正符合消费者需求的产品外，还可通过努力降低每次订货成本等方法。

结合模拟算例的比较和灵敏度分析易知，本文所建构的模型进一步拓展了文献[24]中经典模型的结论及其适用范围，较为全面地刻画出两层库存的商业运作情况。同时，通过定量理论模型分析系统地阐明了促销因子等因素与收益值之间的关系，进而给出具有针对性的、可行性较强的对策建议。因此，本文所构建的模型能够尽可能地刻画实际中的库存问题特征，因而具有较好的应用型和适用性。

事实上，在本文研究的基础上，考虑到竞争环境下促销因子等因素不应保持不变，如若将促销因子等参数进行模糊化处理，可进一步提高模型的适用性。另外，本文未考虑零售商最优订货量和允许缺货量的决策次序，也未考虑两类模型所代表的具体产品类型及其特征。这些问题将在未来的研究工作中继续深入探讨和研究。