双寡头竞争环境下的补贴对象选择问题

徐磊 ，董明，陈靖

（1.上海交通大学 安泰经济与管理学院，上海 200030；2.上海外国语大学 国际工商管理学院，上海 200083）

补贴作为一种利用资金帮助企业和消费者以促进社会福利的手段，一直以来都被国内外政府或非营利机构广泛地采用。其应用范围也十分广泛，从传统的农业（如粮食[1]、棉花[2]）、日常食品（如燕麦牛奶[3]等）和生活必需品（如药物[4-6]、眼镜[7]等），到现代的绿色科技（如太阳能[8]、新能源汽车[9]）和优质生活（如健康饮食[10-11]）等方面。

实践证明，具体的对企业或个人的补贴方式的制定和执行，对补贴策略的影响十分显著。同时，由于社会福利等传统指标的难以刻画性，加之在大部分情境下，促进市场整体消费量都是比较合理的目标和方向，特别是在新兴产业、或求过于供的疫苗案例[12]等情况下。因此，总销售量成为另一个重要的评价指标。特别是市场总销售量与补贴总成本之间的平衡这一研究问题，因其广泛的应用背景而获得了较多的关注，如太阳能技术[13]、新能源汽车[9]等需要一定数量的消费者采用才能形成规模效应，使得整体获益；疟疾药物或疫苗应当达到一定的普及程度，才能对整个地区的疾病控制有比较好的效果。

然而，长期以来，相关的研究主要集中在经济政策领域，讨论税收等具体方式的实施与效果[14-19]。Fullerton等[16]较为详尽地呈现了该领域中非完全竞争模型下较为经典的一些研究成果，他们假设面对的是同质的企业，研究讨论税收对市场中参与竞争的企业数量的影响，进而考察税收作为一种补贴方式对消费者的影响。Leahy等[20]在线性需求的假设下，考虑在国际贸易竞争中，政府应当选择如何利用补贴工具调控本国企业的产量，以使得己方社会福利最大化。但是在模型假设中，政府能够直接选择本国企业产量；同时，进一步假设已知政府资金的机会成本，故并未体现出补贴如何具体产生作用的过程。

运营范畴内相关的研究在近年来逐渐增加。以最大化销售量为目标，Taylor 等[12]及Berenguer等[21]均直接选择了作为补贴对象的某一企业或非营利组织展开研究，前者以多阶段模型讨论采购补贴和销售补贴对企业的影响，后者则重点比较该两种方式分别实施在企业与非营利组织上的效果。目标同样是促进社会整体消费量，Levi等[22]集中讨论了在不完全竞争下，补贴对象为行业中所有企业且每单位补贴均相同这一补贴方式的效果。尽管在假设中企业是存在差异的，但是文中并未对企业之间的比较和选择进行讨论。Lobel等[13]以最小化补贴总额为目标，讨论了政府应当如何制定补贴策略以鼓励选择太阳能的消费者达到一定数量。此研究中，补贴直接作为安装补助费用，直接发放至消费者。

本文的研究方向与上述文献一致，目的为讨论补贴政策制定者如何能够在整个市场的销售量达到期望增量的基础上尽可能降低补贴总成本。理论贡献在于采用了文献中普遍使用的线性需求为假设，从理论上分析面对两家竞争型企业时，如何选择补贴对象（包括企业和消费者）并制定相对应的每单位补贴额度。同时，由于目标和假设的一般性，理论研究结果的适用范围将较为广泛，不仅能够使政府及社会建设参与度和影响力逐渐增加的非政府机构对补贴对象的选择有更深入的认识，也能为这些补贴政策制定者在实践中如何制定具体的补贴方式以平衡补贴费用与市场销售量提供一定的参考。

1 模型与假设

考虑两家寡头竞争企业A和B，分别生产销售有差异的同类型产品A和产品B（为表述方便，A和B同时表示企业和产品，在无歧义的情况下不作区分）。根据经济学原理，假设产品需求函数为

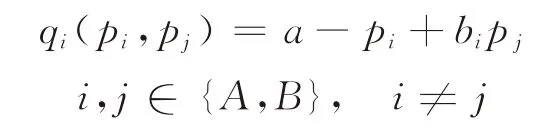
其中：a为市场容量；b∈[0，1]为产品B的定价p B对产品A的需求的影响，反映了两者之间的替代性。当bi=0 时，意味着两者不可替代；当bi=1时，则为完全替代品。

出资方考虑3种单一补贴方式，分别对应不同的补贴对象，即将补贴发放给企业A，或企业B，或直接发放给消费者。假设企业i所获得的每单位产品补贴额度为w i≥0，消费者所获得每单位产品补贴额度为w C≥0。其优化问题在于，如何制定补贴方式，以最少的花费达到既定的目标销售额增量ΔQ。因此，整个博弈事件顺序为：

（1）出资方宣布补贴方式（w A，w B，w C），其中，w Aw B=w Bw C=w Cw A=0；

（2）企业根据市场需求、补贴方式和成本ci，以最优化利润为目标，各自对产品进行定价pi；

（3）消费者根据产品价格和补贴方式进行选择，产品i的销量为

（4）出资方根据最初制定的补贴方式，发放对应的补贴。

下文将采用倒序求解法，首先分析给定补贴方式（w A，w B，w C），企业的最优决策和相应的消费者选择；然后据此分析比较不同的补贴方式，进而得到出资方的最优决策。

1.1 企业最优决策：无补贴情况

定理1企业i的最优定价为

对应的销量为

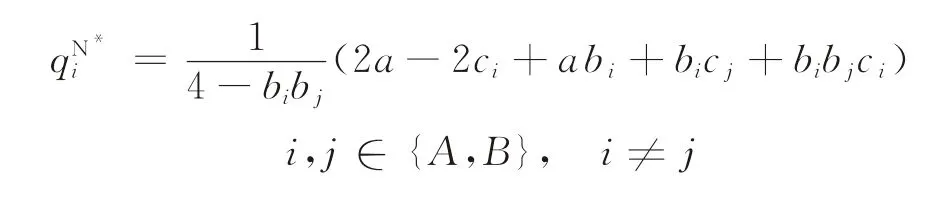
证明企业i的收益为

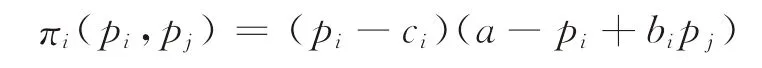
对p i求一阶导数，可得

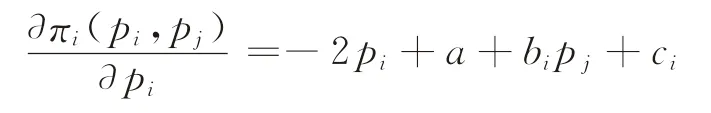
根据一阶导最优条件，令其等于0求解可得。

证毕

根据定理1，可以进一步比较两种产品的市场占有情况。

推论1产品A的销量高于产品B的销量（即当且仅当b A-b B＞α（c A-c B）满足时，其中，α=（2-ba b B+b B）/（a+c B）。

由推论1可知，产品A拥有较高市场占有率主要有如下3种情况：

（1）产品A具有较好的替代性，同时还拥有较低的单位成本，即b A＞b B，并且c A＜c B。这种情况下，产品A在两方面均具有竞争优势，故而占据了较大的市场份额。

（2）产品A具有较好的替代性，但是单位成本较高，即b A＞b B，并且c A＞c B。此时，产品A若仍能占据较大的市场份额，其在替代性上的优势必须超过成本上的劣势，即（b A-b B）/（c A-c B）＞α。

（3）产品A具有较差的替代性，但拥有低成本的优势，即b A＜b B，并且c A＜c B。该情况下，当产品A较差的替代性的劣势能够被低成本的优势超过，即（c B-c A）/（b B-b A）＞1/α时，才能够拥有较大的市场占有率。

总结而言，企业双方在竞争时，关键点在于产品替代性（消费者偏好）和成本两方面。当该企业产品在两方面都能获得竞争优势，或在一方面的竞争优势足够大时，将能够占据市场有利地位。

1.2 企业最优决策：有补贴情况

当企业i所获得的每单位产品补贴额度为w i，消费者所获得每单位产品补贴额度为w C时，产品i的需求函数为

定理2给定每单位产品补贴额度（w A，w B，w C），企业i的最优定价为

对应的销量为

证明企业i的利润为

对其求p i的一阶导数，可得

令∂πi（p i，p j，w A，w B，w C）/∂pi=0，求解可得

证毕

因此，有补贴情况下的最优价格和数量决策可以进一步表示为：

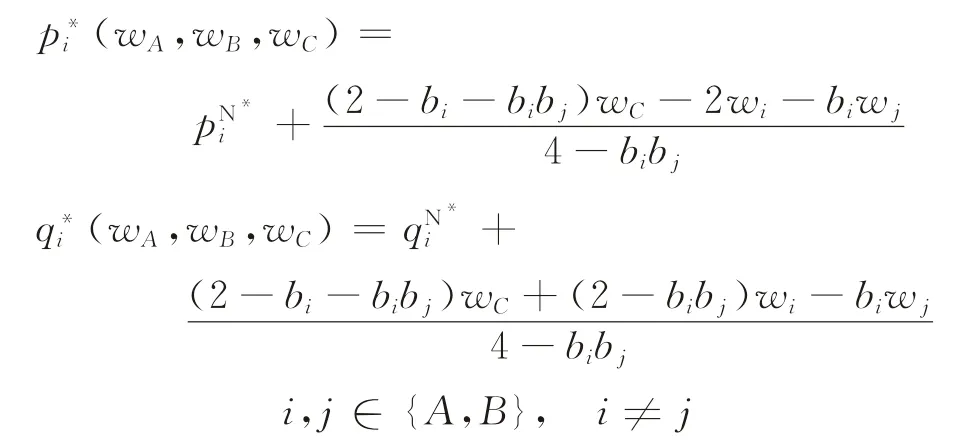
由此可知，补贴的发放总是能够使得对于消费者而言的实际价格降低，整个市场的销售量增加。若补贴对象为某一产品，则该产品的销量将增加，另一产品的销量将降低；若补贴对象为消费者，则两种产品的销量均会增加。相同单位补贴额所带来的具体补贴效果，即对销售量的影响则是由两种产品之间的相互替代性所决定的。

2 补贴对象的分析与选择

本章将对出资方的决策进行分析，考虑如何制定具体的补贴方案，使得达到给定目标增量时所花费的补贴总额最少。

令Q（w A，w B，w C）表示给定补贴方式（w A，w B，w C）下的市场总销售量，QN表示无补贴时的市场总销售量，于是有

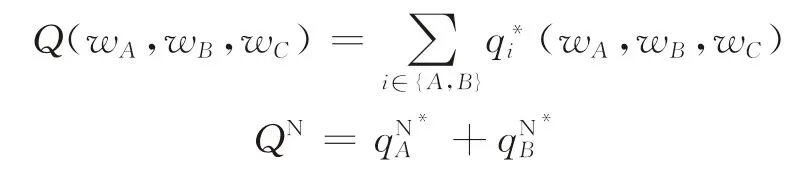
同时有约束条件：

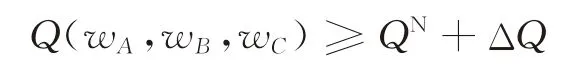
由于销售量均随单位补贴额度单调增加，而出资方的目标在于最小化补贴总额，故最优决策必然会使上述条件取等，否则总是可以在不改变不等式符号的条件下降低每单位补贴额度进而减少补贴总额。

因此，如果选择补贴企业A，则必然有

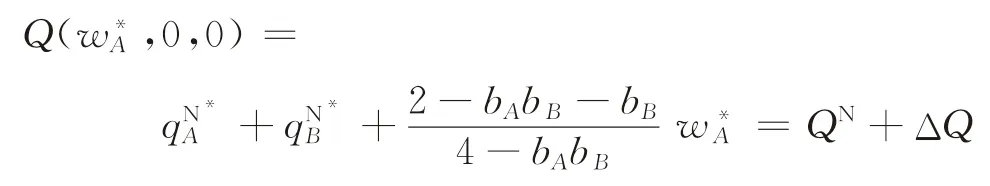
求解可得最优的单位补贴额度：

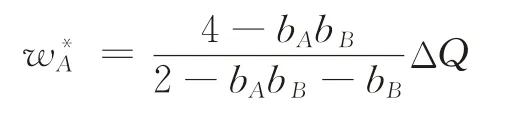
所需要花费的补贴总额为

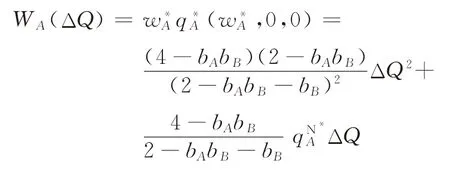
同理可得选择补贴企业B或消费者时的最优补贴决策。

定理3给定目标增量ΔQ：

（1）若选择补贴企业i，最优单位补贴额度和补贴总额分别为：

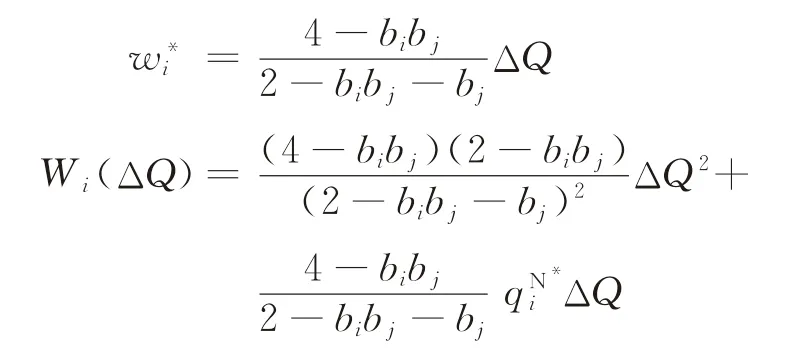
其中，i，j∈｛A，B｝，i≠j。

（2）若选择补贴消费者，最优单位补贴额度和补贴总额分别为：

通过定理3的结论可知，在任何一种补贴方式下，最优单位补贴额度和补贴总额均随目标增量的单调增加，且补贴总额是关于目标增量的凸函数。3种补贴方式的区别在于，由于产品替代性和成本的差异，故造成的增长率不同。

2.1 补贴对象选择：企业A 或企业B

首先考虑如果要选择一家企业进行补贴，应当如何进行分析与比较。选择企业A和企业B的补贴总额差异为

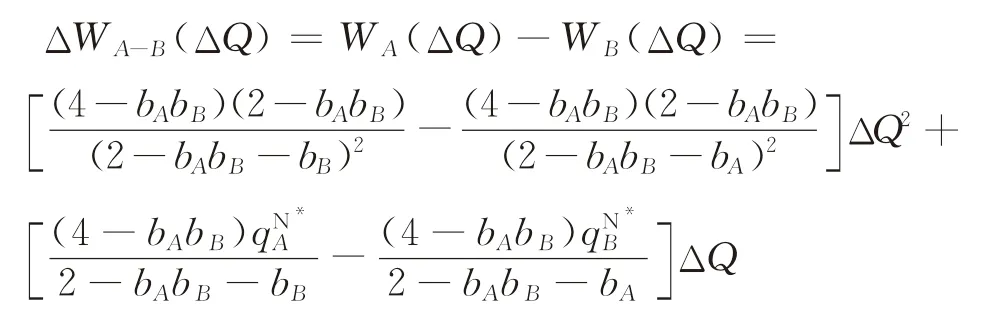
定理4假设b A≥bB：

（1）若

则当ΔQ∈[0，+∞）时，ΔW A-B（ΔQ）≤0。

（2）若

则存在

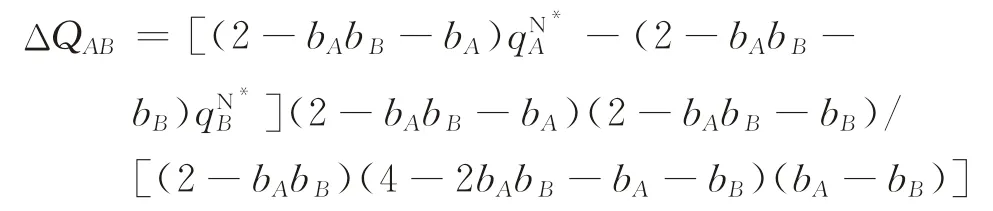
当ΔQ∈[0，ΔQAB]时，ΔW A-B（ΔQ）≥0；当ΔQ∈（ΔQAB，+∞）时，ΔW A-B（ΔQ）＜0。

证明由于

b A和b B的差异决定了当ΔQ足够大时，两者补贴总额的差异。即若b B-b A≤（＞）0，则当ΔQ足够大时，有ΔW A-B（ΔQ）≤（＞）0。因为企业A、B在本文中处于对等的地位，所以，可以不失一般性地集中讨论b A≥b B的情况。

令ΔW A-B（ΔQ）=0，可得

由定理4可知，若b A≥b B，随着目标增量ΔQ的提高，最终选择产品A的补贴总额会低于产品B。这表明，当目标增量较大时，应该更加关注产品的替代性，即消费者对产品的偏好在长远上决定了补贴应该选择的对象企业，故在此情况下，应该选择产品替代性较好的企业。

而当目标增量相对较小时，则存在如下两种情况：

（1）应当选择产品A当其替代性较好，即b A≥b B，且市场占有率不是特别高之时，即

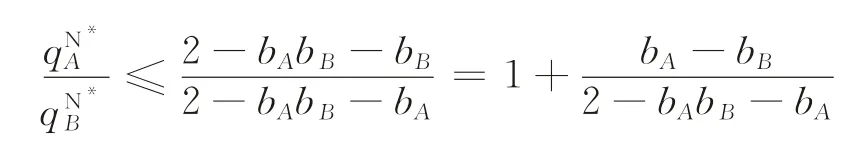
（2）应当选择产品B当其替代性较差，即b B≤b A，同时市场占有率较低时，即

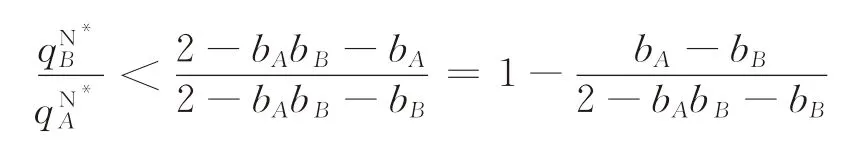
两种情况的共性是，被选择进行补贴的产品均拥有相对较低的市场占有率和相对较高的成长速率，所以，此时每单位补贴所带来的效果会相对较大。因此，当目标增量较小时，选择这种产品进行补贴会见效比较快。

2.2 补贴对象选择：企业或消费者

考虑将补贴直接发放给消费者，则此补贴方式所需的总额与补贴给企业i的总额的差异为

引理1对于i，j∈｛A，B｝，i≠j，有：

（1）若

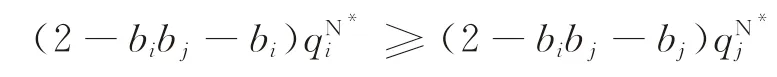
当ΔQ∈[0，+∞）时，ΔW C-i（ΔQ）≤0。

（2）若

则存在

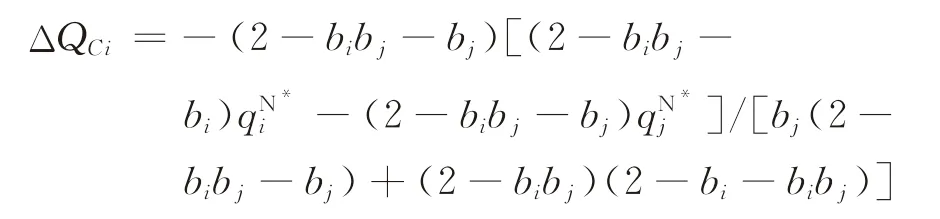
当ΔQ∈[0，ΔQCi]时，ΔW C-i（ΔQ）≥0；当ΔQ∈（ΔQCi，+∞）时，ΔW C-i（ΔQ）＜0。

证明由于

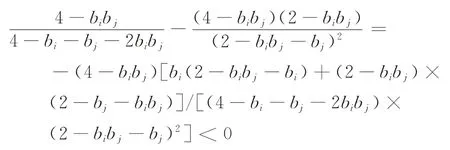
故当ΔQ足够大时，将有ΔW C-i（ΔQ）＜0。

令ΔW C-i（ΔQ）=0，可得

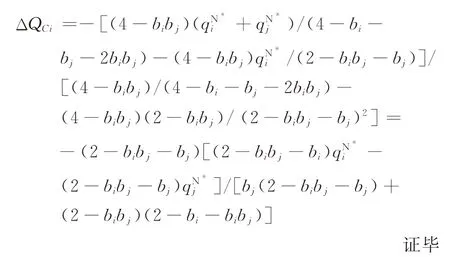
引理1表明，当目标增量较大时，应当直接补贴给消费者。值得注意的是，此时在企业或消费者的选择上，产品替代性不再像之前在企业间选择一样具有决定性影响。原因在于，从长远来看，对于消费者而言，相比较于产品的降价，最偏好的还是直接给予补贴。

而当目标增量较小时，则要根据具体情况进行选择，由于短期增长速率的不同，企业或消费者都有可能是最优补贴对象，故需要对3个门槛值企业A或企业B（ΔQAB）、消费者或企业A（ΔQCA）以及消费者或企业B（ΔQCB）进行进一步的比较分析。

首先比较ΔQAB与ΔQCA。两者的差异为

同理可得，ΔQAB与ΔQCA的差异为

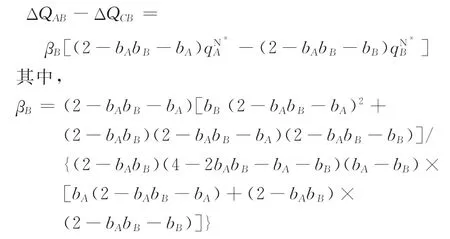
不失一般性，仅讨论b A≥b B的情况，可得此时最优决策如定理5所述。

定理5假设b A≥b B：

（1）若

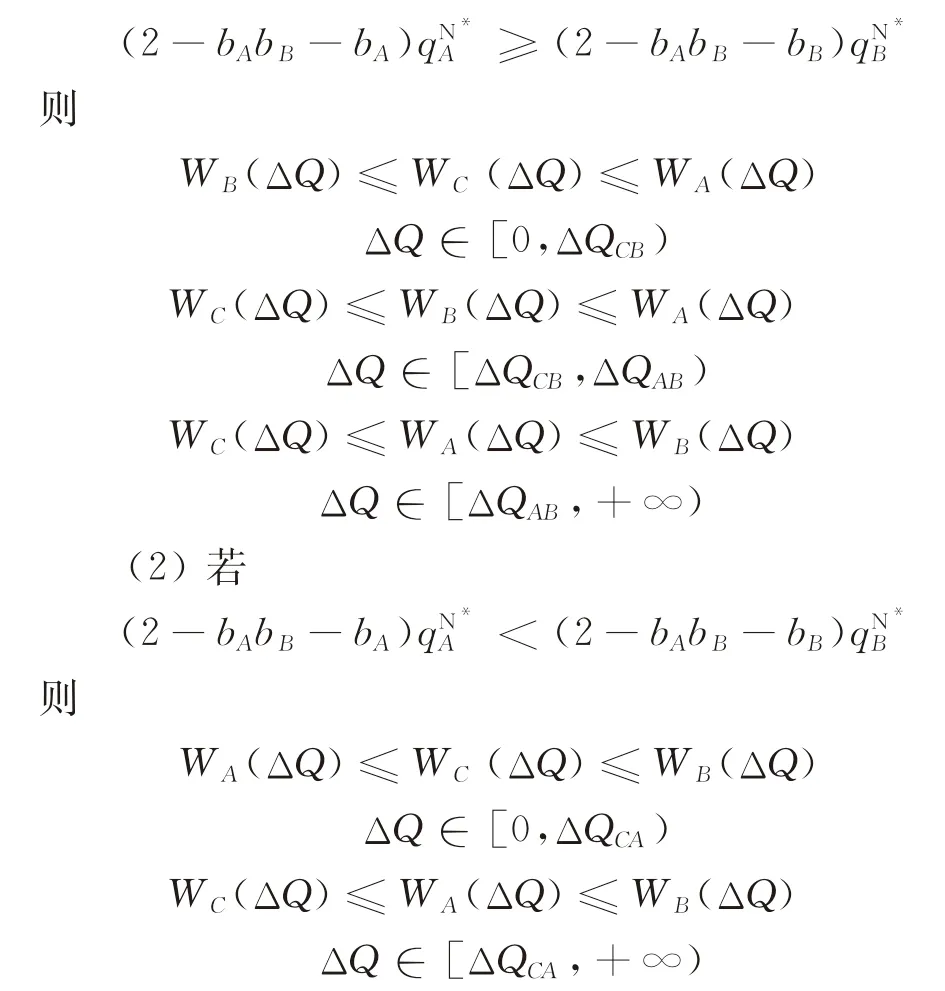
证明当b A≥b B时，可知，βA＞0，βB＞0。

（1）若

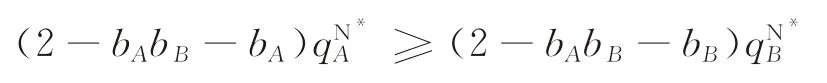
则有

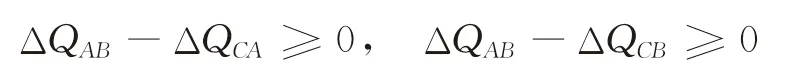
根据引理1可知，此时，ΔQCA≤0，ΔQCB≥0。同时，由定理4可知，ΔQAB≥0。于是可得ΔQCA≤0≤ΔQCB≤ΔQAB。

根据定理4和引理1的结论可知：

①当ΔQ∈[0，ΔQCB）时，有：

故W B（ΔQ）≤W C（ΔQ）≤W A（ΔQ）。

②当ΔQ∈[ΔQCB，ΔQAB）时，有：

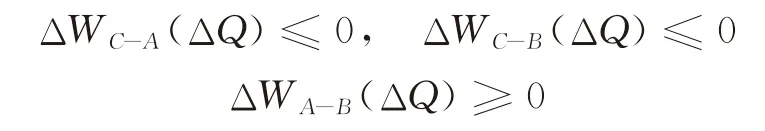
故W C（ΔQ）≤W B（ΔQ）≤W A（ΔQ）。

③当ΔQ∈[ΔQAB，+∞）时，有：

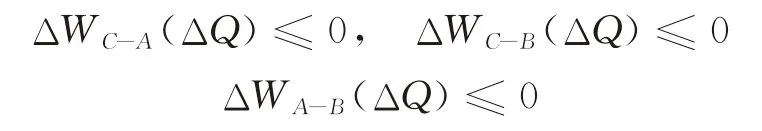
故W C（ΔQ）≤W A（ΔQ）≤W B（ΔQ）。

（2）若

则有

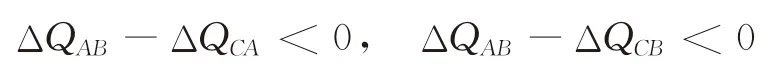
同时可知，ΔQAB＜0，ΔQCA＞0，ΔQCB＜0。因此，有ΔQAB＜ΔQCB＜0＜ΔQCA。

①当ΔQ∈[0，ΔQCA）时，有：

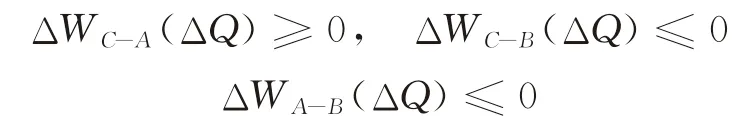
故W A（ΔQ）≤W C（ΔQ）≤W B（ΔQ）。

②当ΔQ∈[ΔQCA，+∞）时，有：

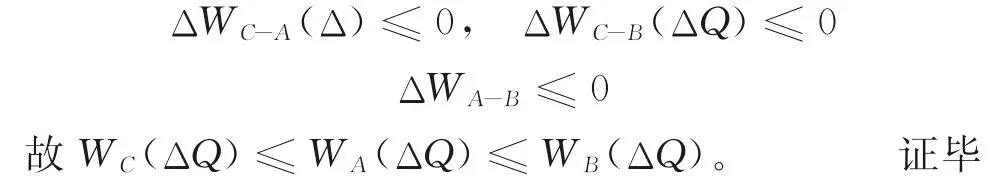
定理5表明，当目标增量较小时，应当选择补贴给企业。原因在于，由于产品的替代性和成本之间的差异，在最初时，每单位补贴给产品A或是B所带来的销售量增加的效果不同，故此时应根据具体情况，选择某一家企业进行补贴。当补贴不同企业所带来的边际增量相同时，如果只能选择某一家企业进行补贴且每单位补贴均可进行一次选择，则应当是在两者之间交替进行。因此，在此情况下，选择直接补贴消费者更为明智，因为本质上而言，相当于是同时补贴两家企业。

3 数值分析

本章将采用数值分析的方式，对不同环境参数条件下，对各种补贴方式进行分析和比较。

3.1 补贴对象的比较与选择

首先讨论最优补贴对象的选择问题。根据上文的结论，不失一般性，在假设b A≥b B的基础上进行进一步讨论。此时，又有两种情况，即c A≥c B和c A＜c B。

考虑第1种情况，即c A≥c B时。令a=100，b A=0.8，b B=0.56，c A=10，c B=6，在无补贴时，产品A、B的最优销售量分别为=75.81，=71.03。当目标销售额增量ΔQ从1增至11时，各补贴方式所需总额之差如图1所示。

图1 a=100，b A=0.8，bB=0.56，c A=10，c B=6 时，各补贴方式所需总额之差

为方便讨论，定义

在此算例中，Condition=-13.15＜0，对应于定理5中的第2部分的讨论。根据图1可知，面对同样的目标销售增量，选择单独补贴企业A所需要的补贴总额总是少于单独补贴企业B所需的补贴总额，且两者之间的差异随目标增量的增加而增加。同时，选择单独补贴企业B所需的补贴总额总是多于选择直接补贴消费者所需的补贴总额，两者之间的差异也随目标增量的增加而增加。但对于单独补贴企业A和直接补贴消费者之间，则需要进一步考虑目标销售增量的大小。当目标增量较小时，即图1 中小于8的部分，选择单独补贴企业A所需的补贴总额较少；而当目标增量大于某一值（图1 的算例中为8）之后，则选择直接补贴消费者所需的补贴总额将较少，两者之间的差异随目标增量的增加，先增加然后降低为0，之后又逐渐增加。因此，在补贴方式的选择上，为在补贴增量低于某一门槛值时，选择单独补贴企业A，高于该门槛值之后，选择直接补贴消费者，与定理5的结论一致。

图2考虑第2种情况，即c A＜c B时。其中参数取值分别为a=100，b A=0.8，b B=0.16，c A=10，c B=30，此情况下若无补贴，产品A、B的最优销售量分别为=41.69，Condition=7.6＞0，对应于定理5中的第1部分的讨论。图2呈现了当目标增量从1增至7.5时，各补贴方式所需补贴总额之差。此情况下，面对相同的目标销售增量，单独补贴企业A所需的补贴总额总是高于直接补贴消费者所需的总额，且两者之间的差异随着目标增量递增。同时，单独补贴企业A所需的补贴总额在目标增量较小时，也高于单独补贴企业B所需的补贴总额，但当目标增量较大时，此算例中为大于4.5的部分，则前者所需的补贴总额少于后者，两者之前的差异先增大后减少为0，此时较优的选择发生改变，后又逐渐增大。而单独补贴企业B和直接补贴消费者相比，前者只有在目标增量较小时所需的补贴总额较少，即算例中小于2的部分，前者优势逐渐减少为零后，后者的优势逐渐增大。由上述分析可知，在补贴方式的比较上，存在两个门槛值，此算例中为补贴企业A和B之间的8，及补贴企业B和消费者之间的2；在补贴方式的选择上，只需考虑较小的门槛值，低于该值时，选择补贴企业B，高于该值后则选择直接补贴消费者，亦与定理5的讨论一致。

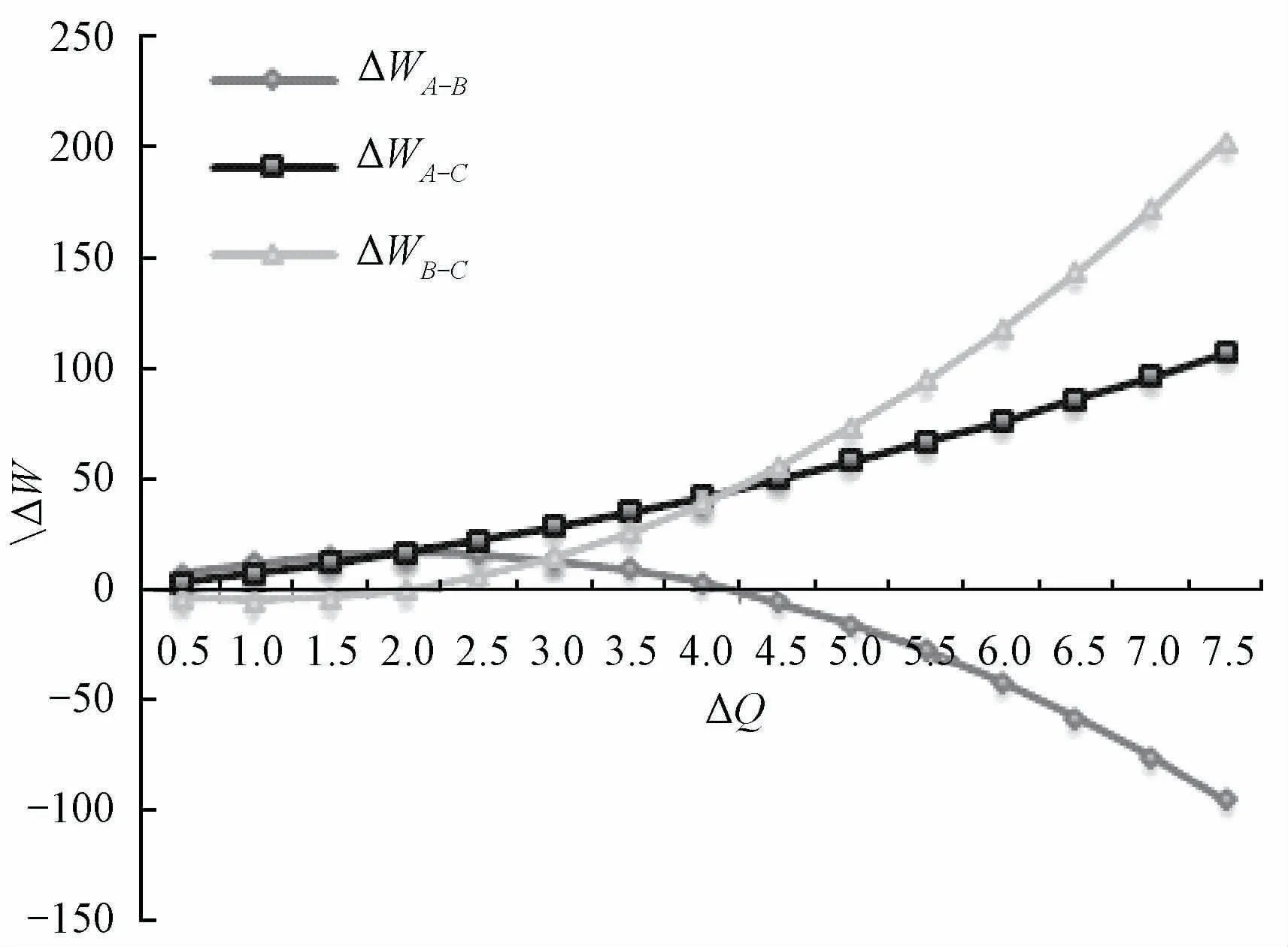
图2 a=100，b A=0.8，c A=10，bB=0.16，c B=30时，各补贴方式所需总额之差

同时比较图1、2两个算例可以发现，尽管具体的优劣有所区别，但是两者之间整体的趋势是非常相似的。在目标增量超过一定要求后，三者相比，都是直接补贴消费者最优，补贴企业A次优。而在目标增量较小时，都应当选择某个企业进行补贴；同时，值得注意的是，选择补贴企业的优势都呈现了先增加后减少的趋势。

3.2 敏感性分析

由上文的分析可知，在补贴对象的比较和选择上，存在一个门槛策略，接着将对各个参数进行敏感性分析，进一步检验和理解门槛策略在不同参数环境下的变化，以供决策者在选择和制定具体补贴方式参考。

首先讨论关于参数a的敏感性分析，依旧在b A≥b B的基础假设下，考虑c A≥c B和c A＜c B两种情况。图3展示了两个典型算例的结果。图3（a）为c A≥c B的一个算例，参数分别为：b A=0.8，b B=0.4，c A=10，c B=20。运算结果显示，当a从56 增加至65时，Condition、ΔQAB和ΔQCB均呈递减趋势，且均由一个正值减至一个负数；与此同时，ΔQCA由一负值递增至一正数。如定理5 讨论结果一致，四者的正负变更点一致。图3（b）为c A＜c B的一个算例，参数分别为：b A=0.6，b B=0.048，c A=10，c B=9。运算结果显示，尽管具体数值结果不同，但是整体趋势与左侧算例是相同的。

综合两个算例的结果可知，作为可选的补贴对象，企业或消费者并没有哪一个是在所有参数环境下都占优势的，且如定理5的讨论结果所述，目标增量较小时，补贴企业为较优的选择，而目标增量较大时，应当选择直接补贴消费者。同时，可见，当参数a增大时，由定理5中第1部分讨论结果逐渐转变为第2部分讨论的结果，即目标增量较小时，单独补贴企业B的方式从占有优势，到逐渐失去优势至最终被单独补贴企业A的方式所替代。并且，在最优选择不变的情况下，若最优选择为先补贴企业A，后直接补贴消费者，则该目标增量的门槛值随着a的增加而增加；而若是最优策略为先补贴企业B，门槛值则是随着a的增加而递减的。

图3 参数a的敏感性分析

为了对参数b和c进行敏感性分析的讨论，定义

令a=30，b A=0.8，c A=10，图4～7呈现了当θb从0.01 递增至0.91、θc从0.7 递增至1.5 时，Condition、ΔQAB、ΔQCA以及ΔQCB的运算结果。与图1的结果相同，不存在唯一的补贴方式在所有参数环境下最优。

由图4结果可知，给定b A和c A时，Condition随着θb的增大先减小后增大，且呈负值的区间随着θc的增大而减小。同时，Condition的值随着θc的增大由负值单调递增至正值，并且，由负变为正的这一边界值随着θb的增加先增大后减小。这意味着在b B相对中等、c B相对较小时，补贴产品A是相对比较好的选择，这也符合前文的分析，因为此刻产品A的市场占有率不是特别高，每单位补贴所能带来的销售增量将更为有效；而当b B与b A的差异较大，或c B较大时，补贴产品B成为了更好的选择。

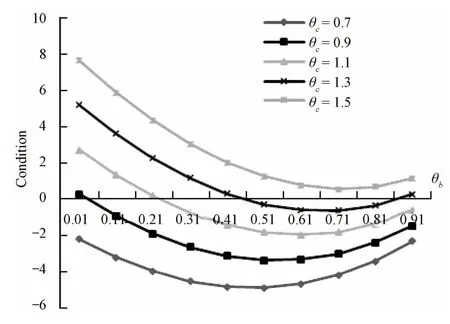
图4 参数b和c 关于Condition的敏感性分析

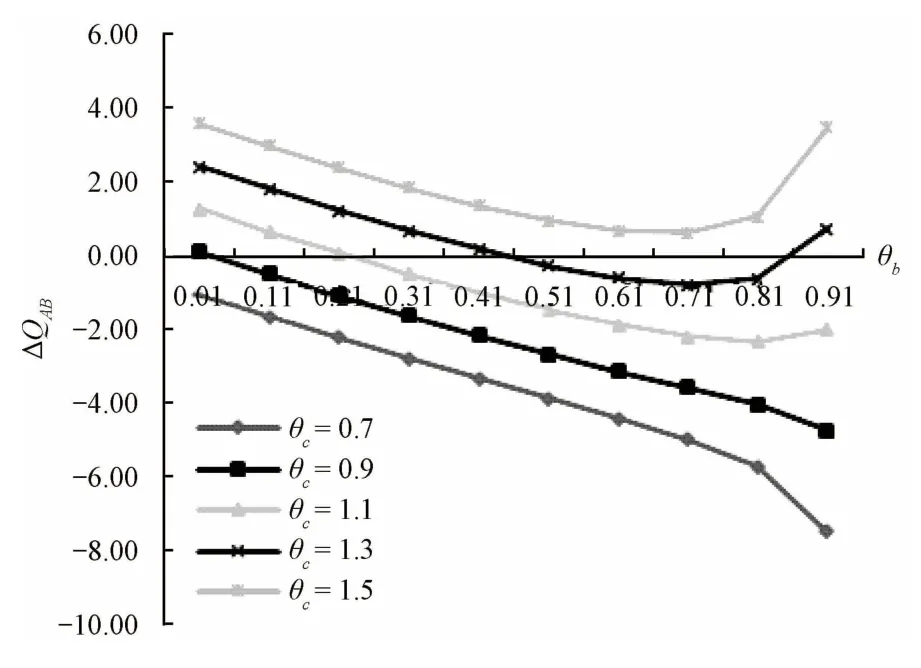
图5 参数b和c 关于ΔQAB 的敏感性分析

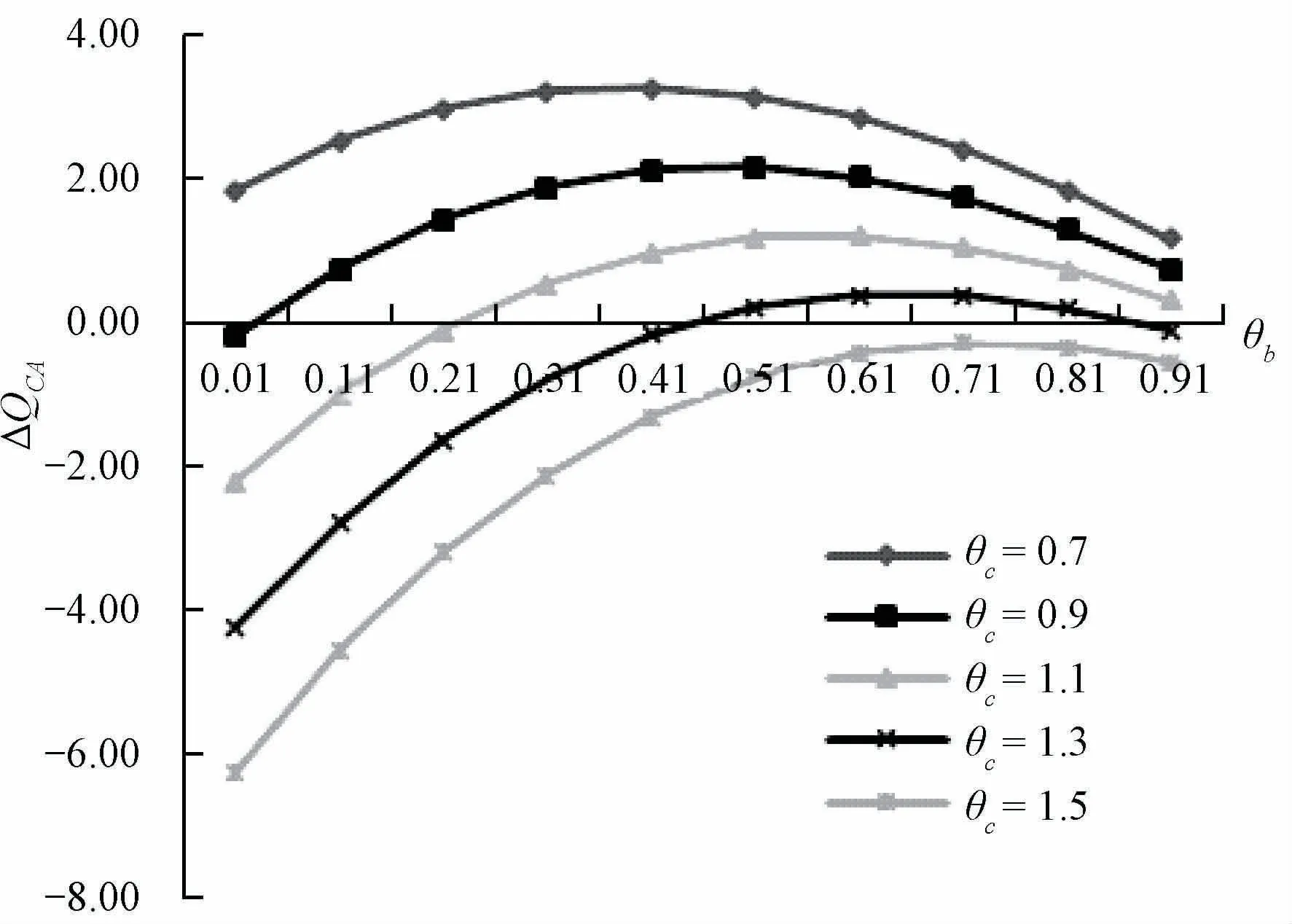
图6 参数b和c 关于ΔQCA 的敏感性分析

观察图5～7可知，ΔQAB和ΔQCB随参数b、c的变化趋势与Condition是一致的，而ΔQCA则相反。原因在于，当目标增量较大时，不管产品A、B之间的具体竞争关系如何，直接补贴消费者都将是最好的选择；而当目标增量较小时，总是应当在补贴A或B中进行选择。当Condition为负值时，意味着选择补贴企业A是较优的，对于ΔQAB和ΔQCB而言也是如此，而对于ΔQCA则恰好相反。

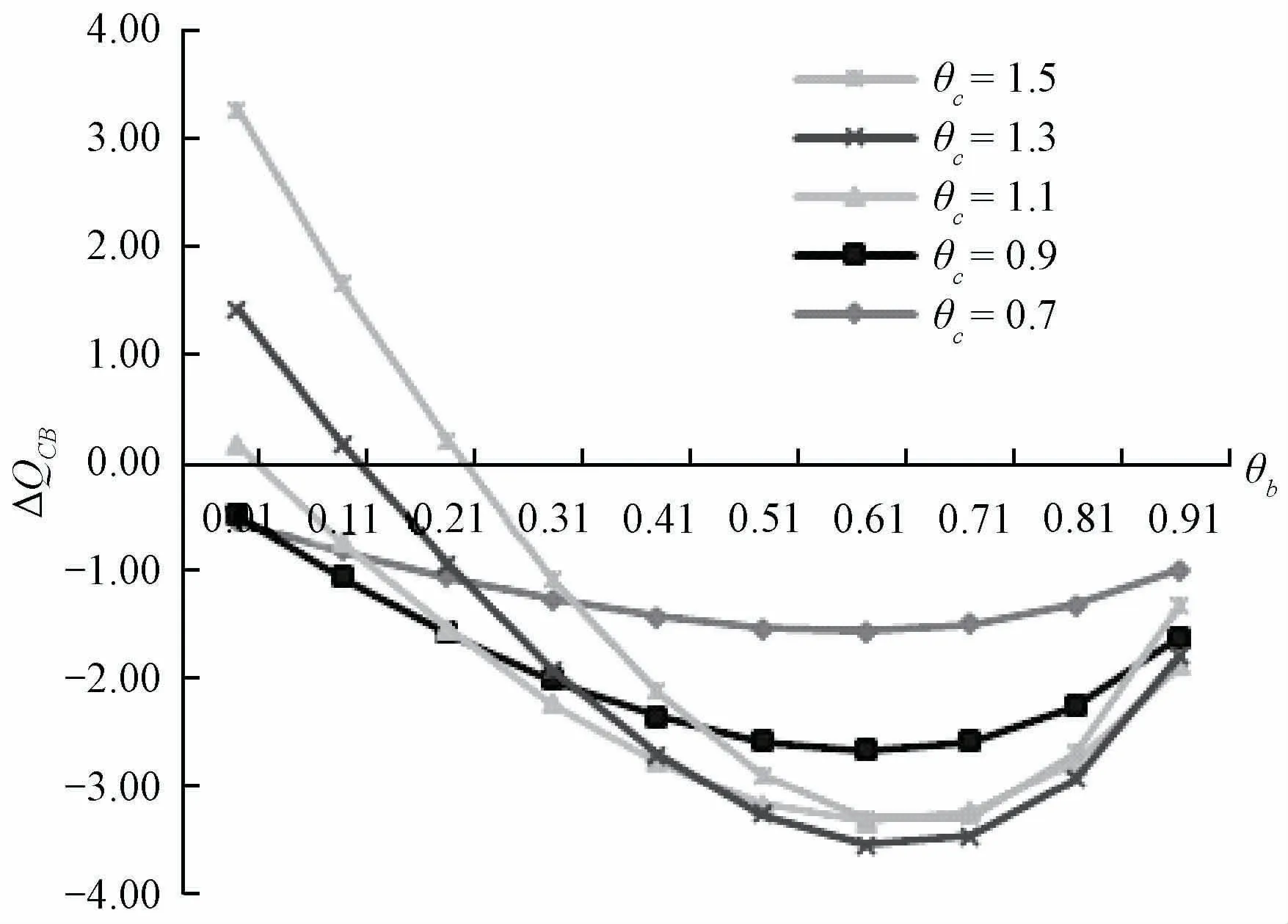
图7 参数b和c 关于ΔQCB 的敏感性分析

分析图6中的数据可知，当最优决策为先补贴企业A后直接补贴消费者时的目标增量门槛值随c B的增加而减小，随b B的增加先增加后减小。而图7中的结果则表明，当最优决策为先补贴企业B后直接补贴消费者时，目标增量的门槛值随c B的增加而增大，随b B的增加先减小后增大。上述观察结果与图5所呈现的结论相同，仅比较补贴企业A、B两种方式时，补贴企业B占优势的目标增量范围，亦随着c B的增加而增大，随着b B的增加先减小后增大。

4 结论

本文研究了在双寡头竞争情境下，以增加一定的总销售量的基础上最小化补贴总成本为目的时，如何在补贴企业和消费者中进行选择并制定相应的单位补贴额度。研究表明，在补贴方式选择上存在门槛策略，即当目标增量低于门槛值时，应当选择补贴给企业；而高于门槛值时，则应当直接补贴消费者。在不失一般性的情况下，假设企业A、B之间的产品替代性关系为b A≥b B。数值分析结果显示，当市场容量a相对较大，或两者替代性的差异程度中等、或产品B的成本相对较低时，应当选择先补贴企业A后直接补贴消费者的方式，反之则应选择先补贴企业B。同时，若根据市场参数环境，最优方式先补贴企业A后补贴消费者，则目标增量的门槛值随a的增加而增大，随c B的增加而减小，随b B的增加先增大后减小。而若最优补贴方式为先企业B后消费者，该门槛值的敏感性则与前者恰好相反，将随a的增加而减小，随c B的增加而增大，随b B的增加先减小后增大。

根据研究结果可知，在实践中，政策制定者首先应当对补贴产品相关信息进行调研，然后根据具体的市场环境参数、企业的具体运营情况以及补贴所期望达到的效果，参考上述研究结果，进行综合考量并制定相应情境下较优的补贴方式。

尽管混合补贴方式，即可以灵活选择多个补贴对象的方式，必将优于单一补贴方式，但是由于本文的目的在于较为深入地比较各补贴对象，分析其优劣及适用环境，为实践中补贴方案的制定提供一定的参考。同时，考虑到实践中混合补贴方式实施的难度，故集中讨论了单一补贴方式。若实践条件允许采取混合补贴方式时，研究结论同样可提供参考价值。如对产品A、B同时每单位补贴w C，将与对消费者每单位补贴w C有相同的效果。而且结论具有一定的可推广性，当市场中竞争的企业多于两家时，虽然在企业之间比较和选择时需要更多的讨论，但是先企业后消费者的整体框架不会改变。主要的局限性在于对市场竞争的刻画较为单一，因为考虑到面对的是需要拓展市场需求的产品，所以只讨论了线性需求假设下的双寡头竞争模型，未来可以作进一步拓展。同时，文中假设为确定性需求，若加上随机性，将对运营和管理带来新的思考和挑战，这也是后续需要展开的研究。