二重在线租赁问题的竞争策略及其风险补偿模型
徐维军,陈晓丽
(1.华南理工大学 工商管理学院,广州 510641;2.广东金融学院 互联网金融与信息工程学院,广州 510521))
在日常生产和生活中,租赁是一种常见的经济行为,作为一种仅次于银行信贷的重要融资方式,受到众多企业经营者的广泛关注。然而,科技的不断进步使得设备更新速度加快,再加上市场竞争日益激烈,以及企业对设备未来需求的不确定性,使得企业决策者只能在当前若干租赁信息的基础上立即做出决策,使决策者面临巨大的决策压力。租赁决策显示的这种在线特征为在线算法和竞争分析在这方面的应用提供了契机,使得租赁问题进入了更深层次的研究。
在线算法和竞争分析方法在在线租赁问题上的应用首次由Karp[1]提出,他以“雪橇租赁”为例介绍了在线问题及在线算法和竞争分析方法。一位滑雪爱好者去滑雪时需要使用雪橇,他可以选择一直进行租赁,并在每期支付租金1,也可以直接以价格p购买雪橇,那么,以后滑雪就不需要支付任何费用。若不知未来滑雪次数,则该问题被称为在线问题,反之为离线问题。Karp运用在线算法和竞争分析方法给出了最优在线策略:在前p-1期一直租雪橇,在第p期若还滑雪则购买雪橇。该策略的竞争比为2-1/p,即不管未来需求如何变化,在线成本最多是事后最优成本的2-1/p倍。该例被称为经典的雪橇租赁问题,由于与经济管理领域的设备租赁问题类似,故得到了租赁决策领域大量学者的青睐。此后,关于设备租赁问题的研究都是在雪橇租赁问题的基础上进行的扩展研究。考虑到资金的时间价值,El-Yaniv等[2]首次将利率引入到在线设备租赁问题中,运用在线算法和竞争分析方法得到了最优确定策略和最优随机性策略。考虑到现实生活中通货膨胀形势日益严峻,徐维军等[3]基于物价指数上涨因素给出了对应在线租赁问题的最优确定性和随机性算法,并通过数值分析说明通货膨胀因素对在线租赁决策的影响。除了利率和通货膨胀因素,折旧也是一个影响决策的不可忽视因素。张卫国等[4]考虑随机选择设备租赁或购买的方式,给出可折旧设备的最优在线租赁策略,并提出了转化随机策略,将随机选择多种获得设备的方式转化为随机选择两种获得设备的方式,并得到了相应的竞争比。王扬等[5]考虑二手货市场中出售价格与设备剩余价值之间的关系,分两种情况研究存在二手货市场的在线租赁问题。进一步,王扬等[6]从合同因素的角度进行研究,以非线性指数函数作为回购合同中的回购价格,建立了在线租赁模型,并给出了最优的竞争策略。考虑到以往研究均假设设备的使用寿命是无限的,马卫民等[7]研究了有限使用寿命情况下的设备租赁问题。此外,由于价格并不是永远不变的,Epstein等[8]研究了固定时长的雪橇租赁问题的各种变形,其中滑雪总天数和雪橇的购买价格固定,但是每天的租赁价格发生变化,并给出了租赁价格是任意变化、非增和非减变化情形下的最优在线算法。从市场信息角度,Fujiwara等[9]考虑未来市场需求输入服从指数分布,给出了平均意义上的最优竞争策略及其竞争比。从合作博弈角度,马卫民等[10]利用合作博弈理论从双人合作的角度研究了在线决策者与离线决策者的合作博弈模型,给出了最优竞争策略及双方合作分担成本时的纳什均衡解。
除了从上述角度进行分析外,部分学者也考虑了决策者的风险偏好,因为并不是所有的决策者都规避风险。Al-Binali[11]最早将竞争分析方法和概率假设综合起来,并引入在线决策者的风险偏好,提出了著名的风险补偿模型,指出投资者有时有目的的增加风险以期预测成功将获得更高的收益,即便预测失败,其风险也在决策者可接受范围内。进一步,许多学者在风险补偿模型的基础上进行了更深入的研究,如考虑投资者风险偏好的同时考虑利率[12]、通货膨胀[13]以及折旧[14]等因素。
此外,考虑到实际租赁市场中还存在除纯购买和纯租赁形式之外的多种可选租赁形式,Lotker等[15-16]研究了只有纯租赁和部分购买两种租赁形式下的随机算法,并推广到多租赁选择的决策问题,给出了最优随机策略及最优竞争比。Fujiwara等[17-18]通过求解多个租赁选择下的最优化模型,得到了确定性最优选择策略及最优竞争比下界,并讨论了包括纯购买在内的只有2种和3种租赁选择下的最优竞争比上界。另外,以可选租赁形式的个数为输入,给出了一个计算竞争比下界的算法,并得到了2~10 个租赁选择情况下具体的竞争比下界。
但是对于多种租赁选择情形,他们并未给出当租赁选择的数量确定时具体的竞争比表达式,更未考虑决策者的风险偏好。考虑到实际租赁活动中除纯租赁外,还可以先支付一部分费用,然后享受较优惠的租赁价格,类似于购买一张会员卡。因此,本文基于只有租赁和部分购买两种租赁选择情形下的在线租赁问题[15-16],提出二重在线租赁问题。并将投资者的风险偏好及对未来设备使用时长的概率预期引入,建立二重在线租赁问题的风险补偿策略,为多租赁选择下风险补偿策略的研究提供参考。
1 风险补偿模型
在在线租赁问题中,假设在线人有一个可选的策略集S={S(1),S(2),…},对于在线人给出的一个策略S(t)及离线对手发出的任何不确定输入σ∈Σ,其中Σ为离线对手发出的不确定输入序列集,记在线人决策策略的总成本为coston(σ;t),离线对手的设备租赁总成本为costoff(σ)。如果存在一个与σ无关的常数β,使得对于任何输入σ∈Σ均有coston(σ;t)≤βcostoff(σ)成立,则称策略S(t)是β竞争的。
令R(t)表示策略S(t)的竞争比,则有

设在线策略S(t)的风险 为λ(t),根据Al-Binali[11]的定义可知,λ(t)=R(t)/R*,即为策略S(t)的竞争比与最优竞争比的比值。设在线人的风险容忍度为λ(λ≥1),则在该风险容忍度下的可选策略集Iλ={S(t)|R(t)≤λR*}。而对于离线对手的不确定输入,风险偏好者往往有自己的预期,令F⊆Σ为风险偏好在线人的预期,如果预期成功,则得到的竞争比称为约束竞争比,记策略S(t)在预期F下的约束竞争比为
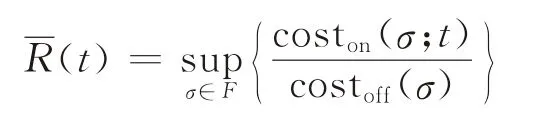
根据Al-Binali[11]关于预期成功时的风险补偿的定义可知,当F预期成功时,策略S(t)的风险补偿为。若在线人有多个预期Fi(i=1,2,…),则满足Fi∩Fj=φ(i=j)且∪Fi=Σ,每个预期Fi的概率为P i,且ΣPi=1。那么,在预期{(Fi,Pi)|i=1,2,…}下,策略S(t)的约束竞争比为。在概率预期{(Fi,Pi)|i=1,2,…}下,Al-Binali的风险补偿模型为:
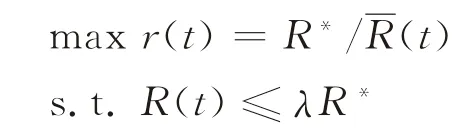
通过求解上述模型,就可以得到在一定概率预期下的最优决策时间。
2 问题陈述及确定性在线竞争分析
二重在线租赁问题:承租人在进行设备租赁时,有两种可选租赁方式:①直接在每一期以租赁价格r0进行租赁;②先支付一部分购买费用B,然后每期以较低的价格r1进行租赁。本文称这两种租赁方式分别为Fashion A 和Fashion B,面对未来设备使用时长的不确定性,承租人是选择Fashion A 租赁设备还是Fashion B 租赁设备,或者是先采用Fashion A 租赁设备一段时间后再用Fashion B 租赁设备,哪种方法最为划算?
为了方便,将上述二重在线租赁问题简记为Fashion A-B。在Fashion A-B中,假设T为总的设备使用时间,则最优离线成本函数为

式中,T*为离线对手采用Fashion A 或Fashion B的临界时间点,令Fashion A 和Fashion B 产生的成本相等,即r0T*=B+r1T*,可得T*=B/(r0-r1)。这里假设T*≥1,即B-r0+r1≥0;否则,Fashion B永远优于Fashion A,承租人也不会选择Fashion A,即退化为只有一种租赁方式可以选择的租赁问题,此处不作考虑。
设在线承租人采取的策略S(t)为:在前t-1期采用Fashion A 进行租赁,第t期开始采用Fashion B进行租赁。记在线策略S(t)的成本为

根据式(1)、(2),并根据竞争分析方法和在线算法,可得策略S(t)关于T的竞争比为
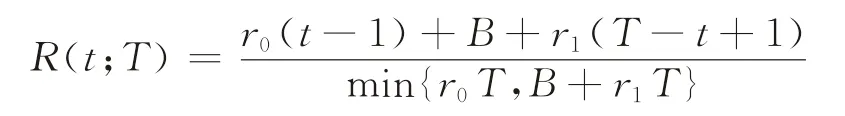
下面分两种情况进行讨论:
(1)当t<T*时,由于r0>r1,故当T<T*或T≥T*时,R(t;T)关于T单调递减。此外,经计算知,那么,R(t;T)关于T连续,所以当T≥t时,R(t;T)关于T单调递减,离线对手为了使竞争比达到最大,对策略S(t)做出的最优选择是T=t,则可得竞争比:

易知,R1(t)关于t单调递减,那么,在线人为了使竞争比达到最小,会选择t=T*-1,则此时的最优竞争比为R1(T*-1)。
(2)当t≥T*时,由于T≥t,故
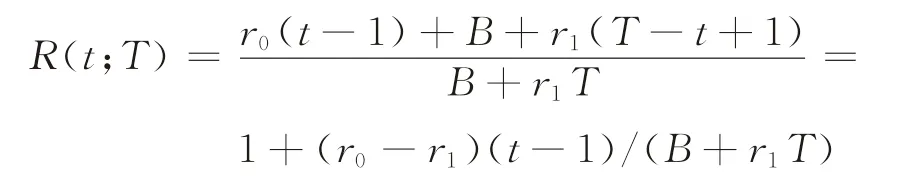
关于T单调递减,离线对手为了使竞争比达到最大,对策略S(t)做出的最优选择是T=t,因为T=t≥T*,所以costoff(t)=B+r1t,则可得竞争比:
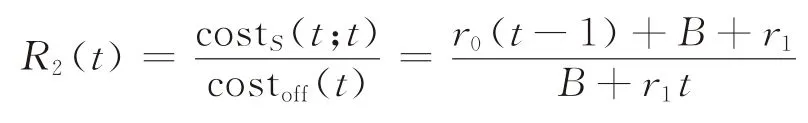
容易验证,R′2(t)>0,即R2(t)关于t单调递增,那么,在线人为了使竞争比达到最小,会选择t=T*,则此时的最优竞争比为R2(T*)。
因为
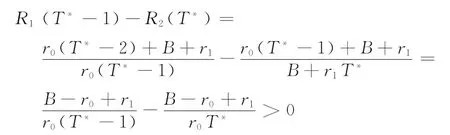
所以,在线人为了得到最小的竞争比而选择t=T*及策略S(T*),得到最优竞争比为
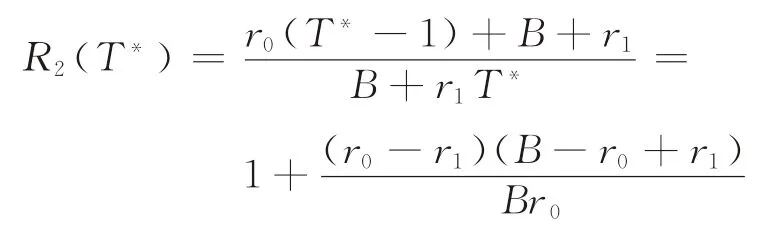
则有如下定理成立:
定理1在有Fashion A 和Fashion B 两种租赁方式的二重在线租赁问题中,最优在线策略为:前T*-1期采用Fashion A 进行租赁,在第T*期开始采用Fashion B 进行租赁,即最优决策时间为T*。由此得到最优竞争比为
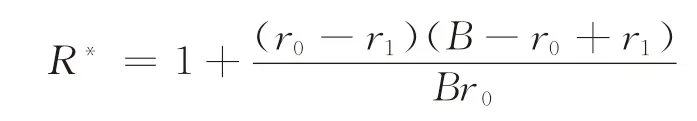
其中:r0为Fashion A 的租赁价格;B为Fashion B的部分购买价格;r1为对应的租赁优惠价格;T*=B/(r0-r1)。
通过定理1可知,在二重在线租赁问题中,在线决策者采用策略S(T*)能够达到最优的竞争比,花费的成本最多是最优离线决策者成本的1+(r0-r1)(B-r0+r1)/(Br0)倍。此外,一方面,当r1=0时,二重在线租赁问题就转化为经典的雪橇租赁模型;另一方面,通过定理1可知,当r1=0时,二重在线租赁问题的最优竞争比为R*=2-r0/B,且最优决策时间T*=B/r0,与经典的雪橇租赁问题一致。由此说明,本文给出的二重在线租赁问题是经典雪橇租赁问题的一种自然地推广。
3 风险补偿策略
在本节中,将风险补偿模型引入到二重在线租赁问题中,给出两种概率预期下的最优决策时间和最优竞争比,为风险偏好投资者提供一个最优的竞争策略。
假设预期F1={T:T<T*}和F2={T:T≥T*}的概率分别为P1和P2,其中,P1+P2=1,在线承租者的风险容忍度为λ,且λ≥1。根据定义可知,在风险容忍度λ下的可选策略集

在预期{(F1,P1),(F2,P2)}下,策略S(t)的约束竞争比为
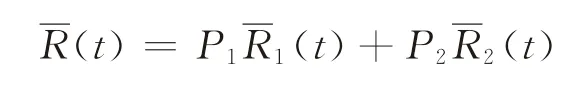

通过求解上述模型,即可得到最优的决策时间,从而得到最大的风险补偿。
定理2给定风险容忍度λ(λ≥1),当预期F1={T:T<T*}和F2={T:T≥T*}的概率分别为P1和P2时,策略S(t)的最优风险补偿为最优决策时间为

其中,t1、Δ和函数的表达式参见证明过程。
证明首先,根据R(t)≤λR*计算出风险容忍度λ下的可选策略集Iλ。
(1)当t<T*时,有
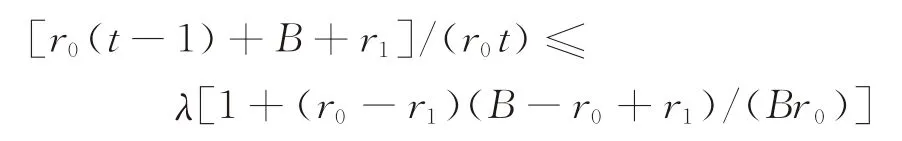
通过求解可得

通过比较可知,t1≤T*,则此时的可容忍策略集I1={S(t)|t1≤t<T*}。
(2)当t≥T*时,有
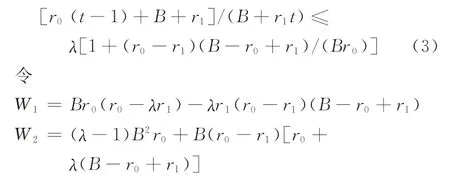
则式(3)可转化为W1t≤W2,易知,W2≥0。通过求解可得,当W1>0 时,式(3)的解为T*≤t≤此时的可容忍策略集

当W1≤0时,不等式W1t≤W2恒成立,此时的可容忍策略集I3={S(t)|t≥T*}。
综合(1)、(2)可知,当W1>0时,在风险容忍度λ下的可选策略集

当W1≤0时,在风险容忍度λ下的可选策略集

然后,计算在预期{(F1,P1),(F2,P2)}下,策略S(t)的约束竞争比为

最后,求解在预期{(F1,P1),(F2,P2)}下的风险补偿模型:
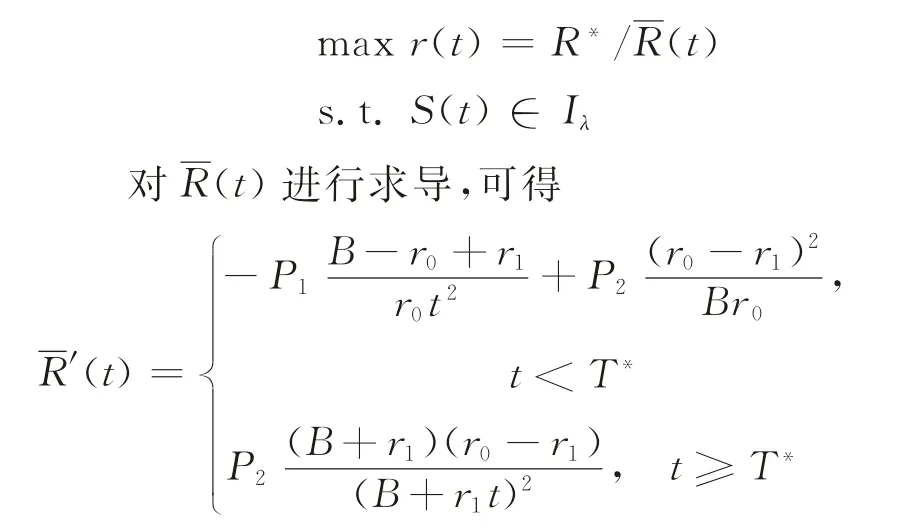
由此可知,当t≥T*时单调递增,在t=T*时取得最小值。接下来讨论当t<T*时的单调性。令
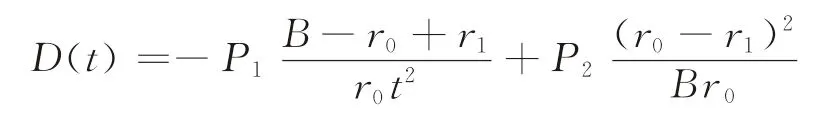
易知,当t>0时,D(t)单调递增,令D(t)=0,可得
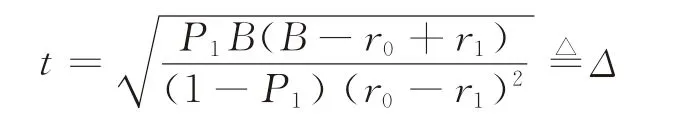
则当0<t<Δ时,D(t)<0;当t>Δ时,D(t)>0。则:①当Δ≥T*,即时,在t1≤t<T*时单调递减;②当Δ<T*,即时,若t1<Δ,则在t1≤t<Δ时单调递减,在Δ≤t<T*时单调递增;若t1≥Δ,则在t1≤t<T*时单调递增。根据关于t的单调性可得图1~3。
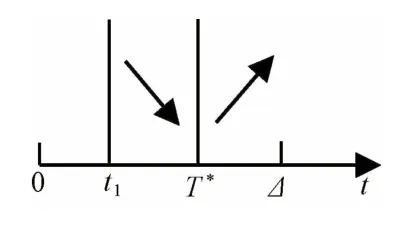
图1 Δ≥T*时(t)的单调性
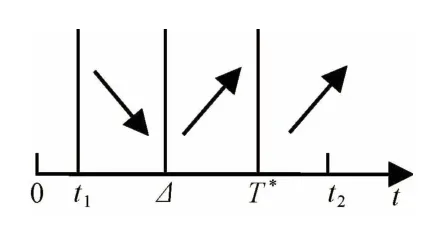
图2 t1<Δ<T*时(t)的单调性
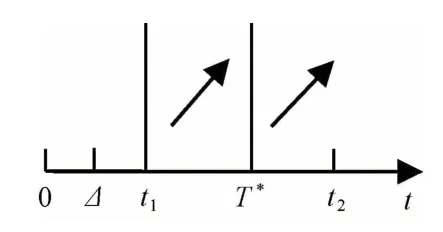
图3 Δ≤t1时(t)的单调性
根据图1可知,当t<T*时在t=T*-1处取得最小值;而当t≥T*时在t=T*处取得最小值。又因为当P1≥B/(2B-r0+r1)时,,所以,此时的最小值在t=T*处取得。根据图2可知,当t1<Δ<T*时,的最小值在t=Δ或T*处取得,即为。根据图3 可知,当Δ≤t1时,的最小值在t=t1或T*处取 得,即为。综上可知,在预期{(F1,P1),(F2,P2)}和风险容忍度λ下,策略S(t)在t*处的补偿收益达到最大,即最优决策时间为t*,最大的补偿收益为
推论1给定风险容忍度λ(λ≥1),当预期F1={T:T<T*}的概率为1时,最优决策时间为t=T*,最优的风险补偿为r(T*)=R*;当预期F2={T:T≥T*}的概率为1时,最优决策时间为t=t1,最优的风险补偿为
4 算例分析
根据前面分析得到的概率预期下的风险补偿模型,本节将通过算例进一步说明风险容忍度和概率预期的引入对最优约束竞争比和收益补偿的影响。假设某公司需要使用一块场地用来做产品宣传,但是需要根据产品销售绩效来决定何时结束宣传,也即公司并不能确定场地的具体使用时长,租赁方给出两种租赁选择:①以每天200元的价格进行租赁;②支付2 000元的预付款,然后以每天150元的价格进行租赁。那么,承租公司应该采取怎样的策略才是最优的? 另外,如果承租公司的决策者是一个风险偏好者,那么,又要如何进行决策? 针对该问题,可以采取本文给出的风险补偿策略,对应的参数取值为:r0=200,r1=150,B=2 000。则有T*=40,确定性策略的最优竞争比R*=1.243 75。设公司决策者的风险容忍度为λ,对总时间的预期有F1={T:T<T*}和F2={T:T≥T*},相应的概率分别为P1和1-P1。表1即是根据决策者的风险容忍度和概率预期得到的对应最优决策时间t*和补偿收益r(t*)。同时,为了说明有预期时的最优约束竞争比相对于无预期时的最优竞争比有所改善,参考文献[12],采用表示当预期成功时获得的最优约束竞争比相对于确定性最优竞争比R*的改善幅度。
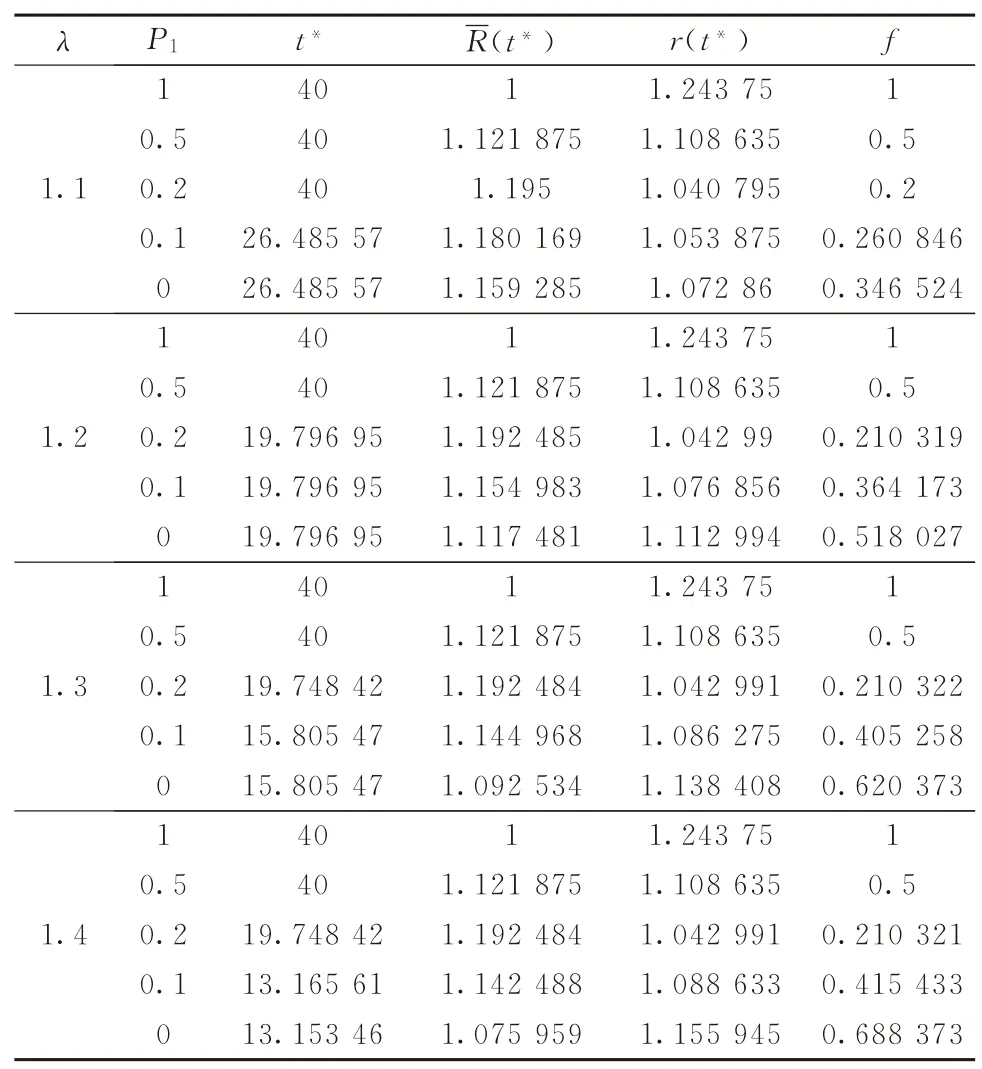
表1 不同风险容忍度和概率预期下的风险补偿策略
根据表1可知,在给定的风险容忍度λ下,最优决策时间不迟于无预期时的最优决策时间,有概率预期时的竞争比均小于无概率预期时的竞争比R*,如果预期成功,则可得风险补偿r(t*)>1。特别地,当预期F1={T:T<T*}的概率P1=1时,如果预期成功,则在线决策者的成本不会低于离线决策者的成本,该预期下的约束竞争比为=1。此外,在相同概率预期下,随着风险容忍度的增大,得到的最优约束竞争比逐渐减小,得到的收益补偿也逐渐增大,相应竞争比的改善幅度也逐渐增大,如P1=0.1时,随着风险容忍度λ从1.1变化至1.4,收益补偿从1.054增加至1.089,最优竞争比的改善幅度也从26.08%增加至41.54%。这说明,在相同概率预期下,决策者的风险容忍度与他得到的风险补偿成正比。
5 结语
Karp[1]的“雪橇租赁”问题作为运用在线算法和竞争分析方法研究在线设备租赁的经典问题,仅仅假设决策者有两种获得设备的方式,一种是纯租赁方式,另一种是直接购买设备的方式。而在现实租赁市场中,有很多种设备设施租赁方式,所以研究其他租赁方式下的最优租赁策略是很有必要的。本文考虑了纯租赁和支付部分购买费用后再租赁这两种租赁方式,利用在线算法和竞争分析方法得到确定性最优在线策略,并给出了最优竞争比。此外,考虑到决策者并不都是风险厌恶的,他们往往更希望利用风险获得更高的收益;再者,决策者往往可以根据经验或市场其他信息对设备使用时长进行预期。因此,本文将决策者风险容忍程度及投资者的概率预期引入在线算法中,得到了二重在线租赁问题的风险补偿模型。并通过算例分析,说明风险容忍度的引入能够提高策略的竞争性能,而且当决策者对总的设备使用时间的预期正确时,决策者能够获得一定的补偿收益。
然而,本文并未考虑市场上其他因素的影响,如通货膨胀、利率、设备折旧等因素。另外,本文仅考虑了两种不同租赁方式下的风险补偿策略,对于多种不同租赁方式下的风险补偿模型还有待研究。

