基于混沌理论的企业动态能力、投资和收益的非线性关系

盛永祥，王旭娜，吴洁

（江苏科技大学 经济管理学院，江苏 镇江 212003）

近年来，越来越多的学者开始关注动态能力，动态能力是企业核心竞争优势的关键，动态能力的投入水平与企业的投资和收益息息相关。企业如何制定合理的动态能力投入水平以及合理的投资决策，进而使收益增加并赢得市场竞争优势成为一个值得研究的问题。

许多学者从不同角度给出了动态能力的定义，本文采用Teece等[1]给出动态能力定义：“动态”是指为了与动态变化的外部环境保持一致，企业延续或重构自身胜任力的能力；而“能力”则强调了战略管理在正确处理、整合和重构企业内外部知识、资源和技能以匹配变化的环境需求中的关键作用。

动态能力的提高来自于组织对动态能力的投入，这其中的投入不仅包括资金投入，而且还包括时间投入、人力投入、精力投入等方面[2]。许多学者研究了动态能力、投资与收益两两之间相互促进、相互制约的关系。动态能力能够促进收益增加，随时间变化的动态能力的发展与收益成正比[3]。在企业发展早期，当其动态能力相对薄弱时，对单位动态能力投入的增加可以促进收益增加[4]；当企业的动态能力已经达到同行业比较高的水平时，需要注意把动态能力转化为有利于收益提高的生产、销售等其他环节，此时再加大对单位动态能力的投入力度会起到与收益增加相悖的结果[5-7]。对动态能力投入量不当一方面可能会造成资源浪费，另一方面也可能导致产生许多无效创新及科技成果转化率低下，这些对于企业都是不利的[8]。

投资增加会促进动态能力发展[9]，当投资量达到一定值时，过多的投资反而对动态能力的发展有一定的抑制作用[10-11]。投资发展速度在其峰值到来之前很快，峰值之后逐渐变缓。企业发展早期需要大量的投资，达到峰值后投资对收益的影响会逐渐变缓，即当组织意识到已经达到行业收益最高点后会适当地降低在这方面的投资[12-13]。假定一个企业的资源是有限的，企业长期在动态能力上过度投入必然会导致在其他方面的投资有所减少。投资和收益之间是双向因果关系，投资对收益增加有促进作用，但投资量不当也会阻碍企业收益增加[14-15]。从总体上看，上述研究主要采用实证分析的方法来研究影响动态能力、投资和收益的因素以及各因素之间的相互关系，而缺乏动态能力和投资对收益影响程度的研究。

本文通过企业动态能力、投资与收益之间的关系分析，构建了三者之间相互关系的非线性行为方程。数值仿真分析了方程中参数变动对企业收益的影响，得到了动态能力、投资和收益三者之间非线性演化的混沌吸引子和不同情形下的动态演化图。结合联想集团有限公司的实际数据进行分析，提出了相关建议和对策。本文的研究与以往文献研究的不同之处主要体现在：

（1）以往文献大多数单纯从能力或投资的角度研究其对企业收益的影响，且相关变量之间多属于线性关系，未能考虑动态能力和投资如何综合作用影响企业收益；而本文综合考虑了动态能力、投资和收益之间的关系，构建的三者之间的非线性演化模型能够更好地分析动态能力和投资综合作用对企业收益的影响。用混沌理论分析动态能力、投资和收益的非线性关系能够很好地表现出各变量之间的相互联系，丰富了该领域中对新方法的应用和研究。

（2）以往文献对动态能力、投资和收益的研究主要采用实证分析的方法研究三者的影响因素以及各因素之间的相互关系；而本文建立了动态能力、投资和收益演化的数学模型，能够定量分析动态能力和投资对企业收益影响程度的大小，在理论上为相关研究提供了一个新的视角和研究思路。

（3）以往文献研究动态能力或投资对企业收益的影响主要集中于静态分析，却忽略了两者对企业收益的影响会随时间的变化有所不同；而本文构建的动态能力、投资和收益之间的演化模型能够捕捉动态能力和投资在不同时间段对企业收益的不同影响，有助于满足企业制定合理的投资策略和动态能力投入策略，具有较为重要的实际应用价值。

1 动态能力投资模型建立

动态能力的开发利用不仅可以提高企业的竞争能力，而且还可以在企业投资水平不变的情况下提高收益率，非常适合当前创新驱动发展经济的要求。构建动态能力约束下的投资收益系统，进一步深入分析动态能力在投资收益系统中的演化影响，是解决企业以合理的投资水平达到收益率最大化的关键问题所在。根据上述文献对企业动态能力、投资和收益的相关研究，在二维投资收益系统中，加入动态能力更加贴近实际，符合创新驱动经济的发展要求。加入动态能力的三维投资收益系统为：

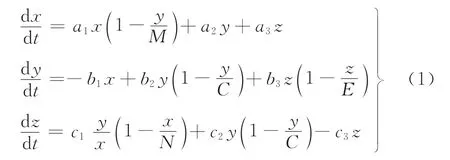
式中：a1、a2、a3、b1、b2、b3、c1、c2、c3、M、C、E、N均为大于0的常数。其中，各个参数的意义如下：

x（t）——企业动态能力

y（t）——企业投资

z（t）——企业收益

a1——企业动态能力的发展系数

a2——投资对动态能力的影响系数

a3——收益对动态能力的影响因子

b1——动态能力对投资的影响系数

b2——投资发展速度的弹性系数

b3——上期收益对下期投资的影响系数

c1——动态能力投资力度对收益的影响系数

c2——投资对收益的影响系数

c3——动态能力等的投入对收益的抑制系数

M——投资对动态能力影响的转折点

C——一个经济时期内投资的峰值

E——一个经济时期内收益的峰值

N——动态能力对收益影响的转折点

式（1）中，第1个公式表示随时间变化的动态能力x（t）的发展与收益z（t）成正比。投资y（t）的增加会促进动态能力x（t）的发展。当y（t）到达一个峰值时，过多的y（t）反而对x（t）的发展有一定的抑制作用。对于a1x（1-y/M），当y＜M时，即（1-y/M）＞0时，动态能力的发展速度增快；当y＞M，即（1-y/M）＜0时，动态能力的发展变缓。第2个公式表示投资y（t）发展在其峰值C到来之前很快，峰值到来之后逐渐变缓。收益z（t）发展早期会需要大量的投资，达到峰值E后对投资y（t）的影响会逐渐变缓。动态能力x（t）的发展可以适当地减轻企业对投资y（t）的依赖。对于b2y（1-y/C），当y＜C，即（1-y/C）＞0时，投资y（t）发展速度加快；当y＞C，即（1-y/C）＜0时，投资y（t）发展速度变缓。对于b3z（1-z/E），当z＜E，即（1-z/E）＞0时，收益z（t）对投资y（t）的影响是正向的；当z（t）发展到一定规模，即达到一个峰值E后，z（t）对y（t）的影响开始变为负向的，即当组织意识到已经达到行业收益最高点后会适当地降低在这方面的投资。第3个公式表示动态能力x（t）通过投资y（t）对收益z（t）产生影响，y/x表示对单位动态能力的投入，当x＜N，即（1-x/N）＞0时，表示y/x的增加，即对单位动态能力投入的增加对收益z（t）有促进作用；当x＞N，即（1-x/N）＜0时，表示y/x的增加，即对单位动态能力投入的增加对收益z（t）有抑制作用。投资y（t）最初对收益z（t）有促进作用，当投资达到一定的峰值C后开始对收益z（t）有一定的阻碍作用。

2 动态能力投资模型平衡点及稳定性分析

根据Hurwitz的雅可比矩阵可以判断系统平衡点是否稳定，式（1）的雅可比矩阵为

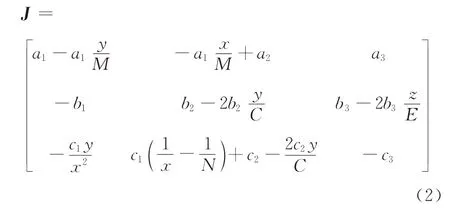
式（1）是非常复杂的动力系统，a1、a2、a3、b1、b2、b3、c1、c2、c3、M、C、E、N取不同的值，会出现不同的动力学行为。经过调试和数值仿真后发现，当式（1）取如下参数时展示出非常好的动力学行为，即：

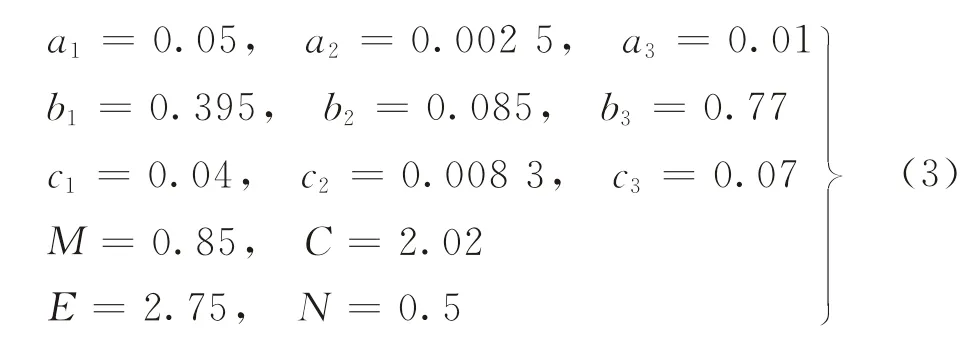
通过计算得出式（1）有4个实平衡点，分别为：

固定该模型的系数如式（3），计算得在s1处的雅可比矩阵的特征值为

所有的特征值的实部均小于0，因此，s1为稳定鞍点；在s2处的雅可比矩阵的特征值为

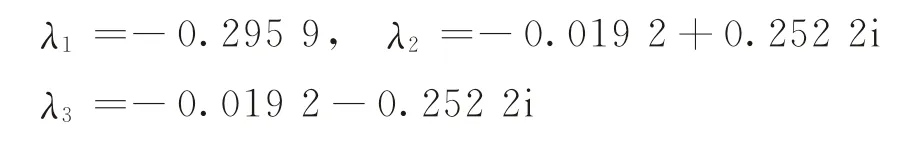
所有的特征值的实部都小于0，因此，s2为稳定鞍点；在s3处的雅可比矩阵的特征值为

不是所有的特征值的实部均小于0，因此，s3为不稳定鞍点；在s4处的雅可比矩阵的特征值为

不是所有的特征值的实部都小于0，因此，s4为不稳定鞍点。

3 情景分析

动态能力、投资以及收益之间相关参数的变化可能引起复杂的混沌现象，经过数据调试和数据分析，选取了能够较好地表现系统变化趋势的参数和初值，发现动态能力约束下的投资收益吸引子以及动态能力、投资和收益之间的演化规律。

3.1 系统混沌现象分析

李雅普诺夫指数[16]是用来度量运动对初值的敏感程度的量，若最大李雅普诺夫指数大于零，就会有混沌现象存在。固定系统的参数如式（3），取初值[0.05，0.523，0.24]，此时相应的李雅普诺夫指数图如图1所示。

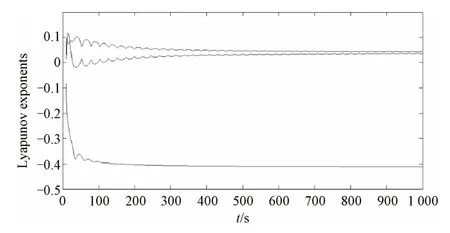
图1 李雅普诺夫指数图

可见，此时系统有正的最大李雅普诺夫指数，因此，系统有混沌存在。这时可以得到一个混沌吸引子，本文称为动态能力约束下的投资收益吸引子，如图2所示。

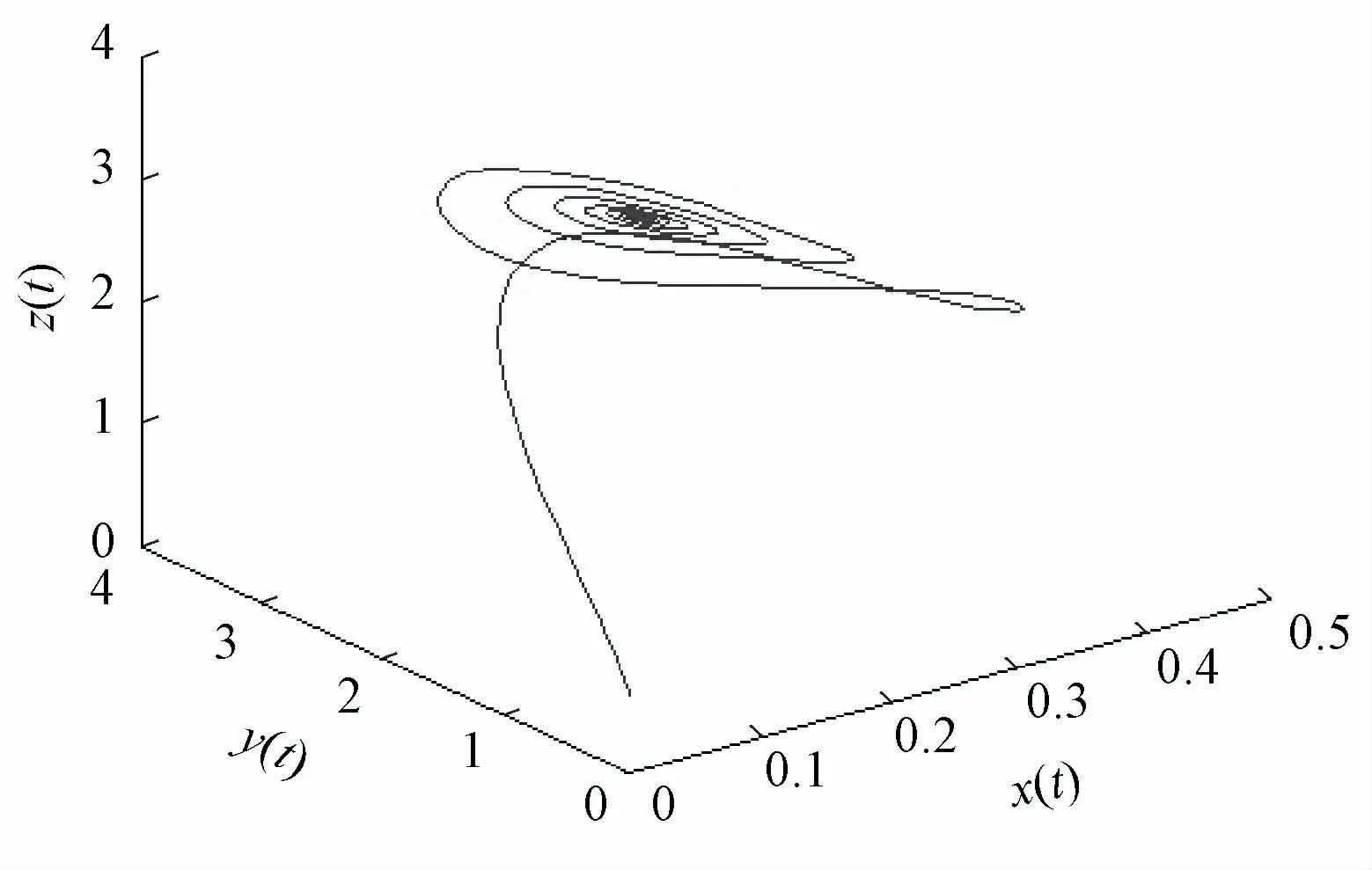
图2 投资收益吸引子

随着时间的增加，系统的轨线进入了如图2所示的圆饼状的结构中，即动态能力、投资和收益之间的关系此时呈现出无序的混沌状态。

系统相图在二维平面的投影可以更为详尽地了解系统轨线的运动规律，图3～5显示了吸引子的二维图。由图3～5可以看出，动态能力、投资和收益两两之间的关系在初始状态下是正相关的，即动态能力增加促使投资增加，动态能力增加促使收益增长，投资增加也促进了收益的增长。但是一段时间后系统各个变量之间不再是简单的正相关或是负相关，而是会呈现出不规则的循环现象。

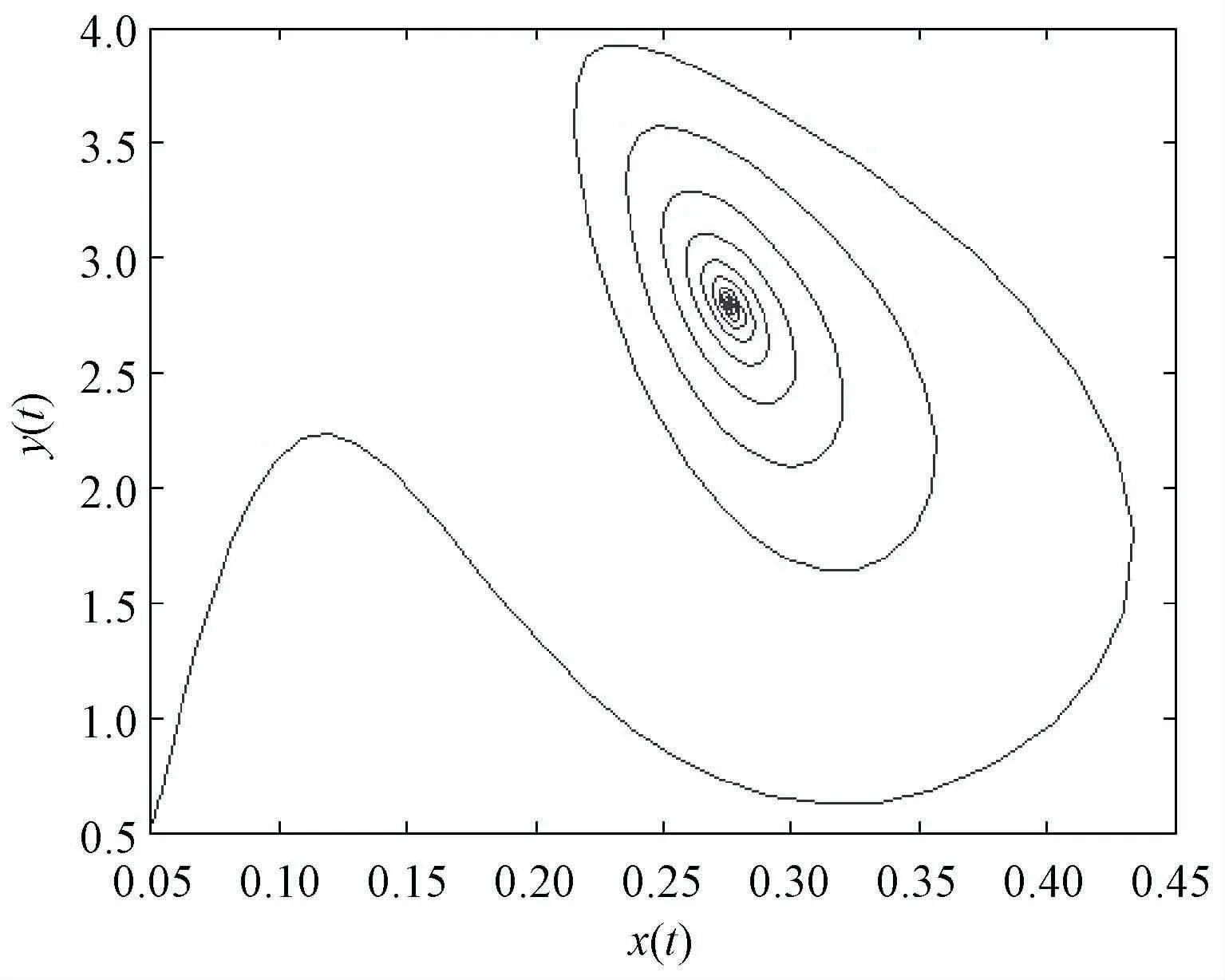
图3 投资收益吸引子关于x-y 的二维图

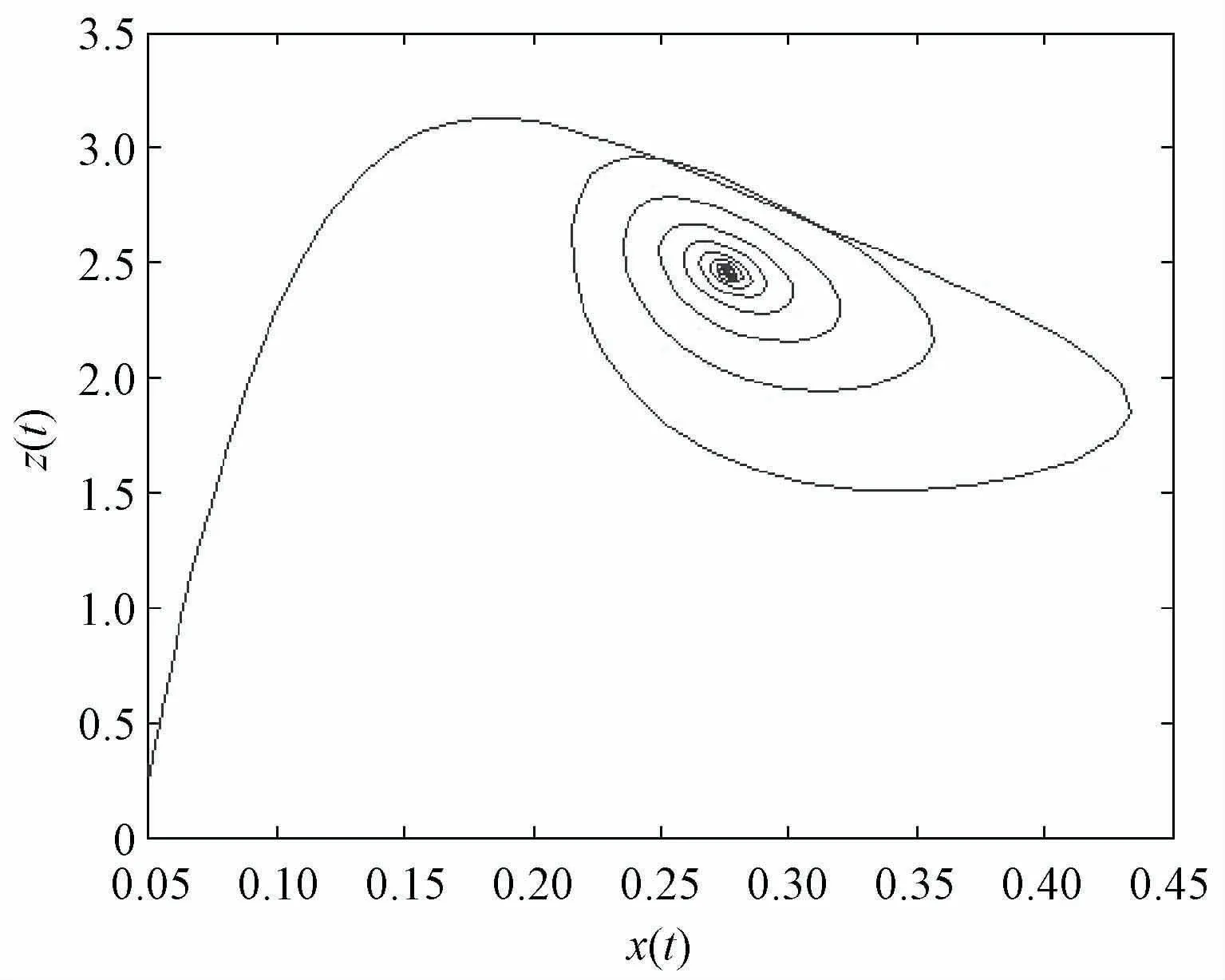
图4 投资收益吸引子关于x-z的二维图

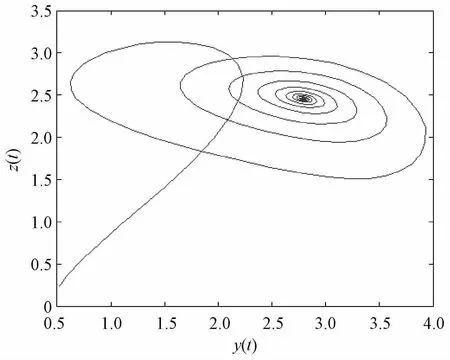
图5 投资收益吸引子关于y-z的二维图

式（1）的时间演化历程如图6所示。系统的时间序列图能够很好地观察变量是否随时间变化而呈现某种趋势，还可以很好地反映系统运行的频率和振幅，图6显示了x（t）、y（t）和z（t）的时间序列图。由图6可以看出，企业投资和收益在期初会出现剧烈的震荡现象，随着时间的增加振幅越来越小，后期逐渐趋于稳定。企业动态能力在期初出现轻微震荡现象，随着时间增加振幅越来越小，最后基本趋于平稳。

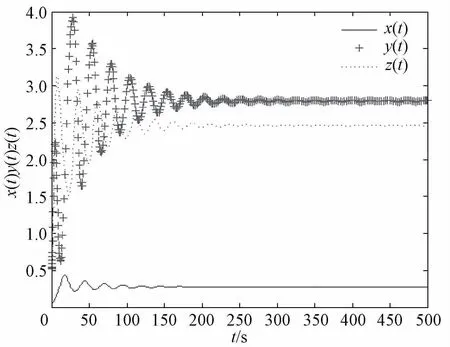
图6 系统关于t-xyz的时间序列图

由上述分析可以看出，在系统参数给定情况下企业动态能力、投资以及收益会呈现出非周期的循环现象。动态能力、投资以及收益在期初均会呈现一定程度的震荡现象，投资的振幅最大，收益的振幅次之，动态能力的振幅最小，随时间增加三者的振幅最后基本趋于平稳。

3.2 对参数和初值敏感依赖性分析

混沌系统的一个显著特征就是系统对参数和初值有很强的敏感依赖性，一个参数或初值的变化都可能对结果产生巨大影响[17]。固定其他参数和初始条件不变，令a3=0.072，此时系统轨线发生改变，如图7～10所示；系统的时间序列图也发生了改变，如图11所示。

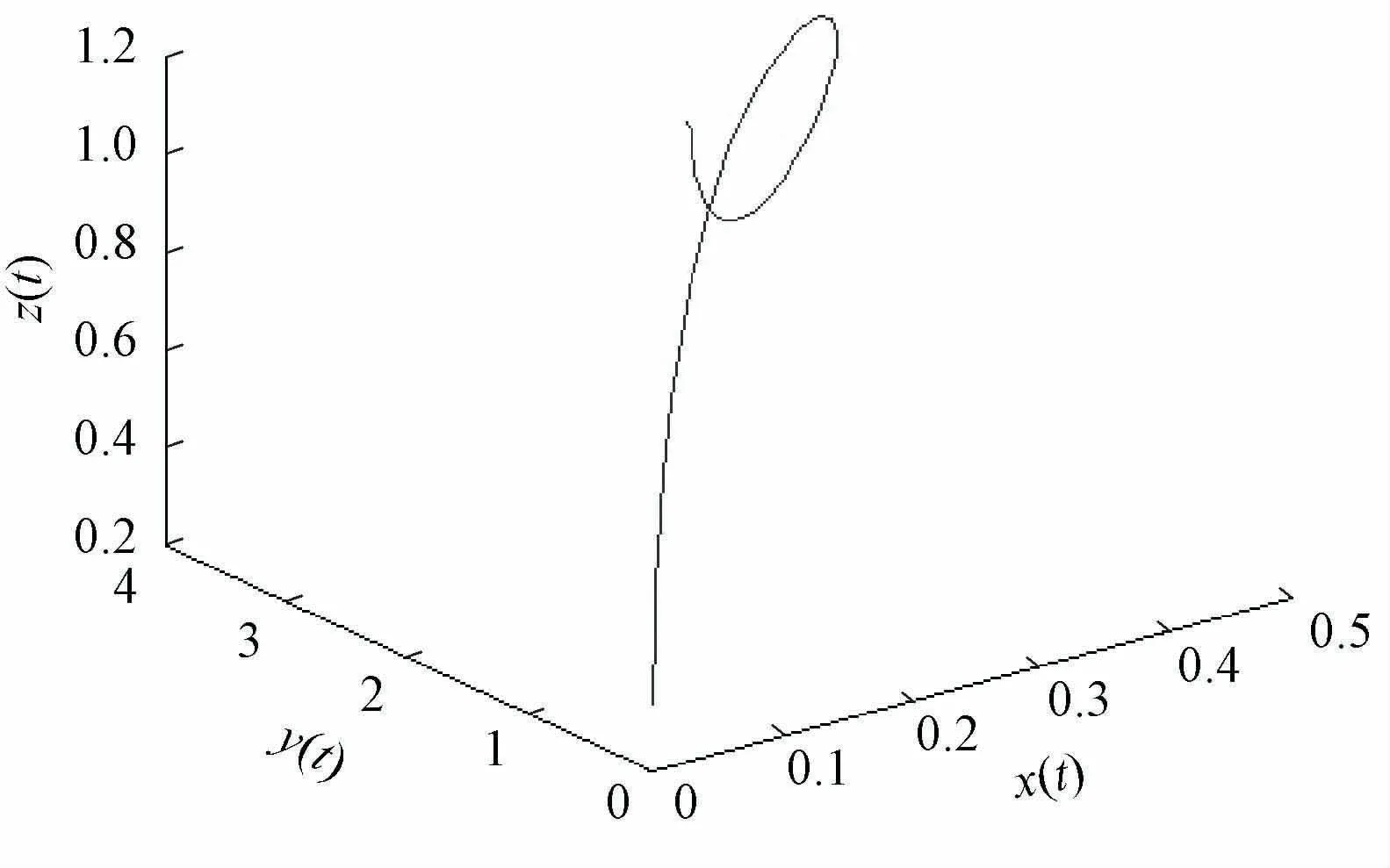
图7 a3改变后的投资收益吸引子

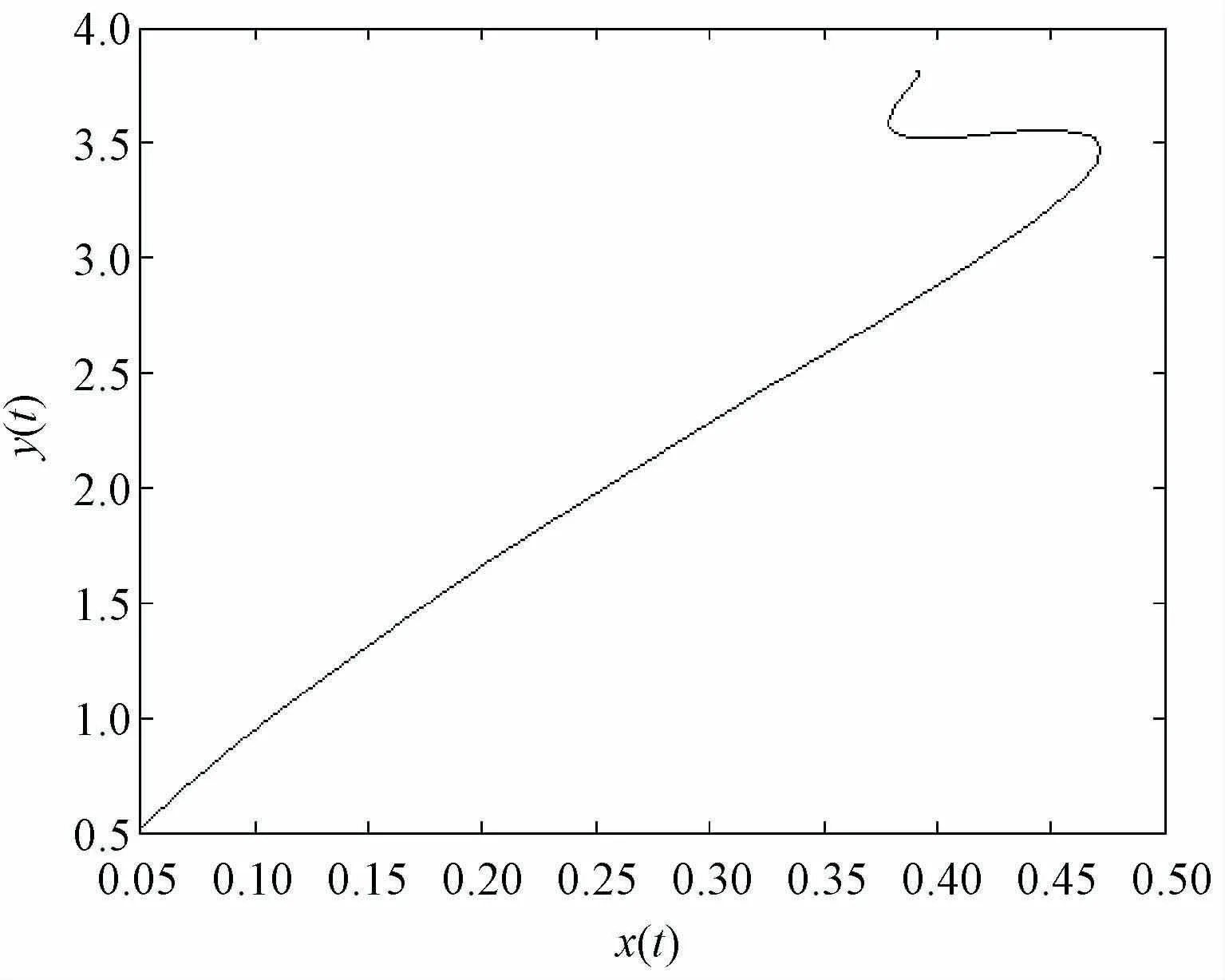
图8 系统关于x-y 的二维图

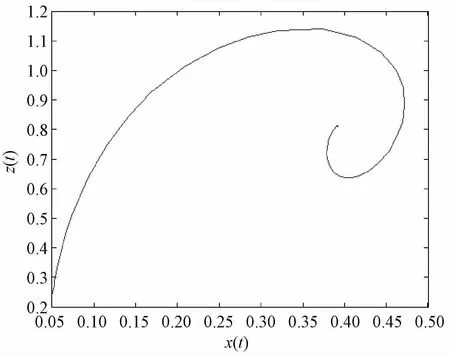
图9 系统关于x-z的二维图

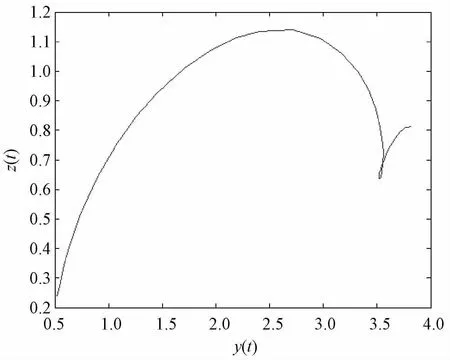
图10 系统关于y-z的二维图

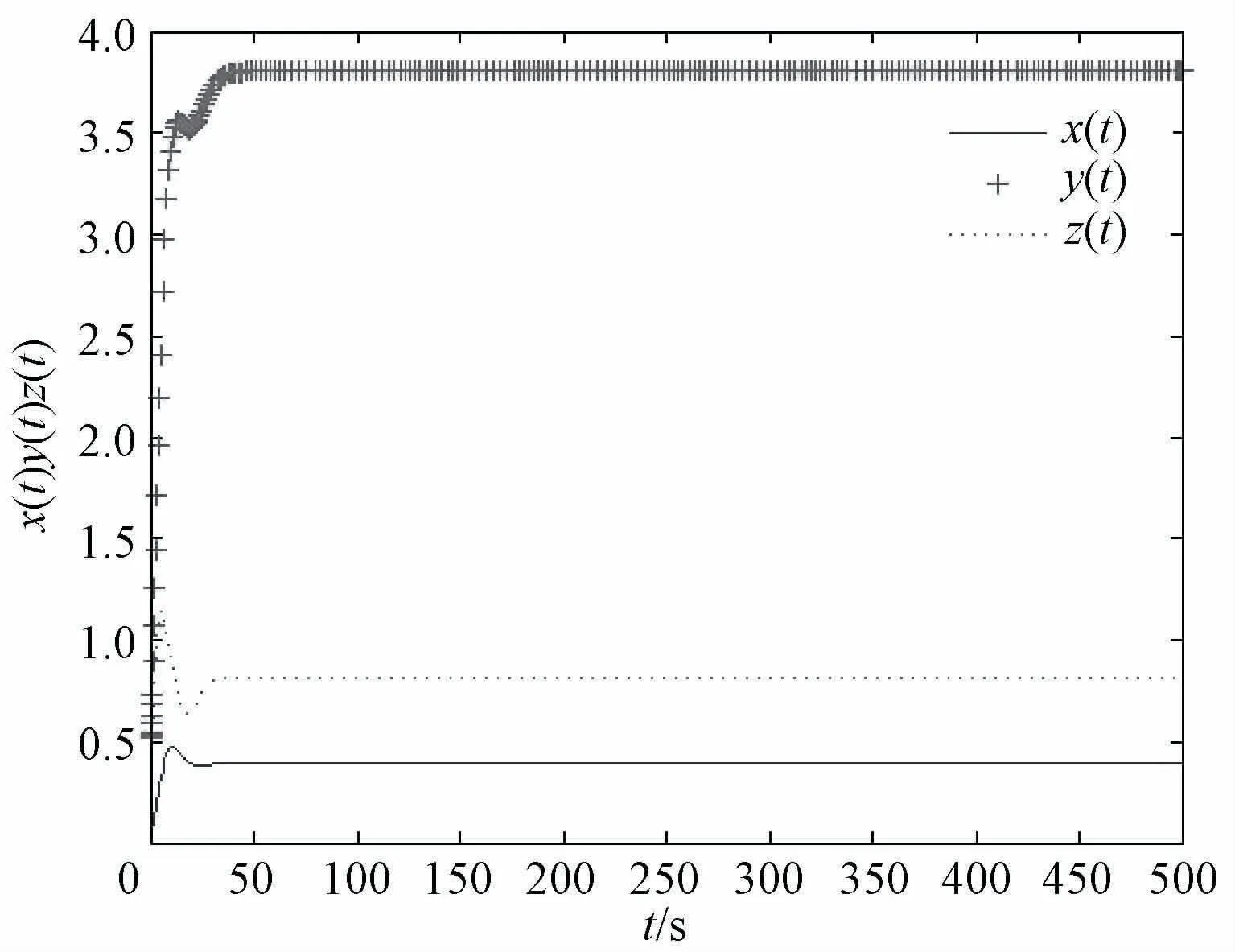
图11 系统关于t-xyz的时间序列图

此时，系统的轨线呈现出如图7所示的圆勺形状。对于图8，在x（t）、y（t）均较小时是近似线性的，说明在此参数范围内，动态能力和投资的增长是正相关的；后期随着投资的增长，动态能力出现了迂回的现象，即后期投资增加，动态能力没有增加反而减少。对于图9，期初动态能力的增加导致收益的增加，但收益增加的速度越来越慢，后期动态能力的过度增加，即对动态能力的过度投入会导致收益的降低。对于图10，投资的增长会带来收益的增加，当收益达到一定的顶点后继续投资不会带来收益的继续增加，此时收益开始下降，后期随着投资的继续增加，收益出现小幅度回升现象。这是因为期初在一定行业技术水平下，技术的投资收益率是有一个固定阈值的。在阈值到达之前，投资增加带来收益增加。当投资收益率达到现阶段本行业的固定阈值后，再继续投资不会导致收益增加，反而会因为投资过度带来收益的降低。后期随着行业所处外界环境的不断发展变化，前期投资带来企业技术、管理或其他方面的提高，使得企业投资收益率大幅度提升，逐渐弥补前期过度投资的亏损，导致收益出现回升现象。此时企业要把握市场先机，合理预估本行业现阶段技术水平投资收益率的最大固定阈值，最好把投资控制在收益到达顶点之前的投资范围内。

由时间序列图可以看出，动态能力、投资以及收益在短时间内波动很大，一定时间后基本趋于稳定，说明在此参数范围内，企业能较快处于稳定发展的状态。同理，固定其他参数不变，令初值x（t）=0.003，即初始值为[0.003，0.523，0.24]，此时系统的轨线再次发生了改变，如图12所示。

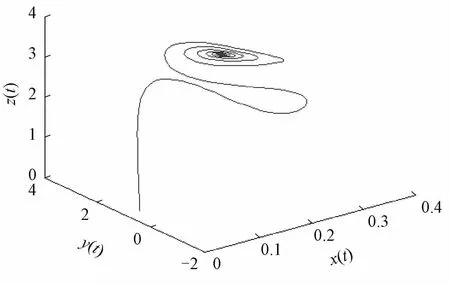
图12 改变初值后的投资收益吸引子

初值改变后所呈现的也是一个混沌吸引子，但可以明显地看到，该吸引子是与图2最初的投资收益吸引子，图7参数改变后的吸引子不同。上述分析说明，某一个参数或初始值的变化均有可能引起系统轨线的改变，系统对参数和初始值的变化有一定的敏感依赖性。

4 实证分析

4.1 参数获取

式（1）是根据企业动态能力、投资以及收益之间相互支持、相互制约的复杂关系建立的动态模型，其中参数的选取对实际有重要意义。本文根据统计公报、公司年报、相关网站及其他统计资料获得联想集团有限公司2004～2013年动态能力、投资以及收益的相关数据，运用非线性最小二乘回归法对参数进行拟合，得到实际系统中的参数。

本文参考联想集团有限公司信息披露文件中所涉及的内容，查阅相关文件及相关网站，经过多次比较筛选，最后制定了3项量化指标和14项非量化指标。本文的量化指标是研发费用、专利数量以及研发成果转化率，非量化指标如表1所示。在指标计算过程中，本文对每个量化指标赋予α的权重，对14个非量化指标赋予1-3α的权重。经调查，IT 企业的研发费用通常占总费用的15%～25%，且专利数量与研发费用密切相关，研发成果转化率也与研发费用及专利数量密切相关，本文取研发费用占总费用比值的平均值20%，以α=20%的情况进行分析[18]。

动态能力的评估结果来自于量化指标和非量化指标的整合，非量化指标的评估直接基于权重，因此可以直接将此部分数值结果与处理后的量化指标合并。在处理量化指标时，首先统计出每个指标序列的最大值（max）、最小值（min）和均值（mean），然后按照最大值为100、最小值为0、均值为50的标准将每个指标的数值进行转化。具体的公式为：

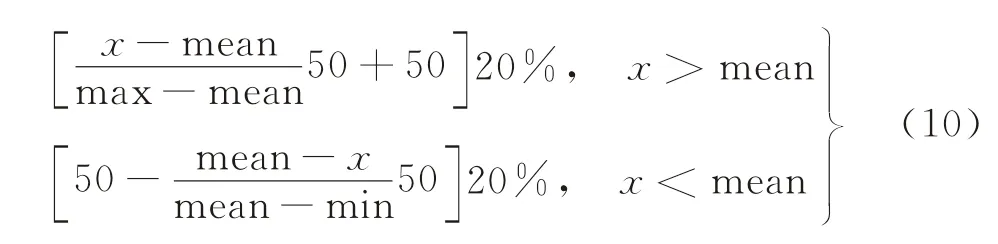
本文的投资为生产成本和销售、管理、财务费用以及研发费用的总和；收益为组织的税前利润。根据上述方法得到联想集团有限公司2004～2013年动态能力、投资和收益的相关数据如表2所示。

对表2中的数据进行归一化处理，用非线性最小二乘法拟合得到联想集团有限公司的相关系统参数如表3所示。

4.2 参数分析

4.2.1 动态能力、投资、收益的混沌现象分析 取系统参数为表3中的数据，任选一年的数据作为系统的初始值，本文选定2013年归一化后的数据作为系统的初始值，即初始值为[0.800 4 1 1]，可以得到联想集团有限公司实际系统的吸引子相图，如图13～16所示。由图13～16可以看出，实际系统的发展不是处于稳态发展的。系统的吸引子相图可以反映出在当前的各种条件下，系统动态能力、投资以及收益的发展轨迹和未来发展趋势，可以帮助组织更为有效地做出决策。

由图14可以看出，在一定时间内，动态能力增加，投资迅速增加，一段时间后随着动态能力的增加投资反而减少了。这是由于期初动态能力的提高使得企业的投资收益率会大幅度提高，所以企业大量投资，以便可以获得更丰厚的回报，但是此时的投资大多集中于设备、生产等，属于粗放式投资。后期随着动态能力达到一定程度时，行业领域倾向于以创新驱动、知识驱动等为企业带来收益，这时不需要大量的投资，企业依然能够获得可观的收益，所以后期随着动态能力的继续增大，投资会出现下降的趋势。对于图15，前一段时间中动态能力的增加促进了收益的增加，当收益增加到一个顶点后，对动态能力的过度投入会导致收益的减少；当收益减少到最低点后会出现反弹的现象，即收益会随着动态能力的增加继续升高，最后达到的最高值要比前一次达到的收益最高值要大。这可能是由于期初对动态能力的投入促进了动态能力的提高，进而使收益增加，当在一定范围内对动态能力过度投入时可能导致无效创新的出现或是科技成果转化率低下，这就给企业带来了一定的负担，导致收益的下降。后期随着企业经验的丰富和动态能力的提高，无效创新较之前有所减少，之前没有转化为生产的部分创新经过改进

表1 动态能力非量化指标评分标准[26-27]

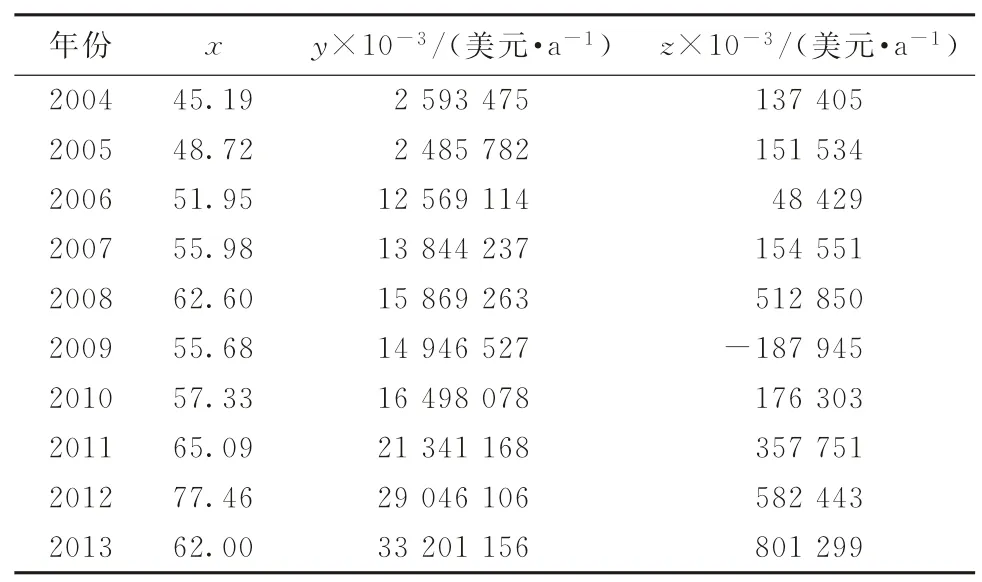
表2 联想集团有限公司动态能力、投资和收益的统计数据

表3 根据实际得出的式(1)的参数

开始转化为生产，带来了经济效益，使得企业的收益开始上升。图16说明，投资和收益出现了迂回的现象，期初投资和收益是近似线性的关系，投资增加带来收益增加；随着投资的继续增加，当收益达到一个顶点之后开始下降，但收益并非无限制的下降，后期收益又出现了迂回上升的情况，即投资减少收益反而增加，但此时收益的最高值较之前有所下降。这是由于期初投资增加导致收益增加，当投资收益率达到最大后再继续增大投资导致部分投资属于无效投资，增加的部分投资不能带来收益增加，反而给企业带来负担，使得收益减少。当收益减少到一定程度后，企业收回部分无效投资，减少资金占用，收益开始慢慢回升。实际系统的时间序列图如图17所示。

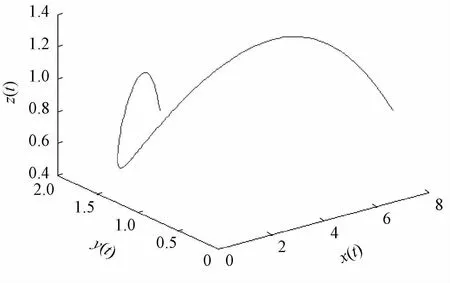
图13 实际系统关于x-y-z的三维图

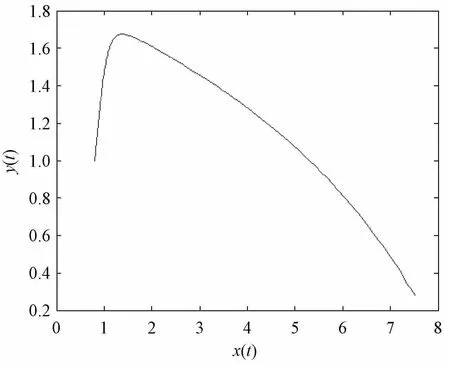
图14 实际系统关于x-y 的二维图

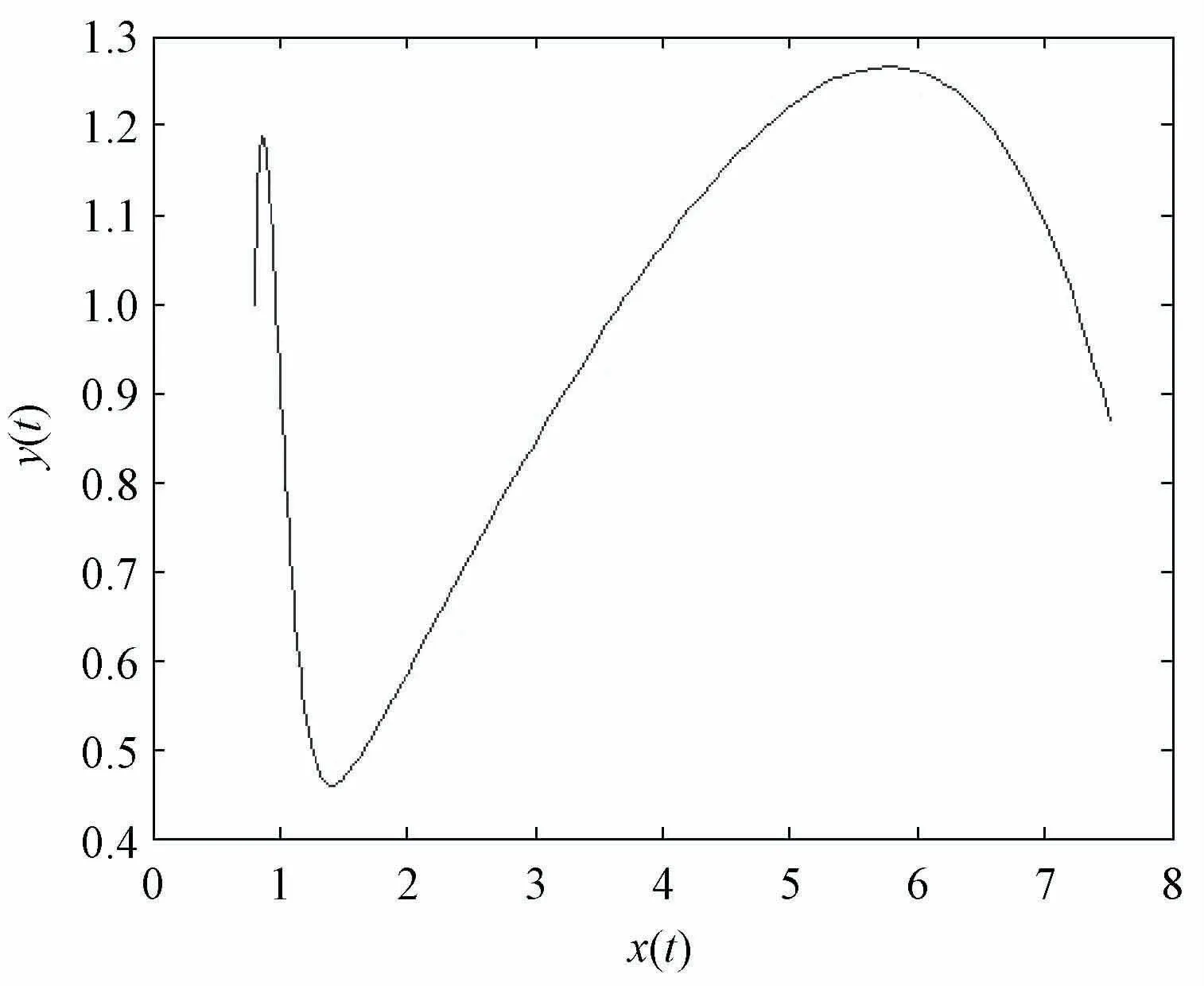
图15 实际系统关于x-z的二维图

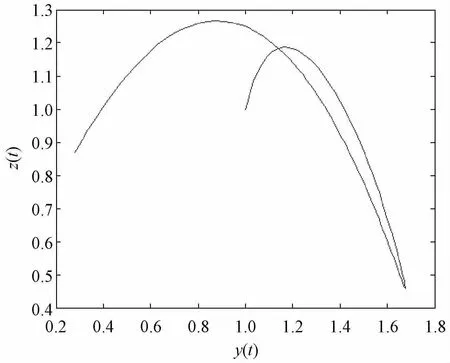
图16 实际系统关于y-z的二维图

图17 实际系统关于t-xyz的时间序列图

由图17可以看出，在此参数范围内，随着时间的增加，动态能力是增加的，并且增加的速率越来越快。在当前这种发展趋势下，随着时间的增加，投资在期初迅速增加，达到一个转折点后投资会随着时间逐渐降低。一段时间里收益随着时间的增加而增加，当收益达到一个最高点时，随着时间的增加收益会出现下降的现象。当收益降低到最低点时会出现回升现象，接下来收益越来越高，最后重新达到新的最高点，且此时的收益最高值比之前的最高值要略微高一些。这时需要组织及时地调整战略，促使组织朝着最有利于收益增加的方向发展。

4.2.2 系统对参数和初值的敏感依赖性混沌系统对参数和初始值有很强的敏感依赖性，其中一个参数或初始值的变化都有可能引起系统运行轨线的变化[17]。

取系统参数为表3 中的数据，初始值为[0.800 411]，把a1的值在原来的基础上增大0.5，即令a1=0.105 77，可得收益随时间变化的比较图，如图18所示。取系统参数为表3中的数据，初始值仍为[0.800 411]，把b2的值在原来的基础上分别减小0.1 和增大0.1，即b2=0.118 42，b2=0.318 42，可得收益随时间变化的比较图，如图19所示。取系统参数为表3中的数据，初始值为[0.800 411]，把y的值在原来的基础上分别减小0.1和增大0.1，即初始值分别为[0.800 40.91]和[0.800 41.11]，可得收益随时间变化的比较图，如图20所示。

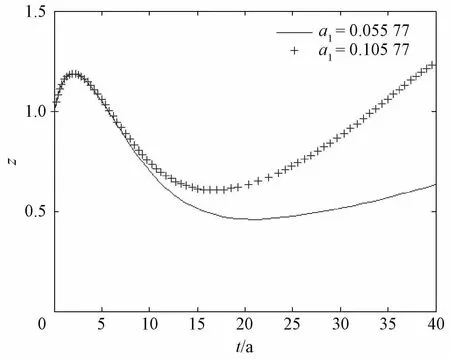
图18 改变a1后系统关于t-z的时间序列图

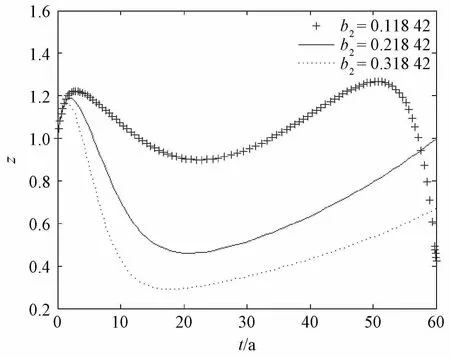
图19 改变b2后系统关于t-z的时间序列图

图20 改变y 后系统关于t-z的时间序列图

a1为动态能力的发展系数，对比观察图18两条曲线发现，在期初两条曲线是重合的，后期两条曲线开始逐渐分离，后期a1值较大的那条曲线较之前的曲线更高一点。这表明，单纯增大动态能力的发展系数，即增大动态能力的发展速度在短期内很难对收益增加产生作用，但是长期来看对企业收益增长是有利的。对于联想集团有限公司而言，目前制约收益增加的因素并不是动态能力不足，而是其他因素。因此，联想可以在短期内适当保持现在的动态能力水平。

b2为投资发展的弹性系数，b2的变化体现了投资发展的速度变化。图19显示了b2由小到大逐渐变化时收益变化的演化图。对比3条曲线可以看出，与b2=0.218 42的状况相比，当b2增大到0.318 42时，图形的峰值降低；当b2减小到0.118 42时，图形的峰值升高。说明在当前的状况下令投资发展速度的弹性系数变小，即投资发展变的略微缓慢时，在未来的时间中组织将会得到更大的收益。

当b2逐渐减小时，图形的波谷越来越高，且再次达到峰值的时间缩短。由图19中b2=0.118 42的曲线可以看出，图形的波谷比b2=0.218 42和b2=0.318 42时要略微高一些。说明略微减慢投资发展的速度可以减小收益波动的幅度，使组织发展趋向于稳定，且当收益再次升高时会达到比前期更高的收益水平。

y为组织的投资水平，y的大小体现了组织的投资力度。图20显示了y由小到大逐渐变化时收益变化的演化图。对比观察3条曲线发现，3条曲线的演化趋势非常一致，但是曲线在坐标中的高低位置不同。与y=1的情况相比，当y增大到1.1时，图形的最高点降低；当y减小到0.9 时，图形的最高点升高。表明投资力度在小范围内波动不会过于影响未来收益走势，但是会影响收益的高低水平。说明在当前的发展状况下，令投资y略微减少，在未来的时间中组织的收益将会更大。

在实际情况中，企业可以利用财务数据、咨询机构的定性数据，进行回归得到相关参数；同时，根据本企业上一年度的财务数据以及专业咨询机构的定性数据得到企业动态能力、投资以及收益的初始值。根据对上一年度的分析预测公司未来的动态能力以及投资的变化对收益的影响趋势；同时，参考国内外有关本行业的最大投资收益率对企业未来动态能力、投资水平进行决策。对于联想集团有限公司而言，目前状况下保持现在的动态能力，在一定范围内适当地降低部分固定资产投资，减少粗放式投资能够给企业带来收益；适当地减缓投资速度可以提高企业未来收益水平，促使企业健康发展。

5 结语

本文分析了企业动态能力、投资和收益之间的关系，运用非线性动力系统中的混沌分析理论，构建了三者之间的动态演化模型，基于一定的参数和初值分析了系统的混沌现象和系统对参数与初值的敏感依赖性。根据计算得出的实际系统中的参数和初值，讨论了参数和初始值变化对系统动态能力、投资和收益的影响，得到了影响收益增长的关键因素。

研究结果表明，动态能力对企业收益增加有促进作用，但是加快动态能力的发展速度并不能显著提高收益。动态能力对企业收益增加的促进作用是通过长期的、潜移默化的方式产生影响，企业需要适度提升自身的动态能力，但也要注意不能为了快速提升动态能力而忽视了投资、管理等其他因素对收益的影响；投资发展速度过快会造成企业收益波动幅度较大，不利于企业持续平稳发展；投资增加并不必然导致收益增加，投资水平要综合考虑现阶段的动态能力水平。企业在发展过程中要注意保持适度的投资发展速度，协调好动态能力与投资水平的关系会对企业未来发展有重要影响。

本文从动态能力、投资对企业收益影响的角度构建了企业动态能力、投资以及收益三者之间的三维非线性动态演化模型并进行探索式分析，在一定程度上可以为企业动态能力投入水平和投资决策提供借鉴。然而，在现实情况中，企业如何控制在主营业务上的投资及在其他附加业务上的投资比例也是影响企业获利的一个重要因素。进一步的研究将对企业的投资类别进行分类，分为基本业务型投资和知识创新型投资，考虑企业在其当前动态能力水平下如何控制基本业务型投资和知识创新型投资的比例问题。