关于高考中直接使用极坐标方程解题的一点思考

广东省珠海市斗门区第一中学(519000)李 凯 黎跃友

研究背景全国卷高考数学第22题考查的是选修4-4《极坐标与参数方程》的内容,对于不少问题,是直接用极坐标方程求解还是化成直角坐标方程求解,一直是学生很疑惑的事情,有时自己通过化成直角坐标方程后需要算很久才能得到答案,而参考答案中直接用极坐标方程很快就得到答案;可是有时直接用极坐标方程求解又出错或根本得不到答案,在一线教学中不少教师对极坐标系的讲解往往只强调会转化为直角坐标系中的问题来求解.广东步入全国卷已进入第三个年头,以前广东卷对4-4《极坐标与参数方程》的考查是一道填空题,而现在全国卷变为了一道解答题,以前基本会进行方程之间的互相转化即可应付考试,而现在在解答题中不仅考转化,而且还考查应用,在不少题目中直接用极坐标方程解题也许能简化计算,在教学中发现不少教师还是延续了备考以前广东卷的思想,没有挖掘极坐标知识的内涵,在教学中只强调让学生转化为直角坐标方程求解.

一、由一道考题学生作答情况引发思考

题目(2017年全国II卷第22题)在平面直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4．M为曲线C1上的动点,点P在线段OM上,且满足|OM|·|OP|=16,求点P的轨迹C2的直角坐标方程;(2)从略.

解法1(1)设P的极坐标为(ρ,θ)ρ＞0,M的极坐标为(ρ1,θ).由题设知|OP|=ρ,|OM|=由|OM|·|OP|=16,得C2的极坐标方程ρ=4cosθ(ρ＞0).因此,C2的直角坐标方程为(x-2)2+y2=4(x/=0).

解法2(1)设P的直角坐标为(x,y),曲线C1的直角坐标方程为x=4;可设M的坐标为(4,t),因为O,P,M三点共线,向量xt-4y=0,而P在线段OM上,显然P与原点不重合,故

而|OM|·|OP|=16,故

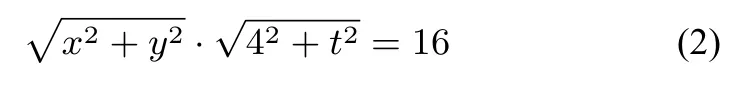
在某次模拟考试题中,我们把这道题选到试卷里作为检测题.解法1是原参考答案.发现大部分学生都用的是解法2的思路,把它当作解析几何里求轨迹来解决;而因为原本就惧怕解析几何中的计算,得到最终结果的很少,或者得到了最终答案的,也花费了很多时间,事实上本题直接用极坐标来解,即方法1,方便很多.

二、分析原因与寻找对策

高考考情分析笔者对比近三年的考试说明,发现有关对极坐标的考查说明几乎没有变化,在2018年的考试说明中对极坐标的考查主要有两点：(1)了解极坐标的基本概念,会在极坐标中用极坐标刻画点的位置,能进行极坐标和直角坐标的互化;(2)能在在极坐标系中给出简单图形表示的极坐标方程.从考试说明来看,一方面我们要会转化,我们也要会应用“简单图形表示的极坐标方程”.

学生学习误区由于在考题中碰到的极坐标方程都是我们熟悉的直线,圆,圆锥曲线,全部化为直角坐标方程当作一个解析几何问题是肯定能解出来的,不少学生以为全部转化为直角坐标方程解题就是解题的万能钥匙,事实上这把万能钥匙也只是应对了考试说明中“能进行极坐标和直角坐标互化”这一内容.

应对策略在高考题中碰到曲线的极坐标方程都是非常简单的,比如直线,极点为圆心的圆,经过极点的圆,还有圆锥曲线等都比较容易把曲线化为ρ=f(θ)或其它比较简单的形式.当求解一些可由点的极径表达的长度和用极径极角表达的面积问题时,直接用极坐标方程参与计算会方便很多.而转化为直角坐标方程还需联立方程和用到弦长公式以及点到直线的距离公式,计算量更大;另外还有一些与求曲线的轨迹方程有关的问题,比如几何特征比较明显或者一条曲线绕极点旋转得另一条曲线,直接寻找曲线上任意一点的极角与极径的关系式来求轨迹更容易.

三、分类剖析常见适用于直接用极坐标方程来解题的试题

类型1通过极径的运算来求弦长和面积.

例1(广西2017届联合检测)在直角坐标系xOy中,圆C的方程为以O为极点,x轴的非负半轴为极轴建立极坐标系.

解(1)2y-5=0,故其极坐标方程为0.(2)将得 ρ2-2ρ-5=0,由于 ρ1+ρ2=2,ρ1ρ2=-5,所以|MN|=|ρ1-ρ2|=

类型2通过极径来求一些与长度和面积有关的最值问题.

例2(2015年全国II卷第23题)在直角坐标系xOy中,曲线C1:(t为参数,t/=0),其中0≤α＜π,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sinθ,曲线C3:ρ=

(1)求C2与C3交点的直角坐标;(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.

解(1)联立曲线C2和C3的直角坐标方程,有解得C2与C3交点的直角坐标为(0,0)和

(2)曲线C1的极坐标方程为θ=α(ρ∈R,ρ/=0,其中0≤ α＜ π.因此A的极坐标为(2sinα,α),B的极坐标为时,|AB|取得最大值,最大值为4.

类型3几何特征比较明显或与绕极点的旋转有关的轨迹问题.

例3(石家庄市2017届第二次模拟考试)在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcosθ=a(a＞0),Q为l上一点,以OQ为边作等边三角形OPQ,且O,P,Q三点按逆时针方向排列.

(I)当点Q在l上运动时,求点P运动轨迹的直角坐标方程;(II)略.

解(I)设点P的坐标为(ρ,θ),则由题意可得点Q的坐标为再由点Q的横坐标等于a(a＞0),可得故当点Q在l上运动时点P的直角坐标方程为

类型4联立两个方程求交点极坐标或已知两个极坐标方程交点满足的条件求参数值.

例4(2013年全国I卷理科)已知曲线C1的参数方程为(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ-2sinθ.

(1)把C1的参数方程化为极坐标方程；

(2)求C1与C2交点的极坐标(ρ≥0,0≤θ＜2π).

解(1)C1的极坐标方程为ρ2-8ρcosθ-10ρsinθ+16=0.

(2)显然曲线C1不经过极点,即极点不是它们的交点,这样曲线C1和C2的交点的极坐标满足方程组

把C2的方程代入C1的方程,整理得16cos2θ-16sinθ cosθ=0,即16cosθ(cosθ-sinθ)=0,故cosθ=0或cosθ=sinθ,再结合0≤ θ＜2π,得 θ=分别代入C2的方程可得再结合条件ρ≥0,得C1与C2交点的极坐标分别为

例5(2016年全国I卷理科)在直角坐标系xOy中,曲线C1的参数方程为(t为参数,a＞0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cosθ.

(1)说明C1是哪种曲线,并将C1的方程化为极坐标方程；

(2)直线C3的极坐标方程为θ=a0,其中a0满足tana0=2,若曲线C1与C2的公共点都在C3上,求a.

解(1)消去参数t得到C1的普通方程x2+(y-1)2=a2.即C1是以(0,1)为圆心,a为半径的圆.将x=ρcosθ,y=ρsinθ代入C1的普通方程中,得到C1的极坐标方程为ρ2-2ρsinθ+1-a2=0.

(2)曲线C1与C2的公共点的极坐标满足方程组若ρ/=0,由方程组得16cos2θ-8sinθ cosθ+1-a2=0,由已知条件tanθ=2,可得16cos2θ-8sinθ cosθ=0,从而1-a2=0,解得a=-1(舍去),a=1.而a=1时,极点也为C1与C2的公共点,在C3上.所以a=1.

四、巩固练习

1(安徽省江淮十校2018届高联考理科试题)平面直角坐标系xOy中,曲线C1的参数方程为(θ为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为

(1)写出曲线C1的极坐标方程和曲线C2的直角坐标方程;

(2)若射线OM:θ=a0(ρ≥0)平分曲线C2,且与曲线C1交于点A,曲线C1上的点B满足求|AB|.

2(湖南省衡阳市2018届联考)在直角坐标系xOy中,曲线C的参数方程为(φ为参数).以坐标原点为极点,以x轴正半轴为极轴,建立极坐标系,A,B为曲线C上两点,且OA⊥OB,设射线OA:θ=a,其中

(1)求曲线C的极坐标方程;(2)求|OA|·|OB|的最小值.

3(张掖市民乐县第一中学2018届月考试题)在直角坐标系xOy中,已知圆C:(θ为参数),点P在直线l:x+y-4=0上,以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系．

(1)求圆C和直线l的极坐标方程;(2)射线OP交圆C于R,点Q在射线OP上,且满足|OP|2=|OR|·|OQ|,求Q点轨迹的极坐标方程．

解析与提示1.(1)C1:

五、2018年全国卷高考第22题回顾与分析

在刚刚结束的2018年高考中,全I卷(文理)第22题考查的是转化圆的极坐标方程为直角坐标方程后,已知直线与圆的交点个数,求参数的值;全国II卷和III卷(文理)均考的是参数方程的概念和应用.从全国三套卷来看,2018年并没有重点考查极坐标的应用.笔者认为这是一种考查知识点的正常轮换,因为在前三年(前面的例题可见)试题中有强调对极坐标知识的重点考查,今年对参数方程的考查更多一点,我们不能掉以轻心,不可弱化对这一知识的研究和教学.

六、教学建议与2019年高考展望

由于在高考试题中碰到的极坐标方程都是可以化成直角坐标方程的,以上所有的题目都可以转化成直角坐标方程来求解,当然如果都这样来处理,那么这道题就变成一个解析几何的附属品.而解析几何是高中阶段公认的难点,这对于学生来说是难以承受的.对于上面归纳的这些类型的题,在极坐标系下,学生只需运用三角函数运算即可解题,而三角属于高中阶段比较基本的知识,学生一般都较为熟练,这样解题就避免了很大的计算量,学生易于接受,这种解题方法与思想非常值得我们教学中教给学生.而且从知识的完备性和后续知识的学习的角度来看,学生理解极坐标系下解决某些问题的优越性是非常有必要的,比如螺旋线(注：不在高考考察范围内)的方程为ρ=θ,转化为直角坐标方程后形式较为复杂,也就是说极坐标系有助于拓展我们认识曲线的功能.

除了研究教材和高考真题外,每年的考试说明中的题型示例以及参考答案也能指导我们教学和备考.在2018年版的考试说明中有关22题的题型示例共两道,其中一道的参考答案就是直接用极坐标方程来解题的,现摘录如下：

2018年版考试说明中的选考内容题型示例2在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25.

(1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程;(2)直线l的参数方程是(t为参数),l与C交于A,B两点,|AB|=10,求l的斜率．

解(1)由x=ρcosθ,y=ρsinθ,可得圆C的极坐标方程为 ρ2+12ρcosθ+11=0.

(2)在(1)中建立的极坐标系中,直线l的极坐标方程为θ=α,(ρ∈R).设A,B所对应的极径分别为ρ1,ρ2,将l的极坐标方程代入圆C的极坐标方程得ρ2+12ρcosθ+11=0,于是ρ1+ρ2=-12cosθ,ρ1ρ2=11,所以|AB|=|ρ1-ρ2|=

2018年高考中侧重考查的是参数方程,展望2019年,我们要对这一命题方向要更加重视.从2016年高考开始,全国大部分地方都并入了全国卷,在以前各省命题时,有关极坐标的考查多数是只考一道填空题,而现在全国卷对这一知识的考察是一道解答题,知识的深度广度都有增强.因此,需要我们对知识进行深层次的挖掘.