设点法设线法探讨一道解析几何题的解法
湖北省阳新县高级中学(435200)邹生书
山西省长治市沁县中学(046400)王 河
解析几何就是用代数方法解决几何问题,在高中阶段就是用方程思想来处理直线与圆锥曲线及其位置关系等问题.在高考中圆锥曲线必考一道大题,主要考查直线方程及圆锥曲线的标准方程、离心率等几何性质,考查定值定点、最值和取值范围等问题,重点考查运算求解能力.圆锥曲线大题往往是题设条件多、关系错综复杂的动态问题,大多考生对这类问题常常不知从何下手,不知道是该设点的坐标还是设直线方程?怎么设?设多少个未知数?怎么列方程?怎么求解等?对考生的运算求解能力是一个很大的挑战.解答这类问题需要考生既能冲锋限阵斩将夺关,又能统领三军,运筹帷幄之中,决胜千里之外.下面以一道圆锥曲线问题的解法为例,说明如何用设点法和设线法解决直线与圆锥曲线的有关问题,与读者交流.
题目如图1,已知椭圆O:点B,C分别是椭圆O的上下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.
(1)已知直线BM,BP的斜率分别为k1,k2,求证:k1k2为定值;
思路一通过设点的坐标切入求解.
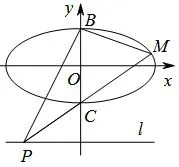
图1
解法1(1)设点P(x0,-2),M(x,y),则将其代入椭圆方程整理得
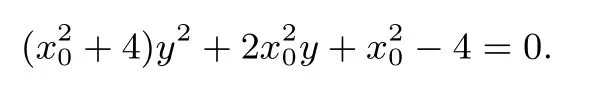
因为直线PC与椭圆相交点C,M,则点C,M的纵坐标是这个方程的两个根,而点C的纵坐标为-1,由根与系数关系两根之积求得点M的纵坐标为代入x=-x0(y+1)得点M的横坐标为于是
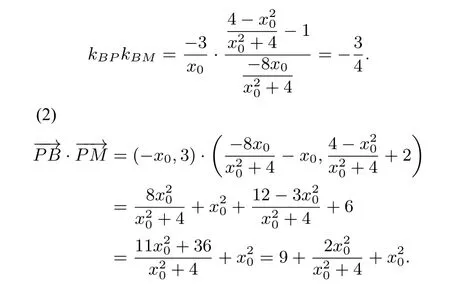
因点M与点B不重合,故x0/=0,则所以的取值范围是(9,+∞).
解法2(1)设点P(x0,-2),因为点M在椭圆上,由椭圆参数方程设M(2cosθ,sinθ),则

点评上述两种方法通过设动点P,M的坐标切入求解,其中解法2用椭圆的参数方程设点M的坐标,然后根据P,C,M三点共线用向量共线的坐标运算列方程求解.解法1是将点P作为主动点,用点P的横坐标x0表示从动点M的坐标以及斜率k1,k2,解法2是将点M作为主动点,用参数角θ表示点P的横坐标及斜率k1,k2.第2问都采用分离常数法求取值范围.
思路二通过设直线的方程切入求解.
解法3(1)因为直线PM过点C(0,-1),故可设直线PM的方程为y=kx-1,将其代入椭圆方程整理得(4k2+1)x2-8kx=0,此方程的两个根分别是直线PC与椭圆交点C,M的横坐标,而点C的横坐标为0,则点M的横坐标为代入y=kx-1得点M的纵坐标为则直线BM的斜率
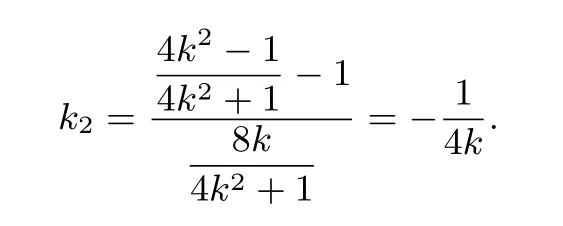
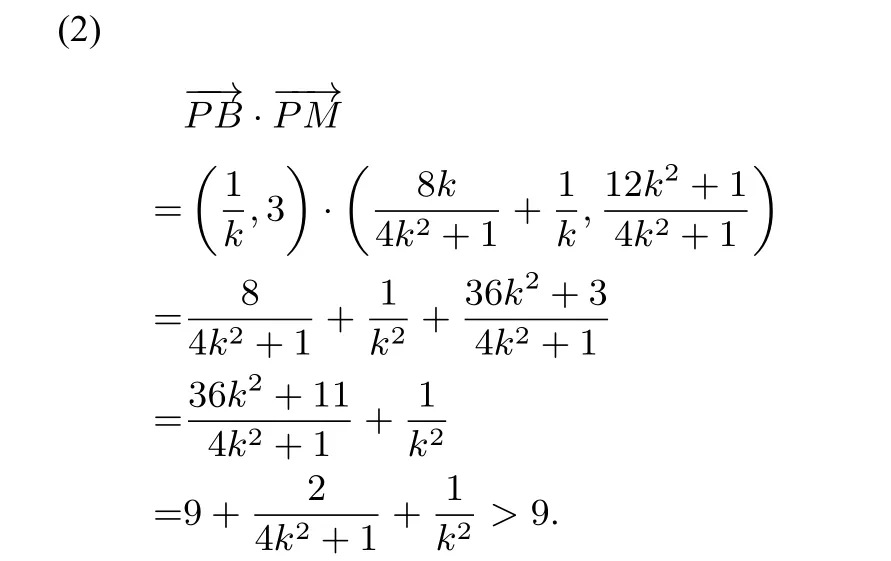
解法4(1)因为直线PM过点C(0,-1),故可设直线PM的方程为y=kx-1.因为BC为椭圆直径,由文[1]知在y=kx-1中令y=-2得点P的横坐标为则直线BP的斜率所以
(2)同法3略.
点评解法3和解法4均以直线PM的点斜式方程切入求解,用直线PM的斜率k表示点P,M的坐标及斜率k1,k2,其中解法4运用椭圆直径斜率的性质求解,在证明k1k2为定值时可以起到简化运算缩小解题长度的作用.
解法5(1)因为直线BP过点B(0,1)且斜率为k1,故直线BP的方程为y=k1x+1,令y=-2得点P的横坐标为因为BC为椭圆直径,由文[1]知所以
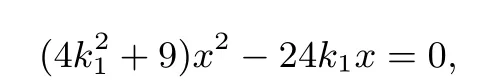

解法6(1)因为直线BM过点B(0,1)且斜率为k2,故直线BM的方程为y=k2x+1.因为BC是椭圆直径,由文[1]知所以直线PC的方程为令y=-2得xP=4k2.又直线PB的方程为y=k1x+1,令y=-2得于是有
(2)将直线BM的方程y=k2x+1代入椭圆方程整理得

因为直线BM不平行于x轴,所以k2/=0,故的取值范围是(9,+∞).
点评解法5(解法6)以直线BP(BM)的点斜式方程切入求解,用其斜率k1(k2)表示点P,M的坐标及另两条直线的斜率,这两种解法充分运用题目所设斜率k1,k2,不再另外设点的坐标或设直线PM的方程,虽然解法与法3法4整体上大同小异,但解法直接.
笔者在文[1]中介绍了椭圆直径三角形斜率的一个性质与应用,性质如下:
性质已知AB是椭圆或圆C:0)的任一直径,点P是曲线C上异于A,B的任意一点,若直线PA,PB都不平行于坐标轴,则
当椭圆试题中涉及直径三角形斜率的有关问题时,宜用直线点斜式方程的设线法,若能运用上述性质处理则解法更加快速高效.
高考链接2009年高考福建卷理科第19题第2问题,2011年高考江苏卷理科第18题第3问,2012年高考湖北卷理科第21题第2问等,可用设线法结合性质求解,考题如下,解法见文[1]这里从略.
1(2009年高考福建卷理科第19题)已知A,B分别为曲线C:=1(y≥0,a>0)与x轴的左右两个交点,直线l过点B,且与x轴垂直,S为l上异于点B的一点,连结AS交曲线C于点T.
(1)若曲线C为半圆,点T为圆弧AB的三等分点,试求出点S的坐标;
(2)点M是以SB为直径的圆与线段TB的交点,试问:是否存在a,使得O,M,S三点共线?若存在,求出a的值;若不存在,请说明理由.
2(2011年高考江苏卷理科第18题)如图2,在平面直角坐标系xOy中,M,N分别是椭圆=1的顶点,过坐标原点的直线交椭圆于P,A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C.连接AC并延长交椭圆于点B,设直线PA的斜率为k.
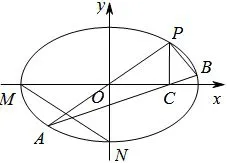
图2
(1)当直线PA平分线段MN时,求k的值;
(2)当k=2时,求点P到直线AB的距离d;
(3)对任意的k>0,求证:PA⊥PB.
3(2012年高考湖北卷理科第21题)已知A是单位圆x2+y2=1上的任意一点,l是过A点与x轴垂直的直线,D是直线l与x轴的交点,点M在直线l上,且满足|DM|=m|DA|(m>0且m/=1),当点A在圆上运动时,记点M的轨迹为曲线C.
(1)求曲线C的方程,判断曲线C为何种圆锥曲线,并求焦点坐标;
(2)过原点且斜率为k的直线交曲线C于两点P,Q,其中P在第一象限,它在y轴上的射影为点N,直线QN交曲线C于另一点H.是否存在m,使得对任意的k>0,都有PQ⊥PH?若存在,求m的值;若不存在,请说明理由.
解析几何就是用代数的方法解决几何问题,设点法和设线法是解决动直线与圆锥曲线相交问题的基本方法.当三点共线时用向量共线的坐标运算求解可避免对直线斜率存在性的讨论,中点弦问题的点差法是设点法的经典解法.直线方程与圆锥曲线方程联立组成方程组,用方程思想和一元二次方程根与系数关系求解是解决这类问题的通性通法.在解题过程中要有目标意识,在用设点法或设线法求解时,要注意“主”与“辅”的关系,要始终围绕目标和解题计划展开求解,抓住问题的主要矛盾,抓住矛盾的主要方面,抓住牛鼻子牛就怪怪地跟着你走了.在设点或设线法中,若能用某个点的坐标或某直线方程中的某一个或几个变量去表示其余的点的坐标或直线的方程,这样抓住“牛鼻子”就使得定值证明、最值求解和取值范围问题迎刃而解了.

