一道高三诊断题引发的推广*

甘肃兰州第五中学(730000)李守明

甘肃兰州第五十二中学(730000)司 恺

题目(兰州市2017年高考诊断考试理科第20题)已知椭圆C:=1(a＞b＞0)经过点且离心率为

(1)求椭圆的方程;

(2)设M,N是椭圆C上的点,直线OM与ON(O为坐标原点)的斜率之积为若动点P满足试探究：是否存在两个定点F1,F2,使得|PF1|+|PF2|为定值?若存在,求F1,F2的坐标;若不存在,请说明理由.

1 试题来源及解答

该试题实际上是对重庆2011年高考理科20题的简单改变,原试题的题设条件为：椭圆的中心为原点O,离心率一条准线的方程为原试题的问法和本次诊断考试试题的问法完全相同.作为高考试题,凝聚着命题者的智慧,对高中数学教学起着积极的导向作用,是教学研究的重要内容,也成为各级考试争相模仿和改编的素材,若我们能对高考试题进行探究,剖析高考试题的本质,加深对问题的理解,则会收获意想不到的惊喜!下面给出本试题的解答：

解(1)

(2)设P(x,y),M(x1,y1),N(x2,y2),依题意kOM·即x1x2+2y1y2=0,则由

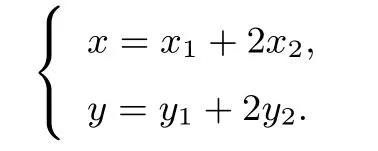
2 试题的推广

推广1设M,N是椭圆C:=1(a＞b＞0)上的点,直线OM与ON(O为坐标原点)的斜率之积为若动点P满足则点P的轨迹方程为

证明设P(x,y),M(x1,y1),N(x2,y2),依题意kOM·又由

推广2设M,N是双曲线C:=1上的点,直线OM与ON(O为坐标原点)的斜率之积为若动点P满足则点P的轨迹方程为

证明设P(x,y),M(x1,y1),N(x2,y2),依题意kOM·又由

推广3设M,N是椭圆C:上的点,直线OM与ON(O为坐标原点)的斜率之积为若动点P满足则点P的轨迹方程为

证明设P(x,y),M(x1,y1),N(x2,y2),依题意kOM·又由

故

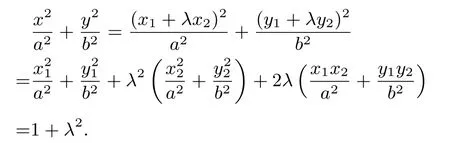
推广4设M,N是双曲线C:=1上的点,直线OM与ON(O为坐标原点)的斜率之积为若动点P满足则点P的轨迹方程为C:

证明设P(x,y),M(x1,y1),N(x2,y2),依题意kOM·又由

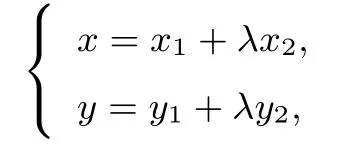
故

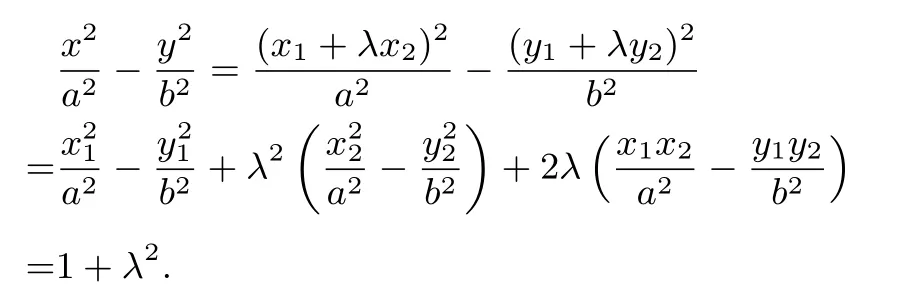
推广5设M,N是椭圆C:上的点,直线OM与ON(O为坐标原点)的斜率之积为若动点P满足则点P的轨迹方程为C:

证明设P(x,y),M(x1,y1),N(x2,y2),依题意kOM·又由

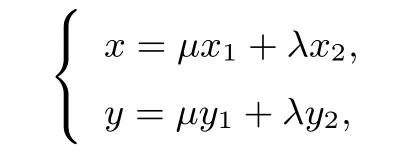
故

显然是椭圆.

推广6设M,N是双曲线C:上的点,直线OM与ON(O为坐标原点)的斜率之积为若动点P满足则点P的轨迹方程为C:

证明设P(x,y),M(x1,y1),N(x2,y2),依题意kOM·又由

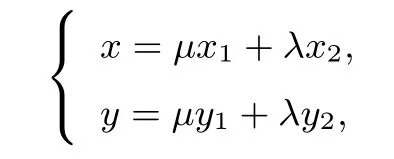
故

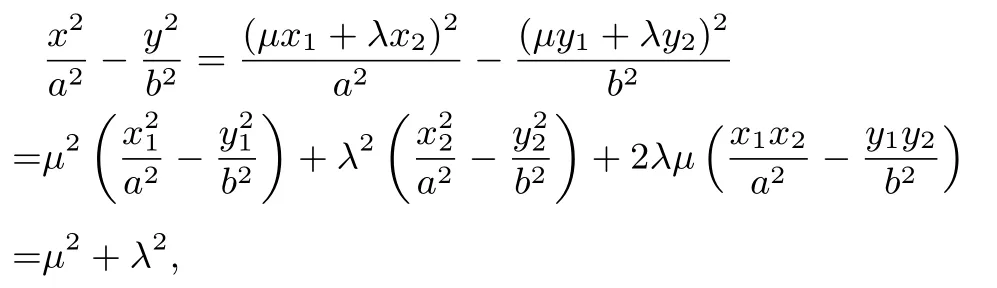
显然是双曲线.