关于三角函数图像的选择填空题的简便解法
广东省佛山市顺德区容山中学(528303)李洪波
高中三角函数部分的考察很多都是先求解析式,只要把解析式化成f(x)=Asin(ωx+φ)的形式,后面的解答过程都有固定的套路.解析式中A,ω,φ也有固定的方法求解,但常规解法有时会比较繁琐易错.本文从“五点法”作图的知识入手,通过“关键点”,充分挖掘正弦型三角函数的特点,将其性质在图像中显示出来,以图促思,简化过程,从而快速找到解决问题的方法.
类型一:利用“五点法”拓展图形
例1函数f(x)=的部分图像如图1所示,则f(x)的单调递增区间为___.
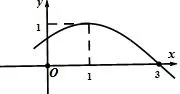
图1

图2
解析此题的常规解法是先根据图像求出解析式,再求单调区间.由于此题较为简单,而且图形的信息点足够,很多学生浅尝辄止,没进一步的思考,深究图形的特点.其实我们可以利用“五点法”把图形进行拓展,如图2,由图可知[-3,1]为其一个单调递增区间,再观察出函数的周期为8,所以其单调区间为[-3+8k,1+8k],k∈Z,这样过程就简化了很多.
例2(2016新课标1理科)已知函数f(x)=sin(ωx+φ)(ω >0,|φ|为y=f(x)图像的对称轴,且f(x)在单调,则ω的最大值为()
A.11B.9C.7D.5
解析根据零点与对称轴是可以把函数图像作出来的,有了图像直接看其在是否单调即可.如图3,对称轴可能在图中1,2,3,4...等位置,一一验证即可.当在1的位置时,则ω=1,显然函数在上单调;当在2的位置时,则ω=3,且区间夹在相邻两条对称轴之间,所以单调;(具体数据的标识如图4)可以知道,后面ω的值依次为5,7,9,11...,结合答案选项,再验证一下11与9,发现答案是9.这里不需要把每个值都算出来,只需求出对称轴即可.图5为ω=11时的函数图像,由则从开始往左边数,每次递减即可求出各个对称轴的坐标,此时就会发现对称轴恰好在区间(内,故在此区间函数不单调.
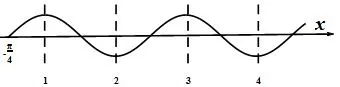
图3
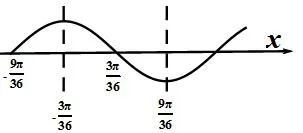
图4

图5
有很多解法是先把φ的值算出来(具体算法在这里就不赘述了),0,那么会不会与上面的图像相矛盾呢?注意到图中的图像都是从往右向上走的,如果它与y轴交于下方,则可以让图像从往右向下走的,对单调性是没有影响的.
类型二:锁定关键点,利用图像的平移知识解决问题
例3函数f(x)=Asin(ωx+φ)的部分图像如图6所示,则其解析式为___.
解析解析式中的A与ω容易求得,φ的求法一般是代点求值,由于此题没有给定φ的范围,所以在解答过程中会面临取舍困难.由图易知,A=2,T=π,所以ω=2,y=2sin(2x+φ).观察到图中的点A横坐标为所以函数图像是由y=2sin2x向右平移得到的,所以

图6
例4将函数y=-cos2x的图像向右平移m(m>0)个单位以后图像与y=sin2x关于对称,则m的最小值为___.
解析因为对称是相互的,所以我们可以先求出y=sin2x关于对称的函数,则这个函数是由y=-cos2x向右平移m(m>0)个单位得到的,这样就可以避免带参数的运算.当然,求解y=sin2x关于对称的函数解析式,计算量也不小,这时我们可以锁定关键点,进行平移,从而避开这个运算.y=sin2x的一个最高点为它关于对称的点为而y=-cos2x上的在的左边且与距离最小的最低点为(0,-1),所以m的最小值为
三角函数的平移对称一定要锁定“关键点”,直接看这个点是怎样变化的就行了.一般情况下如果能准确判断出第一零点的位置,则选用第一零点最为方便,如果不能,也可选用最高(低)点.
类型三:充分利用函数图像的对称性
例5已知函数f(x)=Acos(ωx+φ)的图像如图7所示,
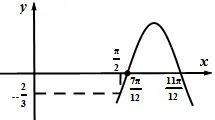
图7
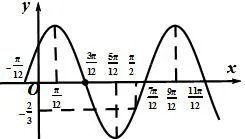
图8
解析此题的常规解法就不赘述了.根据正弦型函数的图像性质我们可以把题目中的图形加以拓展,如图8,我们会发现距离0最近的对称轴为最近的对称轴为它们与最近对称轴之间的距离都是一个在x轴上面,一个在x轴下面,所以它们的值互为相反数,故
我们发现,正弦型三角函数图像上距离最近对称轴(或对称中心)距离相等的点,它们的值相等或互为相反数.
例6已知函数其中x∈[(其中m∈R,且若f(x)的值域是则m的取值范围是___.
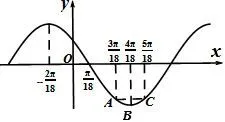
图9
解析此题我们先求出一个最高点的坐标,如由于周期几个关键点的横坐标成等差数列,于是快速作出图像如图9,在这里作图时最好从最高点或最低点开始,这样就会清楚地知道曲线的下一步走向.一般情况下,正弦型三角函数图像可以先画出一条波浪线与x轴,然后从一个最高(低)点出发,每次递增来描出关键点.经计算可知=-1,所以m的取值就介于B,C两点之间,且A,C关于对称,所以C的横坐标为
充分利用图形的对称性,可以减少很多计算量.
类型四:利用伸缩变换的比例求值
解析由于周期个单位比还小,所以可得到函数图像如图10,由图可以知道则所以f(0)的值与的值相同,故

图10

图11
这里参照了特殊角的三角函数值,正弦型三角函数f(x)=sin(ωx+φ)均可看作是由正弦曲线y=sinx通过一系列变换得到,我们发现,在变换过程中,如果|OB|:|OA|的值不变,则函数在点B处的函数值也不会变.如图11,如果则点B处的函数值就与相同,如果则函数在点A处的函数值就与互为相反数,这里的正负可以直接从图形上看出来.
另外,如果振幅A有变化,则只需要在值前面乘以A即可.
正弦型三角函数进行伸缩变换时,伸长缩小的比例都是一样的,弄清楚这个变化,就可以类比y=sinx来求值.在解题过程中我们充分利用这个特点,就会有意想不到的收获.

