对两类周期数列的研究

辽宁省黑山县第一高级中学数学组(121400)刘大鹏 王洪峰

各种竞赛中经常出现周期数列,这引起了笔者的兴趣,经过认真研究,有些收获.现整理成文,供同行参考.

一、类型I数列的通项

我们称形如：已知a1,a2,an+2=aan+1+ban,(a2+4b＜0)的数列为类型I数列.以下讨论该型数列通项公式的求法.

定义方程x2-ax-b=0叫做递推公式an+2=aan+1+ban的特征方程,其根叫做特征根.

定理1若特征方程有两个共轭虚根x1=r(cosθ+isinθ),x2=r(cosθ-isinθ),则

其中c1,c2是

的唯一解.[1]

证明(用第二数学归纳法)

i)当n=1时,a1=r(c1cosθ+c2sinθ),结论成立.

ii)将特征根带入特征方程,得

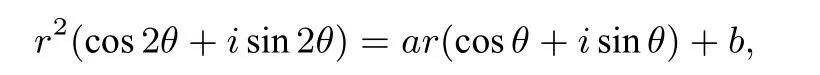
所以

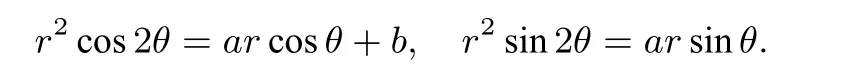
假设an=rn(c1cosnθ+c2sinnθ)对不超过k(1＜n≤k)的自然数成立,当n=k+1时,

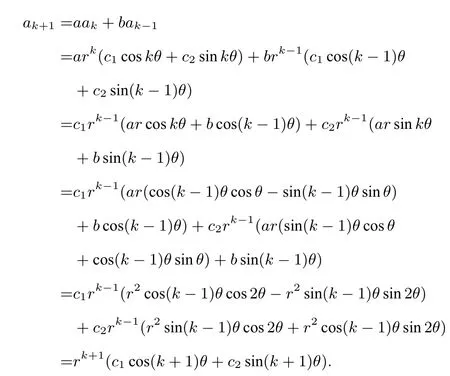
综上,结论对一切自然数n都成立.

推论1在定理1中,若r=1,k＞1,k∈N,则{an}是周期为k的数列.

推论2在推论1的条件下,{an}的相邻k项的和为0.

证明证法一：结论等价于Sk=0,cosθ+cos2θ+同理sinθ+sin2θ+···+sinkθ=0.

证法二：见文[5]中引理1的证明.

二、类型II数列的通项

我们称形如：已知a1,an+1=f(an),a1/=f(a1)的数列为类型II数列,其中(c/=0,ad-bc/=0).

定义方程f(x)=x的根叫做函数f(x)的不动点.

定理2当函数f(x)有两个相异的不动点p,q时,{是等比数列;当函数f(x)有唯一的不动点p时,是等差数列.[2]

推论3在定理2中,p,q是共轭复数时,记

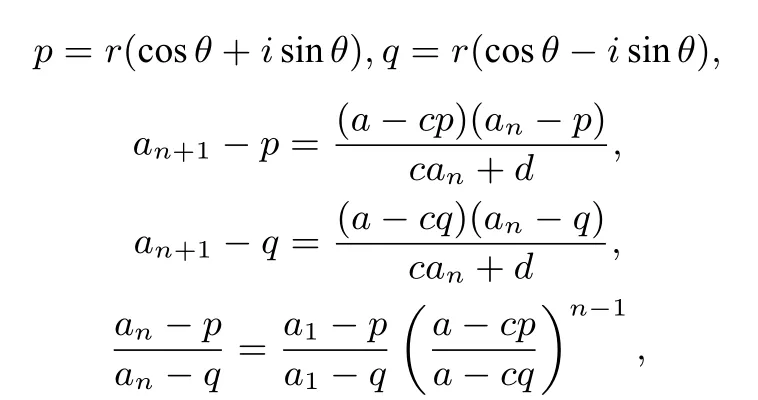
三、考题再现

例1(1989年浙江高中数学竞赛)数列{an},an+1=求a1001-a401的值.

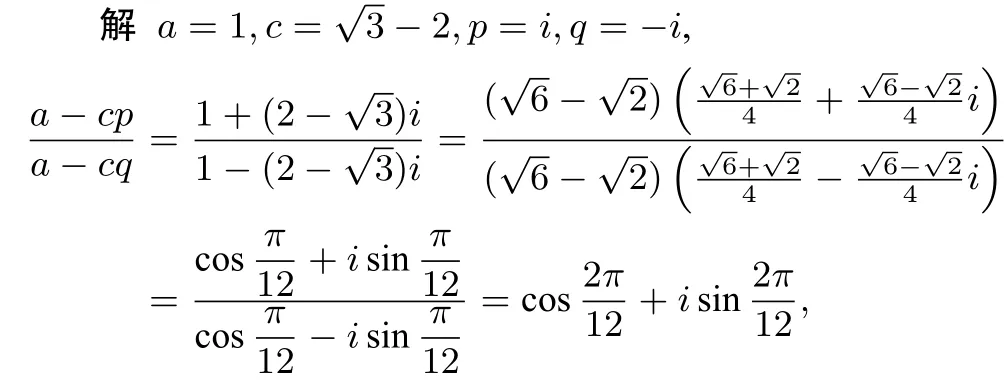
所以T=12,600=12×50,所以a1001-a401=0.

例2(2005湖南高考题)已知数列{an},a1=0,求a20的值().

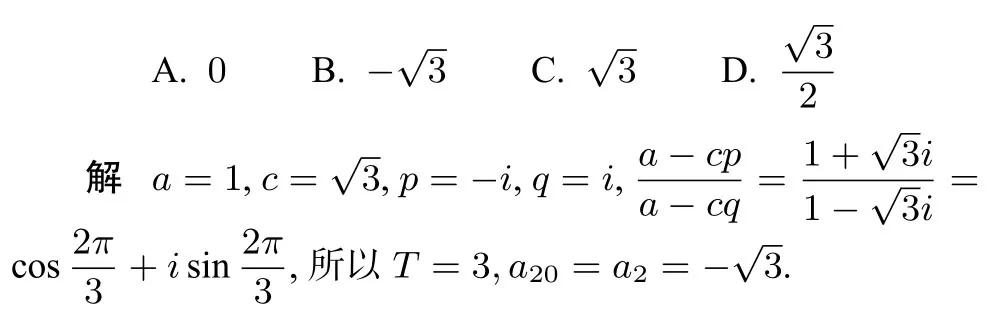
例3(1985年美国数学邀请赛试题)已知整数数列{an}满足an+2=an+1-an,S1492=1985,S1985=1492,求S2001的值.[3]

解特征根所以T=6,an+3=an+2-an+1=-an,由推论2,S1492=S6×248+4=a1+a2+a3+a4=a2+a3,S1985=S6×330+5=S5=-a6=a3=1492,a2=S1492-S1985=1985-1492=493,a1=-a4=a2-a3=493-1492=-999,S2001=S6×333+3=S3=986.

以下两题供读者练习：

1.(2006山西预赛试题)已知数列{an},an+2=an+1-an,a2=1,S2005=2006,求S2006的值.[4]

2.(1994年第5届希望杯题)已知数列{an},a1=13,a2=56,an+1=an+2+an,求a1994的值.

答案1.S2006=2007;2.a1994=56.

鸣谢对张兴波校长提供的帮助表示衷心的感谢!