变量有误差的半参数模型的经验似然推断
刘 彭,张 超,柳平增
(山东农业大学a.应用统计与农业信息化实验室;b.大数据中心,山东 泰安 271000)
0 引言
经验似然方法是Owen[1]在1988年提出的一种非参数统计推断方法,这种方法具有很多优点:可以完全根据数据来决定变量对应的置信区间,便于将多元数据进行组合,还可以合并偏度信息,使得删失数据或缺失数据的样本更易于处理,具有纠偏性、无需构造统计量等。因此,经验似然方法在半参数回归模型的各个领域应用广泛。
半参数回归模型既含有参数分量,又含有非参数分量,结合了线性回归模型和非参数回归模型的优点,因此不论是在理论研究上,还是在实际应用中都具有重要意义。经验似然方法已大量应用于半参数回归模型中,本文考虑变系数部分线性模型:

对于模型(1)的经验似然推断已有了大量的研究,如Hu[2]在2009年对变量有误差的变系数部分线性模型进行了研究,在两种不同的情况下,提出了参数部分经验对数似然比,构造了参数部分的置信区间,Huang[3]在2009年对模型(1)利用经验对数似然方法构造了非参数部分的置信区间,同时得到了估计的经验似然比服从标准卡方分布。本文针对变量有测量误差的变系数部分线性模型,提出了非参数部分的经验似然,并用对数似然法构造了非参数部分的置信区间,证明了估计的经验似然比服从标准卡方分布:

其中Eη=0,Eη2=Ση,且η与( )X,Z,U,ε独立。
1 估计的经验似然
为了定义经验似然估计量,先假设β已知,可以利用约束,其中f(u)为U的密度函数,并有一个紧支撑S(f)。由此,引入如下辅助随机向量:

其中h是带宽,Kh(·)=h-1K(·h)且K(·)是核函数。
如果β已知,由于是独立的且,则可以构造估计方程,此方程的解为α(u)的最小二乘估计,同样可以通过经验似然方法得到,因此,下面定义剖面经验对数似然比函数:
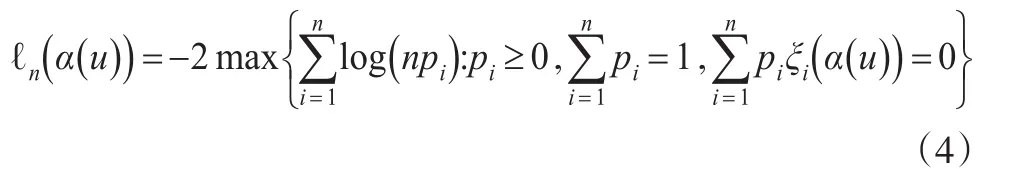
若α(u)为真参数,则 ℓn(α(u) )服从自由度为p的标准χ2分布,但是这里β未知,要对 ℓn(α(u) )进行分析,比较可行的方法就是用估计量β̂来代替β,下面就来估计β:
对l=1,…,p用kl个基函数的线性组合来逼近变系数函数为kl×1基函数向量,为kl×1未知函数向量,此方法的优点在于:kl可任意增大,从而存在的线性组合很好地逼近任何光滑函数αl(U),故其逼近的均方误差可任意小。
定义K×1阶矩阵逼近,此时,式(2)等价于:

令:

又式(2)可以写成矩阵形式:


下面用修正的最小二乘法估计:

即得到估计量:
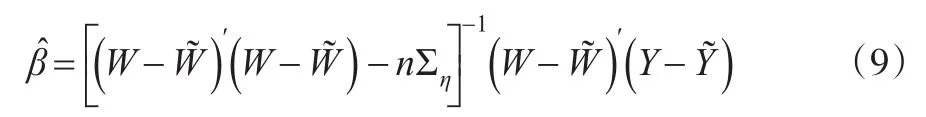


其中λ满足:

若α(u)为真参数,则分布,要得到这个结论,下面先给出一个定义和一些条件:
定义1:Ç是一个函数类,如果Ç中任一函数g(x,z)满足:
上述定义的详细介绍参考文献[4]。
条件1:u的密度函数f(u)有紧支撑S(f),对所有l,k=1,…,p,γl,k(u),f(u)在u0处有连续一阶导,对每个r=1,…,p,αr(u)在u0处的二阶导数为连续有界函数;
条件2:核函数K(u)为有界对称密度函数,其导数有界,且满足
条件 3:存在τ>1,使得
条件6:①对每个K,存在非奇异阵B,使得的最小特征值在K上一致有界大于 0;②存在满足和K=Kn的序列ζ0(K),使得,其中S是(x1,u1)的支集。
定理1:在条件1至条件7下,且满足h→0,nh3→∞,nh8→0, 若α(u0)为 真 参 数 ,那 么
根据定理1,α(u0)的置信区间可以由式(10)构造,对任意的的置信区间。
2 部分剖面经验似然比
为了构造α(u)的分片置信区间,这里借助部分剖面经验似然方法来定义αr(u)的经验对数似然比函数:考虑估计方程,这里er是第r个元素为1,其余元素为0的p维向量,α̂(·)为的最小值,这里假设Q(u)可逆,对任意的h,联合式(11)得:
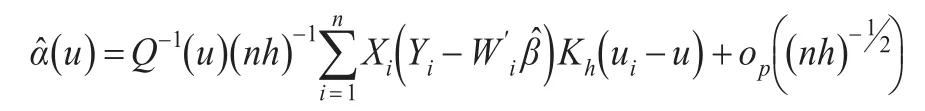
其中,α̂(u)等价于最小二乘估计,具体参考文献[5]。
对数似然比函数为:

从定理2可将αr(u0)的置信区间定义为:

3 主要结果的证明
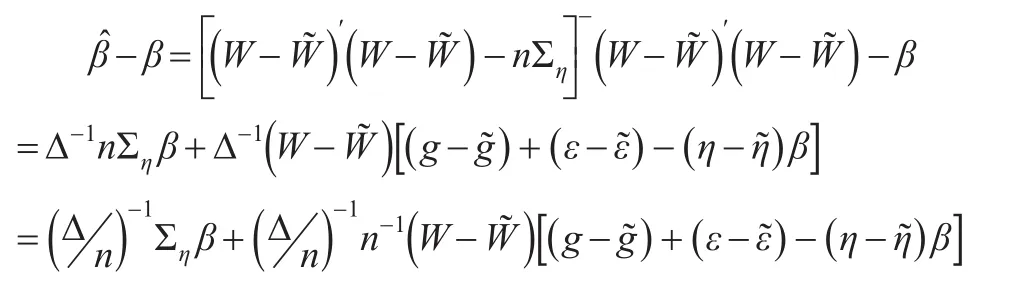

根据大数定律有:



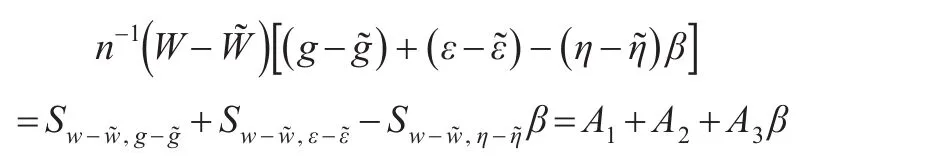
下面逐项证明:
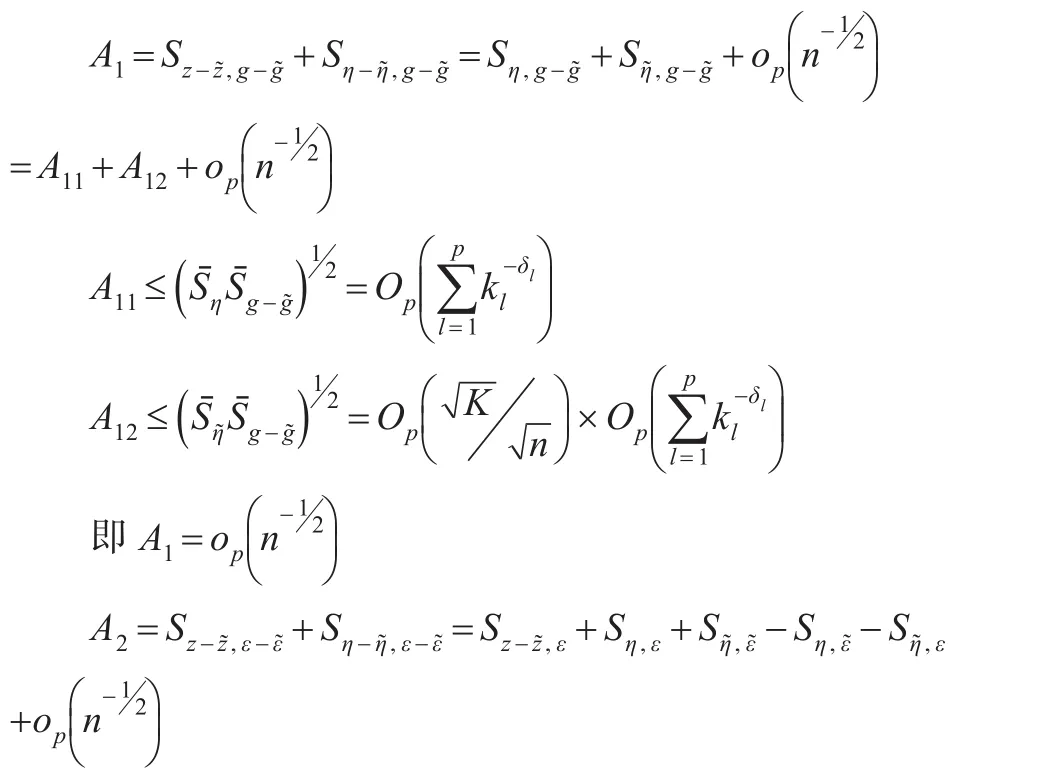
其中:
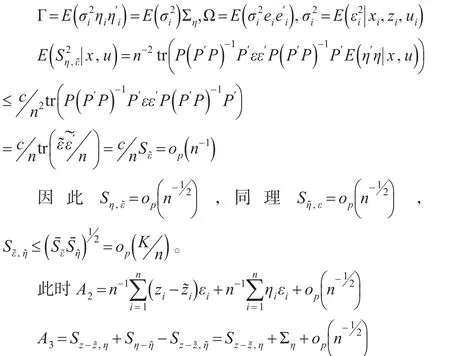

显然结论得证。
引理2:在定理1的条件下,如果α(u0)是真参数,则有

这里仅证A4,A5,其他的类似可以得到。
对任意的δ>0,

故A4=op(nh)12,A5=op(nh)12,即结论成立。
引理3:在定理1的条件下,如果α(u0)是真参数,那么:
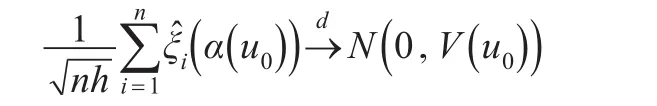
引理4:在定理1的条件下,如果α(u0)是真参数,那么:
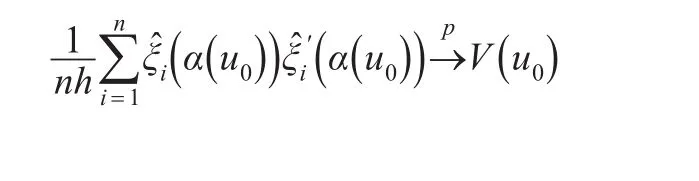
引理5:在定理1的条件下,如果α(u0)是真参数,则,其中λ在式(12)中定义。
引理3、4、5的证明参考文献[2],这里不再详述。
定理1的证明:结合引理,对式(11)利用Taylor展开式得:

根据式(12)可以得到:

由上面三个式子定理1易证。
定理2的证明参考文献[6]。
4 结束语
本文介绍了协变量有误差的半参数变系数部分线性模型的似然推断,提出了经验似然在半参数误差模型中的应用。对于删失数据、缺失数据在广义线性模型、线型混合模型中的经验似然推断有所欠缺,还有待进一步的研究。

