筒仓静态储粮的边界压力及仓壁摩擦力试验研究

韩 阳，李东桥，陈家豪，静 行，段君峰



筒仓静态储粮的边界压力及仓壁摩擦力试验研究

韩 阳，李东桥，陈家豪，静 行，段君峰

（河南工业大学土木建筑学院，郑州 450001）

为了研究筒仓散装粮堆的边界压力和仓壁摩擦力的分布规律，研制了模型筒仓试验装置，基于仓体的微缝分离设计，实现各分离仓体受力的独立测量。以小麦为例，通过实测，发现不同装粮高度下，粮堆底部压力沿径向呈现不均匀分布特征，其不均匀分布程度随装粮高度逐渐增加；当装粮高度大于筒仓直径后，仓壁侧压力开始逐渐小于Janssen公式计算结果；而仓壁摩擦力在整个粮堆深度范围内均小于Janssen公式计算结果。试验表明，仓壁实测摩擦力与侧压力之比小于小麦与仓壁的摩擦系数，且随粮堆深度的增加不断变化，表明静态储粮下储料与仓壁边界之间尚未达到极限平衡状态；侧压力系数接近主动态，且小于主动土压力系数。研究结果可为散体物料压力理论提供参考。

筒仓；试验；压力；侧压力；竖向压力；摩擦力

0 引 言

粮食等散体物料具有复杂的力学特性。由于可以承受静态剪切力，导致其空间静应力σ不能简单地通过求解力平衡方程Ñ=ρg（假定密度恒定，g为重力加速度）得到，还需要确定物料自身的本构关系和问题的边界条件。目前，在筒仓粮食储料压力理论分析中，小麦等粮食物料还没有适宜的本构模型，而储料压力问题的边界条件也仅是简单定义仓壁边界和粮堆自由面两处，限制了储料压力问题的求解精度和适用范围。因此，仅以目前的条件难以推导普遍适用的粮食空间压力的计算方法。而试验研究又受到填料方式、仓体变形、填料时内置传感器偏移、粮堆内部应力及仓壁摩擦力难以观测等问题的困扰，有效且可重复的试验方案还很少见。

目前，许多研究都是在德国学者Janssen[1]提出的连续介质模型的基础上进行的，这个模型主要基于3个假设：1）储料的水平压力σ与竖向压力σ的比值（侧压力系数）保持不变，这个是对筒仓内散料应力状态的猜想；2）仓壁摩擦力τ与仓壁侧压力σ的比值恒等于储料与仓壁的摩擦系数0，即假定任意深度处储料与仓壁间均达到极限平衡状态，这个可以理解为对仓壁边界条件的猜想。这里，和0的取值受储料自身的物理参数、仓壁材质及储料充填过程等因素影响，而非由筒仓静态系统所确定的常数。如侧压力系数，Janssen公式中将其采用为朗肯[2]主动土压力系数，即与内摩擦角间存在=tan2(45°−/2)的关系。但目前的一些研究表明，在某些试验条件[3]下甚至会出现大于1这种偏离朗肯主动态的现象。而摩擦系数0则被定义为与储料和仓壁材质有关的常数，目前试验[4-7]测得的0都是散体物料与固体交界处的静摩擦系数（有些是滑动摩擦系数），即假定储料与仓壁间存在相对滑移的趋势。试验研究[8]发现，静态储粮下储料与仓壁间并未达到极限平衡状态，实测的仓壁摩擦力τ与侧压力σ之比在整个粮堆范围内均小于0，并且这个比值τ/σ沿粮堆深度不断变化。本研究将这种颗粒物质与其容器边界之间摩擦不充分的现象称为“仓壁的摩擦效应”，即仓壁摩擦力τ与侧压力σ的比值τ/σ是一个与粮堆深度有关的函数，而不是一个与无关的常数。

Janssen的第三点假设为粮堆任意水平面上竖向压力σ均匀分布，它的大小仅与有关。由于粮堆的内部应力难以观测，对于这个假设的合理性尚没有直接的试验验证。目前关于Janssen模型的研究[9-10]通常是间接测量粮堆底部边界处的储料压力，进而推测竖向压力σ与粮堆深度的关系。现阶段试验测量的多为堆底的平均应力，由于受难以固定传感器位置、填料时传感器受扰动等因素的影响，底部压力沿径向的分布情况尚缺乏行之有效的试验方法。

为更准确研究筒仓散装粮堆边界压力及仓壁摩擦力的分布规律，验证Janssen模型，本文设计了新型的筒仓模型试验仓，对不同装粮高度下粮堆底部的竖向压力沿径向分布情况、仓壁侧压力和摩擦力与粮堆深度的关系进行了试验研究，为散体物料压力理论和仓储结构研究提供有效的试验方法。

1 筒仓模型仓试验

1.1 模型仓

模型仓的设计思想主要基于仓体的微缝分离设计和各分离仓体受力的独立测量。仓体主要由3段相互分离的筒壁以及1个可自由升降的仓底板组成。仓底板与筒壁之间以及各部分筒壁之间都设有微缝，这样既能够使它们相互分离，又不会使粮食颗粒流出，如图1所示。

注：黑色圆形为力传感器安放位置。尺寸单位为mm。

模型仓装粮高径比可为2～4，直径约为一般粮食筒仓的1/20，可以对深仓和浅仓状态下储料压力开展试验研究。

筒壁用有机玻璃制成，总高度2 102 mm，内径480 mm，壁厚10 mm，标记有刻度，便于观察和测量装粮高度。上筒高1 000 mm，固定在钢架上，使上筒壁受到的摩擦力不向下传递；中筒高100 mm，由沿环向均布的3个力传感器支撑，测量中筒受到的摩擦力，并在内壁沿环向镶嵌3个土压力盒，测量中筒所受侧压力；下筒高1 000 mm，由沿环向均布的3个力传感器支撑，测量下筒壁受到的摩擦力。

仓底板用10 mm厚钢板制作，直径478 mm，分为4个同心圆盘（图1c），各圆盘间留有小于1 mm的缝隙，分别由力传感器支承（中心环1个，其他环各3个），可分别测量仓底不同部位承受的粮食压力，进而可分析仓底压力沿径向的分布规律；仓底板可升降，最大行程为1 000 mm。通过控制底板的升降，可使中筒位于粮堆的不同高度，从而可测量物料对仓壁任意高程的侧压力和摩擦力。

试验选用力传感器均为福建锐马电器制造有限公司生产的RM-S200型，准确度等级C3；土压力盒为溧阳超源仪器厂生产的BW型，准确度级别0.2%。编制了数据自动采集和分析系统，可采集仓底板各圆盘所受竖向压力、下筒所受摩擦力和中筒侧压力、摩擦力，系统界面如图1d所示。

1.2 试验方案

Janssen猜想给出的一个重要结论为：

式中为储料重力密度（N/m3），为筒仓半径（m）。根据Janssen的假设，粮堆深度（m）处储料竖向压力σ（kPa）均匀分布，且侧压力σ（kPa）与竖向压力σ（kPa）的比值恒定为侧压力系数，仓壁摩擦力（kPa）等于静摩擦系数0与侧压力σ（kPa）的乘积。

为验证上述Janssen猜想及假设，结合模型仓试验装置的特点及功能，制定了以下试验方案：

1）测试仓底板粮食竖向压力σ分布和仓壁摩擦力：仓底板置于模型仓底部固定不动，每次装粮约100 mm高，并对进粮质量精确称量，装粮至1 000 mm高。利用仓底板各自圆盘下设置的力传感器测试仓底板不同部位粮食压力，得到不同装粮高度下仓底压力σ的变化和沿径向的分布情况；利用支撑下筒壁的力传感器测量不同装粮高度下仓壁摩擦力的变化趋势。

2）测试粮食不同深度处对仓壁的侧压力σ和摩擦力：仓底板初始位置置于下筒顶部，一次性装粮1 000 mm高并称总量，仓底板每次下降50 mm，静置一段时间至各传感器数值稳定后，利用镶嵌在中筒内壁的土压力盒和支撑中筒的力传感器分别测量粮堆不同深度处储料对仓壁的侧压力σ和摩擦力。

1.3 小麦试样

储料选用河南荥阳小麦，根据《粮油检验容重测定》GB/T 5498-2013[11]、三轴压缩试验[12]和直剪试验[8]，测得小麦试样参数如表1所示。

表1 小麦试样参数Table 1 Wheat sample parameters

注：外摩擦角为小麦与模型仓仓壁材质（有机玻璃）间的外摩擦角。

Note: External friction angle is the external friction angle between the wheat and the material (PMMA) of the silo wall.

1.4 试验数据处理方法

根据方案1）进行重复试验4次，方案2）重复试验3次，数据均取各传感器均值，使用Excel2003进行数据处理及图形绘制；Minitab进行误差分析及数值拟合，其中误差棒为相同装粮高度（或粮堆深度）下，各次试验均值±标准差。

2 试验结果

2.1 粮堆底部竖向压力

仓内粮食总重力应等于模型仓底板各圆盘承受压力总值与筒壁所受总摩擦力值之和，可以此作为试验装置设计是否完善、传感器是否准确的依据。方案1）试验中装粮任意高程下粮食重力与力传感器总值间误差皆小于5%，为可接受范围内，一定程度上证明了数据的准确，表明试验有较好的可重复性。

取各次试验结果平均值，得到了不同装粮高度下仓底压力分布图，如图2所示。

图2 不同装粮高度下粮堆底部竖向压力

由图2可以看出，粮堆底部的储料竖向压力呈现出不均匀分布特征。随着装粮高度的增加，靠近仓壁处压力与仓中心处的压力差距逐渐明显。在小麦堆载高度小于0.4 m，即高径比小于1.0时，仓底各圆环压力值与小麦堆载高度近乎呈线性增加关系；当粮堆高度超过0.5 m后，随着小麦堆载高度的增加，各圆环压力值继续增大，但增加速度减慢。仓底压力曲线拐点（0.5 m）的出现，反映了浅仓与深仓仓底压力的区别。

2.2 仓壁侧压力

根据方案2）进行试验，记录了仓壁侧压力与粮堆深度之间的关系，并与一些经典公式[13]的结果进行对比，如图3所示。

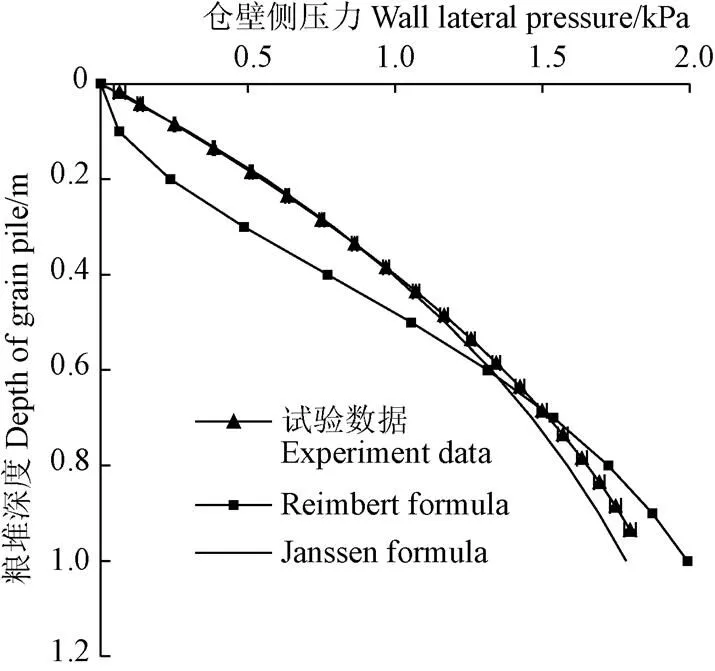
图3 仓壁侧压力与粮堆深度的关系

由于Reimbert公式是半经验公式，部分内容为试验曲线拟合得到，且其试验选取物料为砂，若不经任何修改，它的适用范围有限，故图3中，其结果与试验结果有较大偏差。Janssen公式结果在粮堆深度较小时与试验结果几乎一致；在粮堆深度大于筒仓直径（0.5 m）时则略小于试验结果。这个结果与一些文献[14-16]报道的相仿，即Janssen公式中得到的侧压力比实际值偏小，所以许多国家的规范[17-18]都在计算中乘以水平压力修正系数C以保证结构的安全。

2.3 仓壁摩擦力

仓壁摩擦力沿仓壁的分布可以直接由隔离的中筒测量得到，也可以由每次底板下降过程中由下筒壁测得的摩擦力的增量得到，如图4a所示。从图4a中可见二者基本一致，表明测试仪器工作正常。试验得到仓壁摩擦力与粮堆深度的关系如图4b所示。可以看到，试验结果与Janssen公式和Reimbert公式计算结果都有一定偏差。Janssen公式得到的摩擦力在整个粮堆深度范围内均大于试验结果。当粮堆深度小于0.6 m时，Reimbert公式计算得到的摩擦力小于试验结果；这之后，则大于试验结果。

图4 仓壁摩擦力与粮堆深度的关系

3 分析与讨论

3.1 堆底竖向压力分析

筒仓储料的静态压力有一种被称为“粮仓效应”[19-20]的奇异现象，即当粮堆达到某一高度后，堆底压力不再随装粮高度的增加而增加，而是趋于饱和。造成这种现象的原因为储料内部的剪切力、储料与仓壁间的摩擦力等在筒仓内形成拱效应，使储料的一部分重力转移到仓壁上。图5a和图5b分别绘制了仓底平均压力与装粮高度的关系及仓底不同区域竖向压力与装粮高度的关系。

图5 仓底压力与装粮高度的关系

从图5a中可以看到，在装粮高度较低时，粮堆底部的平均压力接近线性增长；当粮堆高度达到仓径(0.5 m)后，增加趋势逐渐变缓。图5b中，仓底不同区域处储料压力也呈现出不同程度的“粮仓效应”。当装粮高度小于0.2 m时，各圆环区域的压力曲线近乎重合；装粮高度大于0.3 m后，各环压力值开始出现区别，相同装粮高度下，越接近仓壁边界的圆环所承受的储料压力越小。三环压力（即仓壁边界处储料竖向压力）曲线与其余各环曲线区别较为明显，它很早地结束了线性变化阶段，进入趋于饱和的非线性变化阶段。而其余各环的变化趋势与它们距仓壁的距离有关：离仓壁越远，越晚结束线性变化。这点体现出仓壁摩擦的影响，即相同装粮高度下，仓壁摩擦对储料的影响是逐渐减弱的，距仓壁越远，储料间竖向切应力越小，这是造成粮堆底部竖向压力不均匀分布的主要原因。

3.2 仓壁摩擦效应

Janssen模型中假定仓壁摩擦力τ与侧压力σ的比值0恒定，其模型中隔离的储料薄片的竖向平衡方程中以0·σ表示摩擦力τ。本试验中测得的仓壁摩擦力τ明显小于Janssen公式中0·σ的结果，且τ/σ沿粮堆深度发生变化。本文以μ表示试验测得的摩擦力与侧压力的比值τ/σ，对图表进行无量纲处理，以粮堆深度与模型仓内径的比值/作为轴，μ与/的关系如图6所示。

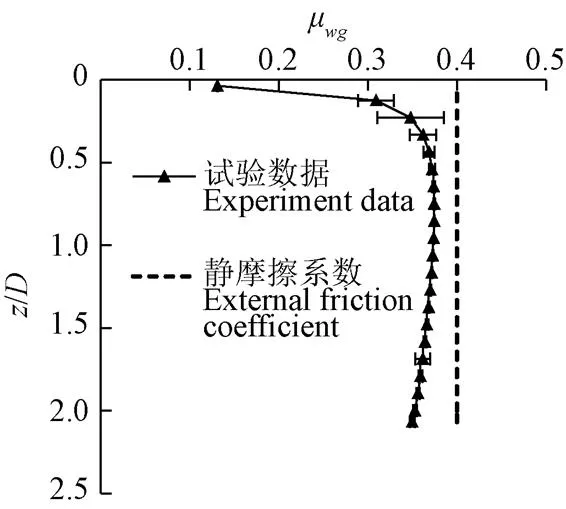
注：μwg表示试验测得的摩擦力与侧压力的比值τw/σr，z/D表示深度比，下同。

在图6中，当/小于0.3时，μ随着/的增加而线性增大；当/大于0.3而小于0.8时，μ非线性增大；其后到粮堆底面，μ又近似线性减小。μ在整个粮堆深度范围内均小于小麦与模型仓仓壁材料间的静摩擦系数0。这表明静态储粮下，储料与仓壁边界间并未达到极限平衡状态，即储料与仓壁间的摩擦并没有充分“动员起来”，所以Janssen模型中假定的仓壁边界条件（τ/σ恒定为静摩擦系数）与实际情况有一定偏离。本文将这种散体物料与其容器边界摩擦不充分的现象称为“仓壁的摩擦效应”。有些研究[21-22]通过“上拉仓壁”或“仓底板下沉”等方法来使试验仓的边界条件更接近Janssen模型，试验得到的结果也与Janssen吻合较好。但实际工程中，大多的粮仓几乎都是直接填料的，很难进行这样的后续处理。所以如果能确定静态储粮下τ/σ的值（或表达式），并以此改进Janssen的仓壁边界条件，会为仓储研究提供更准确的储料荷载。

3.3 侧压力系数

根据不同国家规范及学者们的研究[23-25]，侧压力系数有许多取值方法。如中国规范将其选取为主动土压力系数、美国规范采用静止土压力系数，而欧洲规范[26]则对静止土压力系数进行了修正。由于几种方法对值的计算结果偏差较大，学者们对其的选取问题仍有争议[27-30]。受测量方法的限制，目前的试验多以仓壁静摩擦系数0来估算值的下限，因为二者总是耦合在一起出现，以此验证Janssen猜想。但是如3.2节所述，颗粒材料与固体边界间摩擦力的分布规律本身就是一个十分复杂的问题，所以对侧压力系数的选取问题仍需多方面的验证。根据模型仓试验数据，本文略去边界效应影响，以装粮高度为的仓底压力近似表示粮堆深度处的竖向压力，以储料在仓壁处的侧压力与同一水平面的竖向压力之比作为仓壁处侧压力系数值，如图7所示。

图7 侧压力系数K与z/D的关系

在图7中，当/小于1.0时，随着/的增加而非线性增大；当/大于1.0后，值增速变缓，在粮堆底面，值又略有减小。在整个粮堆深度范围内，试验所得的侧压力系数接近主动态，但小于主动土压力系数tan2(45°-/2)，这点同样与Janssen猜想有所偏离。

3.4 对修正Janssen方程的建议

粮仓系统的仓壁摩擦及内部颗粒物质的应力状态是两个十分复杂的问题，因为试验偶然误差、储料密度随装粮高度变化等问题的存在，目前还很难解释它们的规律。就我们所做的有限元模拟[8]来说，两者的分布应与颗粒尺寸、筒仓直径、装粮高度及深度比等因素有关。

以试验测得的μ与侧压力系数相乘，得到μK与深度比/的关系，如图8a所示。图8a中，在粮堆深度比/小于1时，μK非线性增大，之后增加趋势趋于平缓；在/大于1.6后，又有所减小。虽然μK并非恒定，但可以看到在深度比大于1后，它开始围绕某一点波动，其上限为0.17，下限为0.15。取深度比1～2之间的试验结果进行数值拟合，发现本文模型仓试验的μK在0.159附近涨落。将μK拟合值代入Janssen模型，并将其结果与试验结果及Janssen公式计算结果对比，如图8b所示。可以看到，拟合结果与试验数据较为接近，Janssen公式计算结果结果则明显小于试验数据。结合3.2节及3.3节试验结果可知，Janssen对0和的选取有所偏大。

目前人们对Janssen模型的修正更多考虑的是如何选取适宜的压力修正系数或值的放大系数，通过增大计算值来保证结构的安全，而对μ和的分布规律的研究还比较少见。如果能进一步精确两者的分布函数或不同协议下的近似值，以此改进Janssen模型，也是一种较为可行的方法。

图8 试验数据与拟合结果的对比

4 结 论

通过自行研制的模型筒仓试验装置，以小麦为例，对Janssen猜想及Janssen模型的边界条件进行了验证，讨论了粮堆底部竖向压力、仓壁侧压力和摩擦力的分布规律，得出以下结论：

1）试验表明，仓底的竖向压力是不均匀分布的，并随着装粮高度的增加，不均匀分布的程度逐渐明显，靠近仓壁处压力与仓中心处的压力差距逐渐增大；仓底边界沿径向不同区域处的储料压力随粮堆高度的增加，均会出现一定程度的趋于饱和的现象，其变化趋势与观测点至仓壁距离有关。分析表明，仓壁摩擦力及储料间的切应力的共同作用是造成这些现象的主要因素。

2）试验表明，小麦深度小于筒仓直径时，仓壁侧压力与小麦堆深度呈线性增加关系，与Janssen公式计算值基本一致；当深度超过筒仓直径后，侧压力值与小麦堆深度呈非线性增大关系，增加速度减缓，表明粮堆深度与仓径比对仓壁侧压力的影响，试验数据略大于Janssen公式计算值。

3）试验所得的仓壁摩擦力小于Janssen猜想提出的的静摩擦系数与侧压力的乘积0·σ，并且仓壁摩擦力与仓壁侧压力的比值μ沿粮堆深度变化，在粮堆深度范围内均小于静摩擦系数0，说明静态储粮下储料与仓壁边界之间尚未达到极限平衡状态；试验所得的侧压力系数与μ的变化趋势相仿，同样在粮堆深度范围内不断变化，且小于主动土压力系数tan2(45°−/2)。本文试验中它们的乘积μK在深度比1～2之间围绕0.159波动，Janssen模型对二者的取值均有所高估，拟合结果表明进一步精确μ和的选取问题，是一种修正Janssen方程的可行方法。

试验结果表明，该模型试验仓运行方便，每次试验粮食质量与传感器测试误差皆在5%以内，试验可重复性较好。该模型仓和相关试验方案可为散体物料压力理论的试验研究提供简便可行的技术支持。

[1] Janssen HA. Experiments about pressures of grain in silos[J]. Z. des Vereines Deutscher Ingenieure, 1895, 39(35): 1045－1049.

[2] Rankine W J M. On the stability of loose earth[J]. Proceedings of the Royal Society, 1857, 147: 9－27.

[3] 李湘群，蒋亦民，彭政，等. Rankine被动应力状态粮仓的Janssen行为[J]. 山东大学学报：理学版，2010，45(9)：101－104.

Li Xiangqun, Jiang Yimin, Peng Zheng, et al. Janssen behavior of silos with Rankine passive stress[J]. Journal of Shandong University: Natural Science, 2010, 45(9): 101－104. (in Chinese with English abstract)

[4] 安蓉蓉. 粮食的内摩擦角、弹性模量及体变模量的试验研究[D]. 南京：南京财经大学，2010.

An Rongrong. Experiment Study on Angle of Internal Friction, Elastic Modulus and Bulk Strain Modulus of Grain[D]. Nanjing: Nanjing University of Finance and Economics, 2010. (in Chinese with English abstract)

[5] 彭政，王璐珠，蒋亦民. 颗粒物质与固体交界面静摩擦系数的测量与分析[J]. 山东大学学报：理学版，2011，46(1)：42－45.

Peng Zheng, Wang Luzhu, Jiang Yimin. Measurement and analysis of static friction coefficient on a granular-solid interface[J]. Journal of Shandong University: Natural Science, 2011, 46(1): 42－45. (in Chinese with English abstract)

[6] 许启铿，金立兵，王录民，等. 粮食力学参数的试验研究[J]. 河南工业大学学报：自然科学版，2010，31(1)：18－21.

Xu Qikeng, Jin Libing, Wang Lumin, et al. Research on the determination of mechanical parameter of grains[J]. Journal of Henan University of Technology: Natural Science Edition, 2010, 31(1): 18－21. (in Chinese with English abstract)

[7] 程绪铎，陆琳琳，石翠霞. 小麦摩擦特性的试验研究[J]. 中国粮油学报，2012，27(4)：15－19.

Cheng Xuduo, Lu Linlin, Shi Cuixia. The experimental research on friction properties of wheat[J]. Journal of the Chinese Cereals and Oils Association, 2012, 27(4): 15－19. (in Chinese with English abstract)

[8] 陈家豪. 散装粮堆空间压力场理论与试验研究[D]. 河南：河南工业大学，2017.

Chen Jiahao. The Theoretical and Experimental Study on the Spatial Pressure Field of Granular Grain pile[D]. Henan: Henan University of Technology, 2017. (in Chinese with English abstract)

[9] 蒋亦民，郑鹤鹏. 一种颗粒底部压力不趋向饱和的粮仓系统[J]. 物理学报，2008, 57(11)：7360－7366.

Jiang Yimin, Zheng Hepeng. A silo of which the pressure on the bottom of granular matter does not go to saturation[J]. Acta Physica Sinica, 2008, 57(11): 7360－7366. (in Chinese with English abstract)

[10] 李智峰，彭政，蒋亦民. 粮仓内颗粒压力的测量: Janssen行为及其偏差[J]. 物理学报，2014，63(10)：296－303.

Li Zhifeng, Peng Zheng, Jiang Yimin. Measurements of granular pressure in silo: Janssenbehaviour and deviation[J]. Acta Physica Sinica, 2014, 63(10): 296－303. (in Chinese with English abstract)

[11] GB/T 5498-2013. 粮油检验容重测定[S].

[12] 许启铿，陈家豪，王录民. 小麦力学参数的三轴压缩试验研究[J]. 河南工业大学学报：自然科学版，2015，36(5)：101－105.

Xu Qikeng, Chen Jiahao, Wang Lumin. Mechanical parameters of wheat in triaxial compression tests[J]. Journal of Henan University of Technology: Natural Science Edition, 2015, 36(5): 101－105. (in Chinese with English abstract)

[13] Reimbert M L, Reimbert A M. Silos: Theory and Practice[M]. Clausthal: Trans Tech Publictions, 1976.

[14] 陈长冰. 筒仓内散体侧压力沿仓壁分布研究[D]. 合肥：合肥工业大学，2006.

Chen Changbing. Research on Distribution of Lateral Bulk-Solid Pressures on Silos’ walls[D]. Hefei: Hefei University of Technology, 2006. (in Chinese with English abstract)

[15] 刘定华，王建华，杨建斌. 钢筋混凝土筒仓侧压力的试验研究[J]. 西安建筑科技大学学报，1995(1)：8－12.

Liu Dinghua, Wang Jianhua, Yang Jianbin. An experimental study of the lateral pressure on the wall of reinforced concrete silo[J]. Journal of Xian University of Architecture and Technology, 1995(1): 8－12. (in Chinese with English abstract)

[16] 刘定华，郝际平. 钢筋混凝土筒仓仓壁侧压力的研究[J]. 建筑结构学报，1995(5)：57－63.

Liu Dinghua, Hao Jiping. Research on lateral pressure upon wall of reinforced concrete silo[J]. Journal of Building Structures, 1995(5): 57－63. (in Chinese with English abstract)

[17] GB50077-2003. 钢筋混凝土筒仓设计规范[S].

[18] ACI Committee 313-97. Standard practice for design and construction of concrete silos and stacking tubes for storing granular materials[S].

[19] 陆坤权，刘寄星. 颗粒物质(上)[J]. 物理，2004，33(9)：629－635. Lu Kunquan, Liu Jixing. Static and dynamic properties of granular matter(I)[J]. Physics, 2004, 33(9): 629－635. (in Chinese with English abstract)

[20] 王晶. 不同维度下颗粒链的粮仓效应[D]. 北京：北京理工大学，2016.

Wang Jing. Bottom Stress of Static Packing of Granular Chains in 2D and 3D Silos[D]. Beijing: Beijing Institute of Technology, 2016. (in Chinese with English abstract)

[21] Vanel L, Clément E. Pressure screening and fluctuations at the bottom of a granular column[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 1999, 11(3): 525－533.

[22] Vanel L, Claudin P, Bouchaud J P, et al. Stresses in silos: Comparison between theoretical models and new experiments[J]. Physical Review Letters, 1999, 84(7): 1439－1442.

[23] Jaky J. The coefficient of earth pressure at rest[J]. Journal for Society of Hungarian Architects and Engineers, 1944(5): 355－358.

[24] 张家康，黄文萃，姜涛，等. 筒仓贮料侧压力系数研究[J]. 建筑结构学报，1999，20(1)：71－74.

Zhang Jiakang, Huang Wencui, Jiang Tao, et al. Study on lateral pressure ratio of stored material in silo[J]. Journal of Building Structures, 1999, 20(1): 71－74. (in Chinese with English abstract)

[25] 曾丁，黄文彬. 筒仓壁压的有限元分析[J]. 农业工程学报，1998，14(2)：44－48.

Zeng Ding. Huang Wenbin. Finite element analysis of silo wall pressure[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 1998, 14(2): 44－48. (in Chinese with English abstract)

[26] BS EN1991-4:2006. Eurocode 1-Actions on structures-Part 4: Silos and tanks[S].

[27] 冯云田，华云龙. 适用于柔性圆筒仓的修正的Janssen公式[J]. 中国农业大学学报，1996(4)：107－111.

Feng Yuntian, Hua Yunlong. Modified Janssen formula for flexible circular bins[J]. Journal of China Agricultural University, 1996(4): 107－111. (in Chinese with English abstract)

[28] 曾丁，郝保红，黄文彬. 筒仓静态壁压的有限元分析[J]. 中国粉体技术，2000(5)：6－10.

Zeng Ding, Hao Baohong, Huang Wenbin. Finite element analysis of static wall pressure of silo[J]. China Powder Science and Technology, 2000(5): 6－10. (in Chinese with English abstract)

[29] 陈长冰. 考虑仓壁弹性的粮食钢筒仓侧压力系数修正[J]. 中国农机化学报，2006(3)：82－83.

Chen Changbing. Lateral pressure ratio of food steel silos based on considering the wall elasticity[J]. Journal of Chinese Agricultural Mechanization, 2006(3): 82－83. (in Chinese with English abstract)

[30] 孙珊珊，赵均海，张常光，等. 深仓和浅仓储料侧压力新解[J]. 广西大学学报：自然科学版，2018，43(1)：168－177.

Sun Shanshan, Zhao Junhai, Zhang Changguang, et al. New solution for lateral pressure of silos and bunkers[J]. Journal of Guangxi University: Natural Science Edition, 2018, 43(1): 168－177. (in Chinese with English abstract)

Experimental study on boundary pressure and wall friction under static grain storage in silo

Han Yang, Li Dongqiao, Chen Jiahao, Jing Hang, Duan Junfeng

(,450001,)

The authors participated in the design of the silo model test facility, which can be used to measure the storage force of the grain heap, such as the bottom pressure, the side wall pressure and the friction force of the bulk grain heap. The self-designed silo model was 480 mm in diameter and 2 102 mm high. The silo wall, constructed of organic glass, was composed of 3 separate parts. There is a 1-mm thick gap between each part of the walls to prevent the outflow of grain. The 3 parts of the wall were named Top Wall (l 000 mm high, fixed on the steel frame), Middle Wall (100 mm high) and Upper Wall (1 000 mm high). The silo bottom, which can be raised and lowered, was divided into 4 parts (1 concentric circle and 3 concentric rings). The Top Wall, the Middle Wall and each parts of silo bottom were supported on three force sensors to measure the wall friction as well as the vertical pressure on the floor. Three earth pressure cells were embedded in the middle line of the Middle Wall to measure the wall lateral pressure. Two experimental schemes were carried out. No.1 scheme is that: Fill the silo model with wheat to a height of 100 mm at each time until the height of the wheat reached 1 000 mm. Record the data obtained from each of the force sensors supported under each part of the silo bottom as well as the force sensors supported under the Upper Wall of each grain height. This scheme is designed to measure the radial distribution of bottom pressure under different grain heights. The No.2 scheme is that: Fill the silo model with wheat to a height of 1 000 mm and then raise the flat bottom to the lower edge of the Middle Wall. Drop the bottom by 50 mm at each time. Meanwhile, record the data obtained from the earth pressure cells embedded in the Middle Wall and the data obtained from the force sensors supported under the Middle Wall at difficult depths of wheat. The distribution of the storage force at the boundary was measured in the experiment. The rationality of the model test data is verified by compared with the classic theory. Combined with the experimental data, it is found that the bottom pressure of silo grain heap presents the uneven distribution characteristics of “large in middle and small on sides”, and the uneven distribution degree is gradually obvious with the increase of grain loading height. The lateral pressure of silo wall is slightly larger than that of Janssen formula when the depth is more than 0.5 m. The friction of the side wall is larger than that of Janssen formula along the whole depth of wheat.Andthe value of the friction coefficient between the grain and the silo wall is smaller than external friction coefficient measured by directly sheared tests along the whole depth of wheat. It proved that the value of wall friction calculated by Janssen formula is larger than what it really is and the state between the wheat and silo wall haven’t reach the limit equilibrium. The lateral pressure coefficient measured by experiment is closed to Rankine's main dynamic and is less than active earth pressure coefficient. The experiment results show that the model silo test device has good repeatability, and it can provide a simple and feasible technical support for the theory of storage pressure.

silo; experiment; pressure; lateral pressure; vertical pressure; friction

韩 阳，李东桥，陈家豪，静 行，段君峰. 筒仓静态储粮的边界压力及仓壁摩擦力试验研究[J]. 农业工程学报，2018，34(13)：296－302. doi：10.11975/j.issn.1002-6819.2018.13.036 http://www.tcsae.org

Han Yang, Li Dongqiao, Chen Jiahao, Jing Hang, Duan Junfeng. Experimental study on boundary pressure and wall friction under static grain storage in silo[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(13): 296－302. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.13.036 http://www.tcsae.org

2018-04-04

2018-05-10

国家自然科学基金（51608176）

韩 阳，教授，博士生导师。研究方向为仓储结构及防灾减灾工程。Email：hanyangh@126.com

10.11975/j.issn.1002-6819.2018.13.036

TS210

A

1002-6819(2018)-13-0296-07