无刷直流电动机无传感器换相误差自校正方法
金 浩,殷 英,苗 欣,李言民,梁建英
(中车青岛四方机车车辆股份有限公司,青岛 266111)
0 引 言
无刷直流电动机(以下简称BLDCM)具有速度控制精度高、安全、高效等特点,是驱动磁悬浮控制力矩陀螺高速转子的理想选择[1]。
无刷直流电动机通过位置传感器检测转子位置进行换相,然而位置传感器的安装精度对电动机的运行性能有较大的影响,增加了系统复杂程度[2,3]。
无刷直流电动机无位置传感器技术可以避免上述缺点,无刷直流电动机无位置传感器换相方法分为位置检测法、位置估算法。其中位置检测法包含反电动势过零点法[4]、反电动势三次谐波检测法[5]等。反电动势过零点方法简单,易于实现,目前应用广泛,但过零点信息受到诸多因素影响(硬件延时、软件延时),容易引起换相失准[6]。文献[7]采用反电动势积分法,换相精度得到提高,但是这种方法受制于系统采样频率,容易受到PWM信号和二极管反向续流等因素干扰,造成换相误差累积。文献[8]中,杨影对假中性点采样积分在中低速下取得了良好的控制效果,同样信号积分精度受到的影响较多。电感检测法[9]利用有效电感与转子位置的关系来确定换相时间,对于小电感电机而言,检测信号微弱,可行性较低。转子位置估计法又分为滑模观测器法[10]、神经网络法[11]、扩展卡尔曼滤波法[12]等。对于滑模观测器法,在控制到达稳态时会存在固有的抖振现象[13]。文献[14]利用饱和函数代替开关函数,较好地减弱了滑模控制存在的抖振问题。人工神经网络[15]的方法具有自适应、自学习的特点,但是需要采用较长时间的训练过程,计算过程较复杂。
本文采用反电动势过零点法实现无位置传感器换相,分析了端电压与中性点之间电压差信号对称性的特点,并提出了一种电路来获得该电压差信号,以该电压差为反馈信号在特定时刻采样,以采样电压相等为目标建立换相误差校正回路,实现换相误差的校正。
1 无位置传感器无刷直流电动机原理
1.1 无刷直流电动机数学模型
如果电机电感较小,采用传统的三相桥驱动电路进行PWM调制会引起严重的调制脉动,影响控制精度,增加系统功耗。因此,对于小电感的磁悬浮控制力矩陀螺,在高速电机前端添加降压斩波电路(Buck)环节,电机的拓扑结构如图1所示。

图1 无刷直流电动机拓扑结构
建立电机三相端电压平衡方程:
式中:ea,eb,ec为每一相的反电动势;ua,ub,uc为电机等效端电压;uN为中性点电压;ia,ib,ic为电机相电流;L为电机的相电感,R为等效相电阻,M为等效互感。
为分析方便,利用反电动势同频基波来近似表示无刷直流电动机反电动势,可以近似表述如下:
式中:e为基波峰值;ω为电角速度。
以A相为例分析,由于电机采用的是两两导通方式,由式(1),当A相为导通相时:
当A相为非导通相时,ia为零,则:
ua-uN=esin(ωt)(4)

1.2 输出反馈信号的电路结构
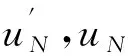
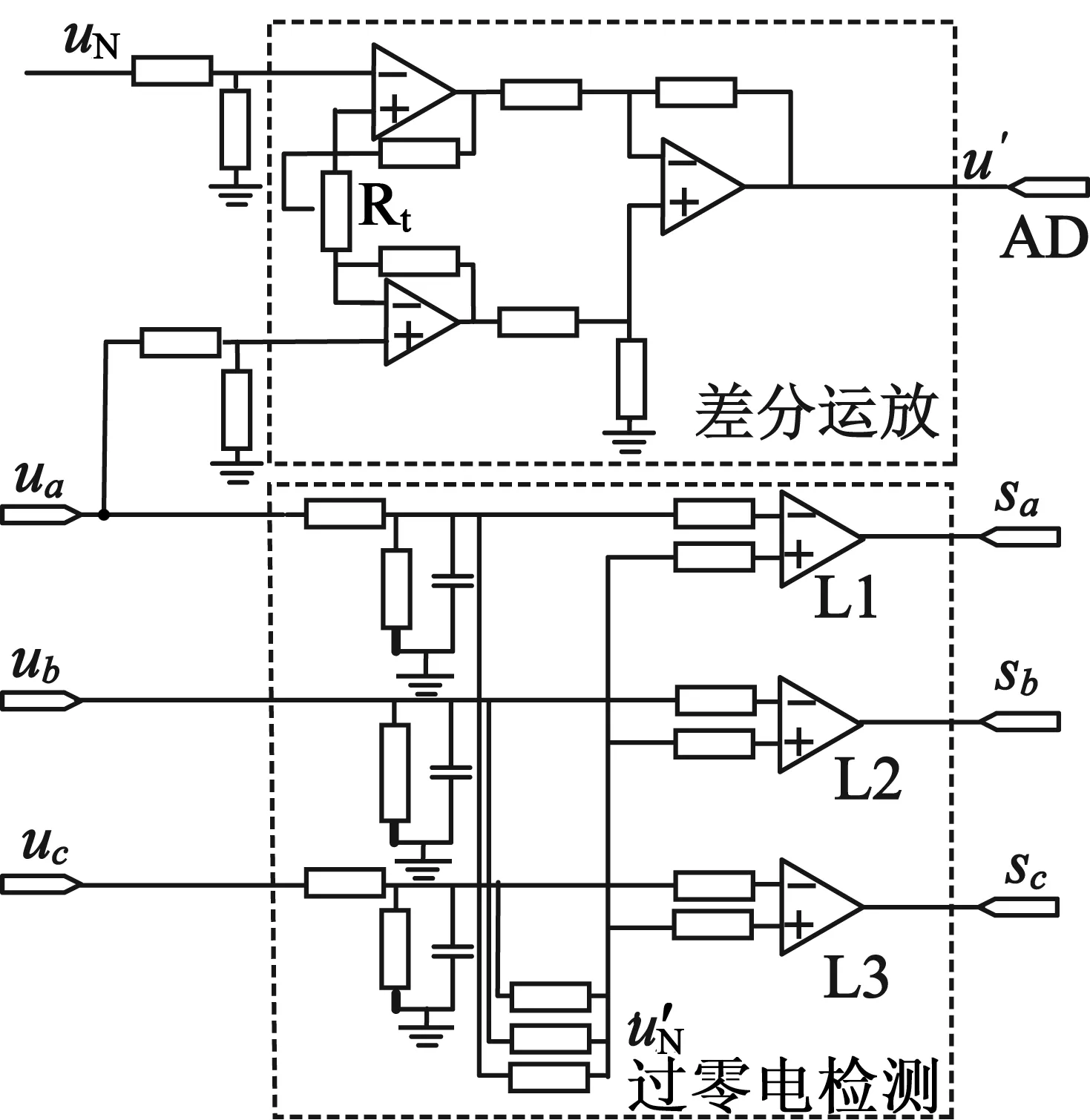
图2 换相误差自补偿方法的硬件电路

在图2上部虚线框的差分运放电路内,将ua和中性点uN引出,分压后送入仪表放大器中作差,可以获得校正所需的反馈信号u′,在A相导通和关断时刻采样u′,以2次采样电压相等为控制目标输入至控制回路,即可实现校正换相误差,补偿滞后角。
2 电机换相误差自校正控制方法
2.1 换相误差与反馈量分析
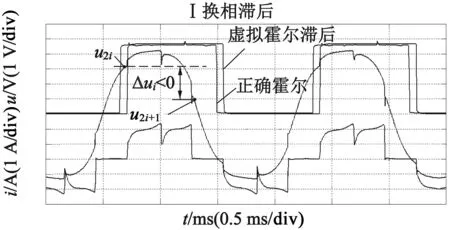
假设换相滞后角为α,考虑到电机绕组导通瞬间会产生续流,这种续流会引起换相点处u′的波动,若直接采样换相点处u′,不能真实反映换相误差大小。假设tc为额定转速下续流时间,为避开续流,可将A相模拟霍尔信号Sha超前τ=2max(tc),将B相模拟霍尔信号Shb滞后τ,分别产生新的方波信号(如图3~图5中虚线方波)并将这2个方波信号的上升沿作为采样中断信号,在中断产生时采样u′,避开了续流影响,同时保证了采样点依然分布在A相导通区间前后对称位置。
续流时间tc可以由如下公式得到[17]:
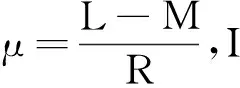
由于2π/3导通区间的中心位置偏离反电动势波峰α角度,A相两侧采样的u′分别为u2i,u2i+1,此时u2i,u2i+1会有一定的差值,该电压差值反映了换相误差α的信息。
综上,如图3~图5,设T为电周期,相邻采样间隔时间Δt=T/3+2τ,采样点即为Δt区间两端,由式(6)可得到第i次补偿控制的反馈量电压差Δui:
式中:ωt=2kπ,k=0,1,2,3,…;i=0,1,2,3,…。
由图可见u2i,u2i+1采样点恰好分布在第三路模拟霍尔信号Shc=1,Shc=0区间内,因此在采样时可以将Shc引入处理器,利用式(7)就可以得到控制的反馈量Δui:
将式(6)整理得:
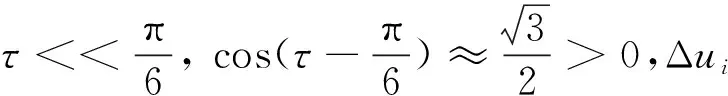
1) 换相准确,由图3可见,第i次采样时αi=0,

图3 换相准确时u′与模拟霍尔信号、采样中断信号关系
A相Δt区间两端波形对称,得到第i次控制反馈量:
采样点处反电动势电压相等,即在A相Δt两侧采样u′电压差为零,此时需要补偿的误差角度为零。
2) 换相滞后,由图4可见,第i次采样时αi<0,

图4 换相滞后时u′与模拟霍尔信号、采样中断信号关系
A相Δt范围整体向右偏离|αi|角度,u′两侧波形不再对称,得到第i次控制反馈量:
此时相位滞后造成2次采样点u′大小不相等,补偿的角度为负值,且|Δui|随着|αi|的减小而减小,并趋近于零。
3) 换相超前,由图5可见第i次采样时αi<0,A

图5 换相超前时u′与模拟霍尔信号、采样中断信号关系
相Δt范围整体向左偏离|αi|角度, 两侧波形不再对称,得到第i次控制反馈量:
相位超前造成2次采样点u′大小不一致,此时补偿角度为正值,且|Δui|随着|αi|的减小而减小,并趋近于零。
综上,当换相点偏离准确位置αi角度,A相导通区间两侧的采样中断信号以同样方向偏离αi角度,在导通前后对称位置获取u′作差得到Δui,其中,|Δui|∝|αi|,|Δui|的大小反映换相误差的大小,并且Δui的符号反映换相超前或者滞后。
2.2换相偏差实时补偿
将产生的补偿量与过零点延时30°时相叠加,得到过零点延时时间ρi=30°+ψi,建立增量式离散PI控制函数如下:
ψi=kp(Δui-Δui-1)+kiTΔui+ψi-1(12)
式中:kp为比例环节系数;ki为积分环节系数;T为控制周期;Δui,Δui-1分别为第i,i-1次控制的反馈值;ψi-1为i-1次输出换相误差补偿量。
如果计算得到的反馈信号Δui=0,经过控制器PI控制算法后,输出的补偿角度为ψi=0,表明换相角度不需要校正。
如果在第i次计算得到的反馈信号Δui<0,此时滞后的换相角度αi>0,经过控制器的PI控制环节输出的ψi<0,叠加到换相时间中,|Δui|将逐渐减小并且趋近于零,与此同时,换相误差αi收敛并趋近于零。
与上文分析一致,当第i次采集反馈控制量Δui>0,表明电机使用超前角换相,对应的αi<0,经过控制器控制输出的补偿角ψi>0,补偿过程中Δui变小,并向0趋近,超前角αi从负的角度向零收敛,换相误差角相应减小,电机相电流更加平整,换相转矩脉动削弱。
3 实验验证
为了验证本文无位置传感器无刷直流电动机换相误差自校正方法的有效性,采用本课题组研制的双框架磁悬浮控制力矩陀螺高速电机进行实验验证,实验分别在3 000r/min,6 000r/min转速下人为给定换超前角α=-15°,相滞后角α=+15°进行,下文给出了相关信号波形、控制收敛至稳态的过程曲线等。
系统的相关参数如表1所示,实验装置如图6所示。

表1 系统参数

图6 双框架磁悬浮控制力矩陀螺
如图7(c)所示,在换相误差控制进入稳态时,某一时刻人为给定给电机换相α=15°滞后角,由于换相滞后角α的引入,对u′的采样点随滞后角瞬间向时间轴正方向移动15°(图7(a)),分别在u2i,u2i+1位置分别取样,参照上文分析计算Δui=u2i+1-u2i<0,此时对应图7(b)偏差电压约为-1.2V。采用本文的方法,对误差进行闭环校正,将Δui反馈至控制环节输入端,随着控制的进行,Δui逐渐减小并向零收敛;与此同时,过零点延时角度向30°附近收敛。从过程来看,换相点收敛至准确位置仅需要50步左右,收敛过程平稳快速。从控制目标来看,换相时间最终在30°位置,达到了换相自校正的控制目标。同样对于换相超前过程,人为给定α=-15°,经过控制环节后,收敛过程约为35步左右,Δui(图7(e))、过零点延时时间(图7(f))与滞后换相时的收敛过程基本一致,换相误差控制效果明显。
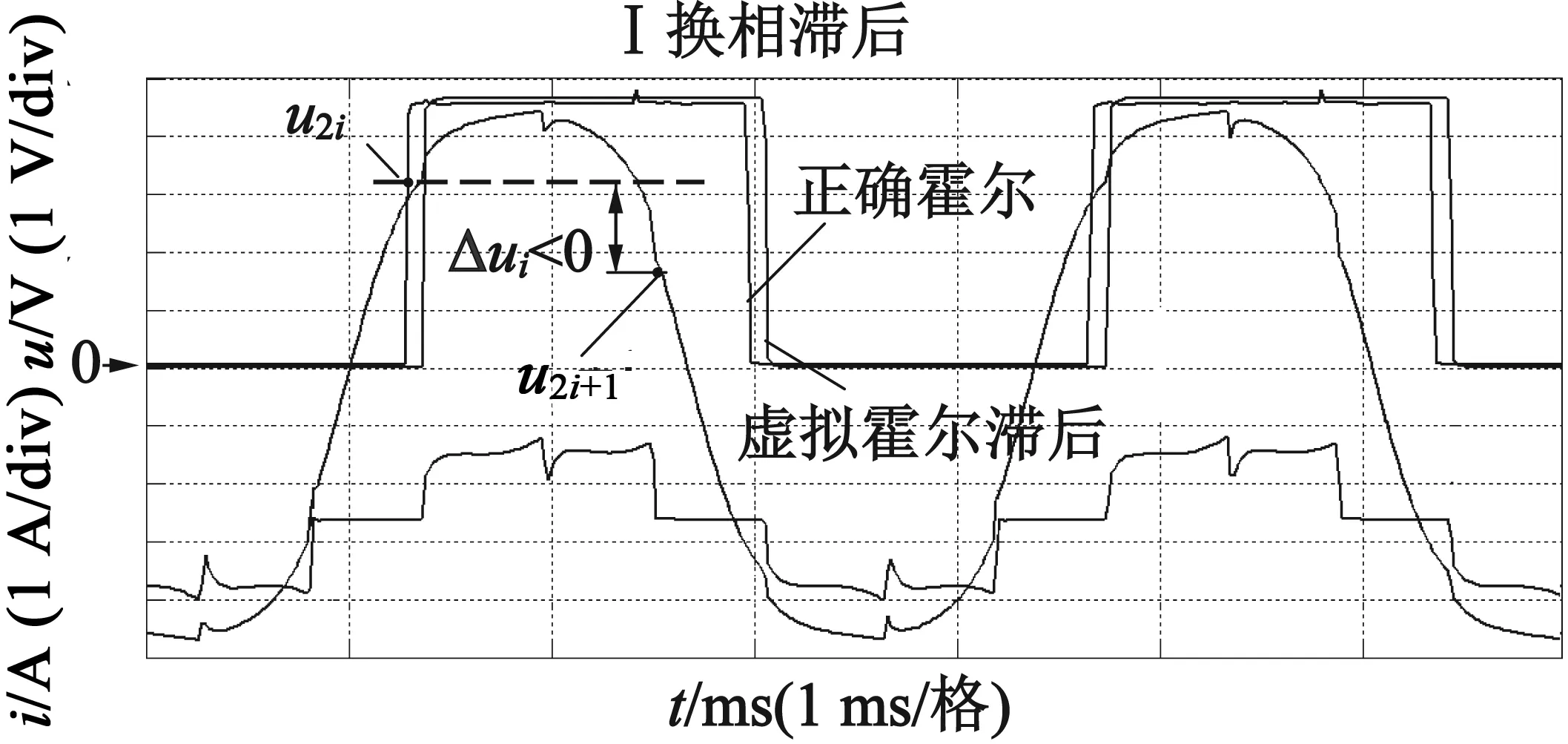
(a) 换相滞后采样原理
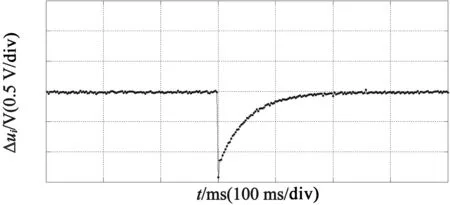
(b) 换相滞后Δui 收敛过程
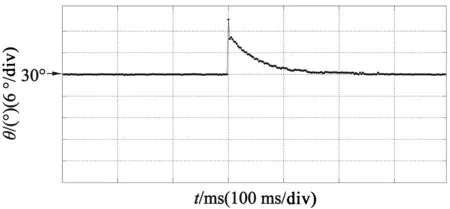
(c) 换相滞后过零点延时时间

(d) 换相超前采样原理

(e) 换相超前Δui 收敛过程

(f) 换相超前过零点延时时间图7 3 000 r/min转速下的换相滞后Ⅰ、超前Ⅱ的采样原理、收敛过程、过零点延时时间收敛过程
由图8可见,6 000r/min转速下,同样人为给定15°的换相偏移量,在换相滞后时,收敛过程与3000r/min转速的收敛过程基本一致,收敛过程约为40步左右;在超前换相时,校正至稳态会存在一部分噪声,通过优化控制系数、增加数字滤波等方式即可以减少这种抖动。
(a) 换相滞后采样原理
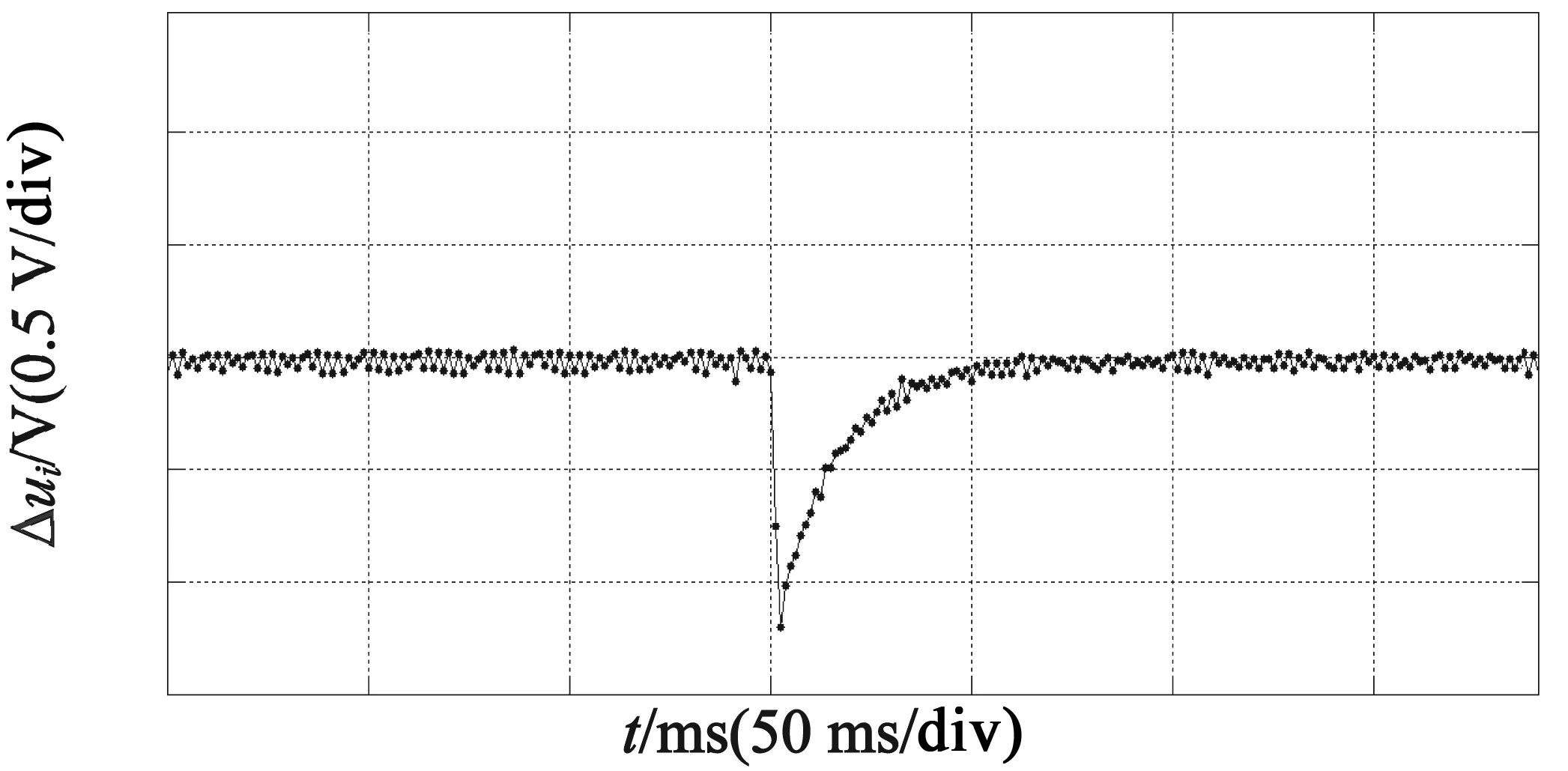
(b) 换相滞后Δui 收敛过程

(c) 换相滞后过零点延时时间

(d) 换相超前采样原理
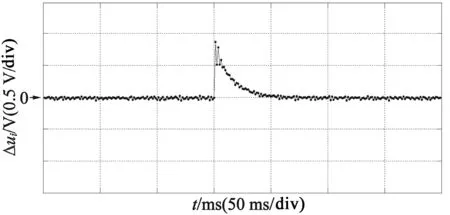
(e) 换相超前Δui 收敛过程

(f) 换相超前过零点延时时间图8 6 000 r/min下的换相失准的采样原理、Δui收敛过程、过零点延时时间收敛过程
从图9可以看出,控制进入稳态时,u2i,u2i+1取样位置位于A相开通和关断前后对称位置,电压差Δui为零,控制效果与3 000r/min转速基本一致。

(a) 3 000 r/min转速下

(b) 6 000 r/min转速下图9 3 000 r/min,6 000 r/min转速下换相误差校正后采样原理
4 结 语
本文采用简单实用的反电动势过零点延时30°换相方法,同时利用无刷直流电动机换相误差αi与u′的关系,建立误差校正回路,以Δui=0为控制目标,实现了换相误差的自校正,方法效果理想,降低了换相失准引起的续流作用,提高了电机性能。
对于误差控制稳态时存在抖动等问题,可以通过模型调节合适的PI参数解决。此外,在转速变化明显的场合,对换相误差的控制快速性、稳定性要求较高,利用先进的控制方法替换PI控制也是尚待改进的方向。

