基于VMD的超声波电动机退化特征提取研究

陈柏言，李洪儒，安国庆,3，许葆华

(1.陆军工程大学，石家庄 050003;2.中国人民解放军638501部队，白城 137001；3.河北科技大学，石家庄 050018)

0 引 言

随着维修理论和相关技术的发展，以故障预测技术为核心的基于状态的维修，引起许多专家学者的重视[1]，准确地提取出设备的退化特征是故障预测的基础。超声波电动机(以下简称USM)是现代航空航天和新型军事装备领域具有广阔应用前景的新型微特电机[2]，其作为系统的动力输出来源，能否正常工作直接关系到整个系统的工作状态。因此，提取其退化特征对超声波电动机故障预测具有重要意义，从而保障整个系统的安全有效运转。

超声波电动机在运转过程中，其定子结构中的压电陶瓷受到相位相差90°两相高频电压的激励作用，转化为定子的高频振动并产生行波，电机转动主要依靠定子与转子之间通过摩擦材料所产生的摩擦力驱动[3]。由于压电陶瓷材料本身硬而脆的特性加之长时间受到高频电的激励作用，在电机运转时极易开裂，是导致电机故障的主要原因之一[4]。定子的振动出现异常是电机性能退化的直接表现，压电陶瓷上的孤极反馈电压信号能够反映定子的振动状态[5]，因此孤极信号中隐含着丰富的状态信息。

退化特征提取是实现超声波电动机故障预测的关键环节，所提取的退化特征性能直接影响故障预测的结果，信号处理的目的就是为了更好地揭示蕴含在原始信号中的潜在信息。小波变换和自适应时频分析的方法常用于故障诊断和故障预测领域，小波变换由于小波基与分解尺度需依靠人为经验来确定，至今仍未有明确的选择标准，造成其自适应性较差；经验模态分解(EMD)方法作为一种最为经典的时频分析方法，其容易造成模态混叠和端点效应的问题，并且难以分解窄带内的多成分信号[6]。变分模态分解(以下简称VMD)方法[7]具有较好的数学理论基础并已在相关领域开始应用，该方法能够依据滤波原理将频带进行自适应划分并按照此划分结果进行分解，Liu[8]将VMD和去趋势波动分析相结合用于信号去噪，去噪效果均优于EMD去噪和小波去噪；Mert[9]在医学领域利用VMD对心电图(ECG)信号进行特征提取并利用多种分类器验证所提特征的有效性能；Wang[10]在转子系统中利用VMD成功地检测出由于摩擦引起的冲击。

针对超声波电动机退化特征提取问题，本文采用超声波电动机的孤极信号作为状态监测信号，并通过VMD信号处理方法，提取能够反映超声波电动机故障程度不断加剧的退化特征，通过支持向量机(以下简称SVM)模型验证退化特征反映退化状态的识别能力。最后，利用超声波电动机的孤极信号测试数据对本文所提出的方法进行验证。

1 超声波电动机

1.1 结构组成和工作原理

超声波电动机是20世纪80年代迅速发展和应用的一种新型微特电机，其组成结构如图1所示。整个电机由外壳、底座、轴、转子结构(由转子和依附在转子上的摩擦材料组成)和定子结构(由定子弹性体和压电陶瓷组成)5部分组成，能够满足微特电机中诸多新要求。

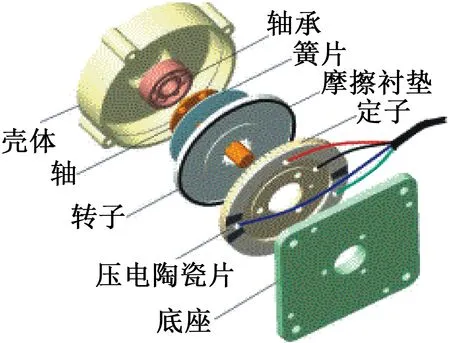
图1 超声波电动机组成结构图

超声波电动机的运转机理是定子上的压电陶瓷片通电后产生的振动，将电能转化为振动的机械能，定子结构中的压电陶瓷受到相位相差90°两相高频电压的激励作用，转化为定子的高频振动进而形成行波，通过定子和转子间的摩擦作用，推动转子朝着与行波传播方向相反的方向转动，如图2所示，定子与转子之间通过摩擦材料所产生的摩擦力使电机转动并驱动负载。

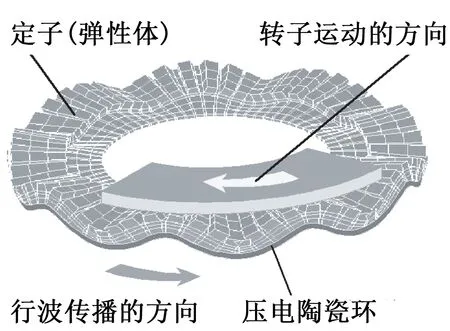
图2 行波和转子的运动方向图

1.2 故障分析

超声波电动机定子压电陶瓷片属脆性材料，断裂韧性低[11]，其厚度一般在0.5～1 mm之间[12]。电机在工作过程中，工作频率在机械共振频率附近的频段，定子的振幅比较大，有可能降低压电陶瓷片的抗拉强度，导致轻微开裂，进一步扩展裂纹[13]。另外，定子金属弹性体同压电陶瓷粘结时，表面处理不当、涂胶不均匀、加压不正确等都常导致粘结层出现缺胶或者气泡现象，并在放电火花的作用下演变为压电陶瓷断裂失效[14]，直接造成电机无法继续正常运转。电机一旦出现了故障，不仅会损坏电机本身，更重要的是会导致整个系统无法继续正常工作。超声波电动机动力来源为定子的高频振动，分析压电陶瓷片的振动状态，就能够准确快速地判断超声波电动机的退化状态，本文将孤极信号作为监测信号，进而从中提取有效的退化特征。

2 变分模态分解

VMD信号处理方法的目的是将信号分解为多个变分模态分量，通过多个维纳滤波器将信号实现频带上的自适应划分，并根据划分结果将复杂信号分解为多个IMF分量信号，并且每个固有模态分量(以下简称IMF)分量为调幅调频(AM-FM)信号[15]。VMD的具体方法如下[7]：

VMD将每个模态重新定义为AM-FM信号，表达式：

uk(t)=Ak(t)cos[Φk(t)](1)

式中：Ak(t)为uk(t)的瞬时幅值；ωk(t)为uk(t)的瞬时频率。VMD能够将输入信号f分解为各个模态分量，分解过程中通过各个模态的中心频率和带宽的反馈调整变化，最终将各个模态的分量的频域特性转化为某一中心频率处附近的有限带宽，其变分模型：

式中：uk代表分解得到的k个有限带宽IMF分量；ωk为各IMF分量的频率中心；δ(t)为脉冲函数。

引入二次惩罚因子α和Lagrange乘法算子λ(t)求上述问题，扩展的Lagrange表达式：

L({uk},{ωk},λ)=

更新λn+1的表达式：

综上所述，VMD算法[7]步骤如下：

(2) 根据式(5)～式(7)分别更新uk，ωk和λ；

(3) 对于给定判别精度ε>0，若满足迭代停止条件：

即可得到k个IMF分量，完成信号频带的自适应分割；否则，循环步骤(2)，直至满足迭代停止条件。

3 基于VMD的超声波电动机退化特征提取

3.1 超声波电动机退化特征提取方法的步骤

通常提供电机工作的电源电压为50Hz的交流电，而超声波电动机工作频带处于高频段，电机的转频通常较低，多种低频信号和高频信号会不可避免地会出现多种信号调制现象，电机的动力来源为定子的高频振动，因此必须使用信号处理的方法将高频成分从复杂的孤极信号中分离出，通过对高频信号的分析实现退化特征提取，进一步通过SVM验证退化特征的有效性。

本文研究的超声波电动机退化特征提取方法如图3所示。首先对超声波电动机孤极信号进行采集，通过VMD信号处理方法将反映定子振动状态的高频信号提取出来，以高频信号作为分析对象进一步提取退化特征，将提取的特征输入至SVM中进行训练和测试，最终根据SVM的输出结果验证所提取退化特征的有效性。

图3 超声波电动机退化特征提取步骤

3.2 超声波电动机孤极信号的采集

本文通过超声波电动机试验台实现孤极信号的采集，试验平台如图4所示。整个试验平台由超声波电动机、电机驱动器、制动器、张力控制器、扭矩传感器、转速传感器、数据采集卡、底座和计算机等部件构成。超声波电动机型号选取目前应用较广泛的GTUSM-60行波型旋转超声波电动机，电机的工作频率为40.65kHz，其外观图如图5所示，图5中所标明的管脚为孤极，它能够实时反映定子的振动状态。

图4 超声波电动机试验台

图5 GTUSM-60超声波电动机

(a) 正常电机

(b) 轻度退化电机

(c) 严重退化电机

(d) 失效电机

由于电机的工作频率在高频段，数据采集卡采用TiePie的HandyscopeHS4高速数据采集卡。为获得较为真实的孤极信号数据，本文采用加大电压和加大负载的方式加速压电陶瓷片的开裂，不同退化程度的电机采取不同开裂程度的压电陶瓷片代替正常的压电陶瓷片的方式模拟，试验所用的压电陶瓷片如图6所示。采集的4种退化状态(将正常状态看作一种特殊的退化状态)的电机孤极信号各50组，每组采样点数为10240，数据采样频率为500kHz，试验过程中设置试验台的张力控制器的输出 为0.2A，采集到的孤极信号如图7所示。

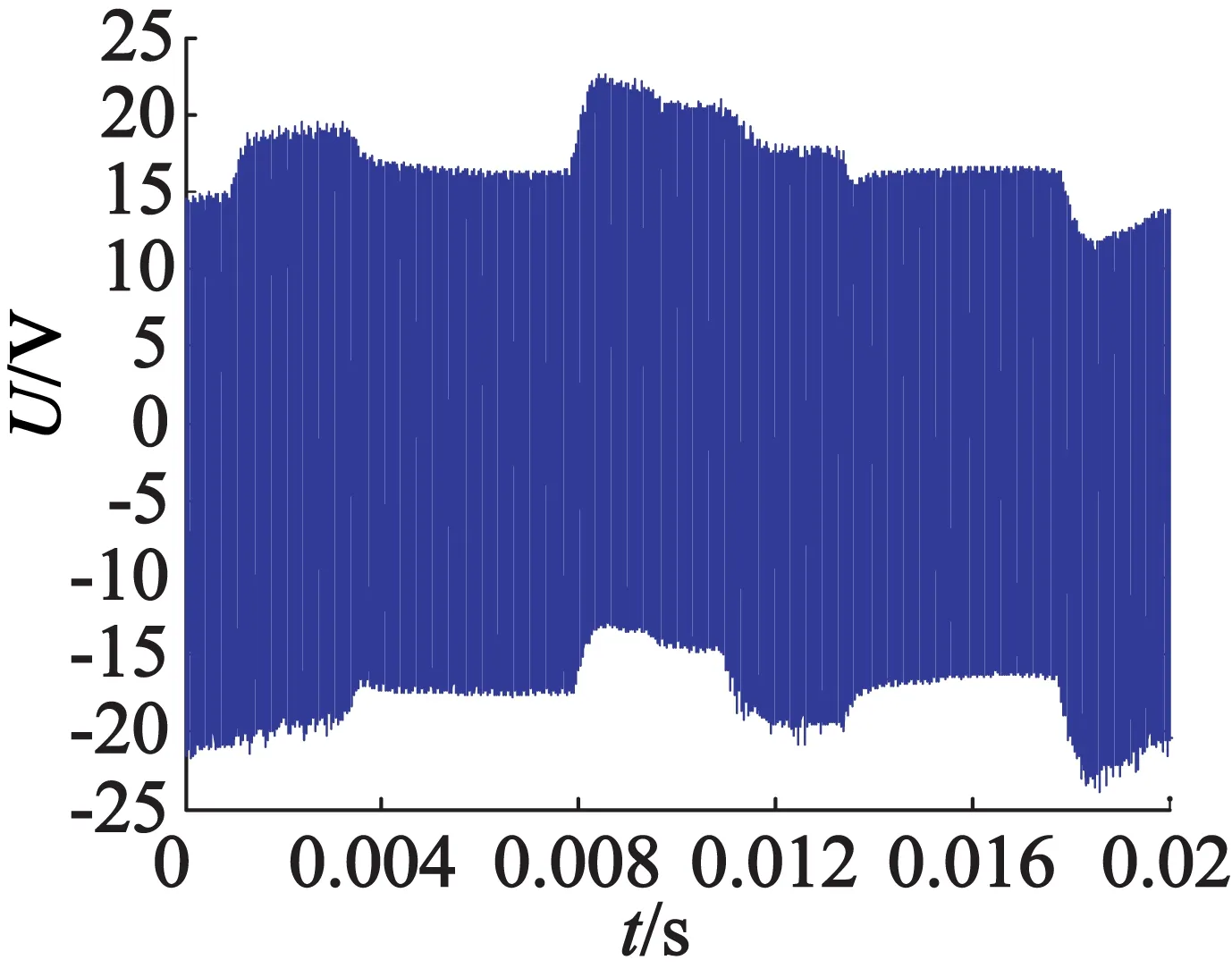
(a) 正常状态

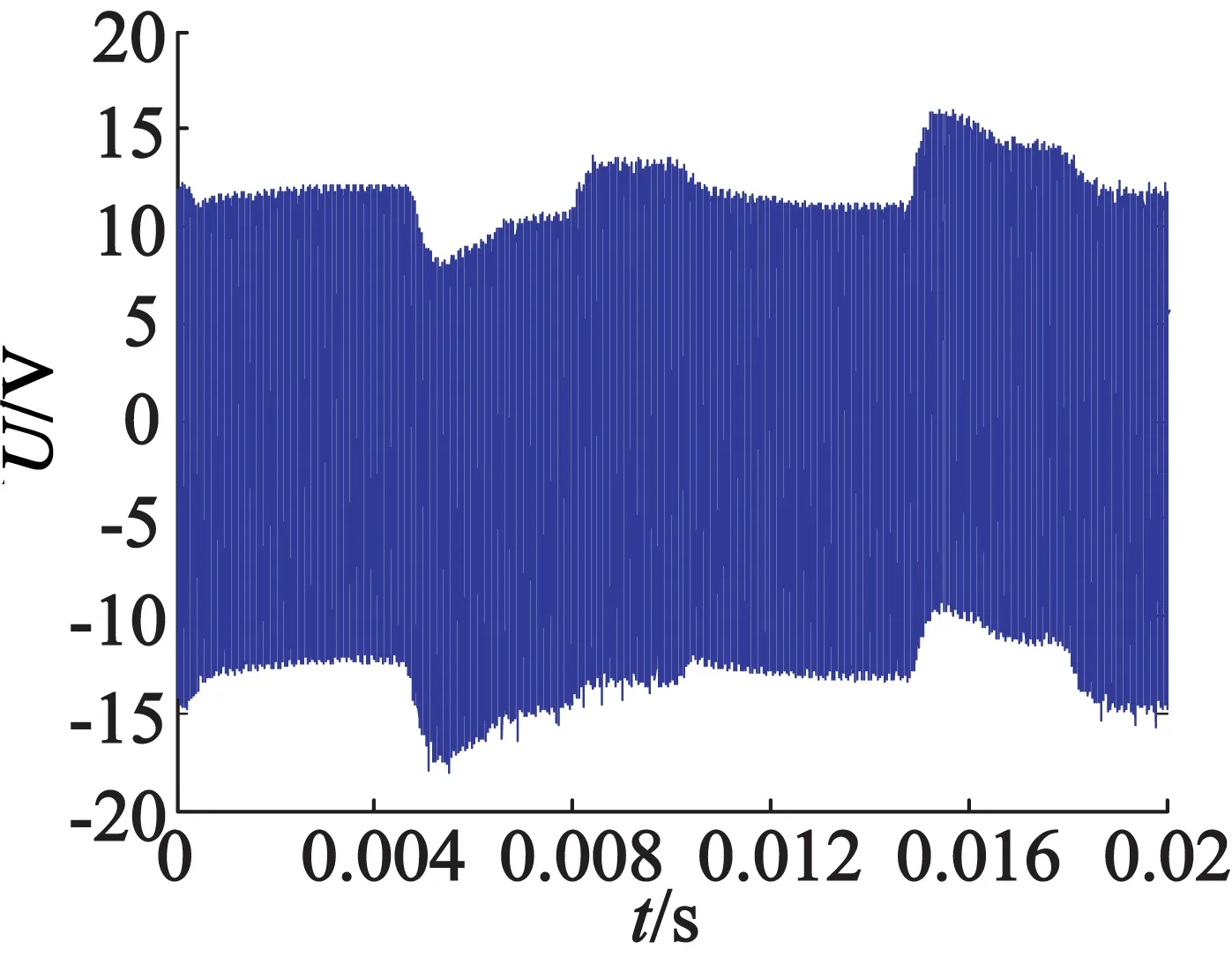
(b) 轻度退化

(c) 严重退化

(d) 失效状态

3.3 退化特征提取

3.3.1VMD信号处理

在退化特征提取之前必须通过VMD处理方法确定反映定子振动状态的高频信号，VMD的分解层数k设定为3，孤极信号的VMD分解如图8所示。从图8中可以看出，IMF2分量和IMF3分量为高频成分，IMF2分量频率为电机工作频率，并且IMF3分量频率为IMF2分量的倍频，而IMF1分量为低频成分。通过VMD处理找出信号反映定子振动状态的成分，为后续特征提取奠定良好基础。

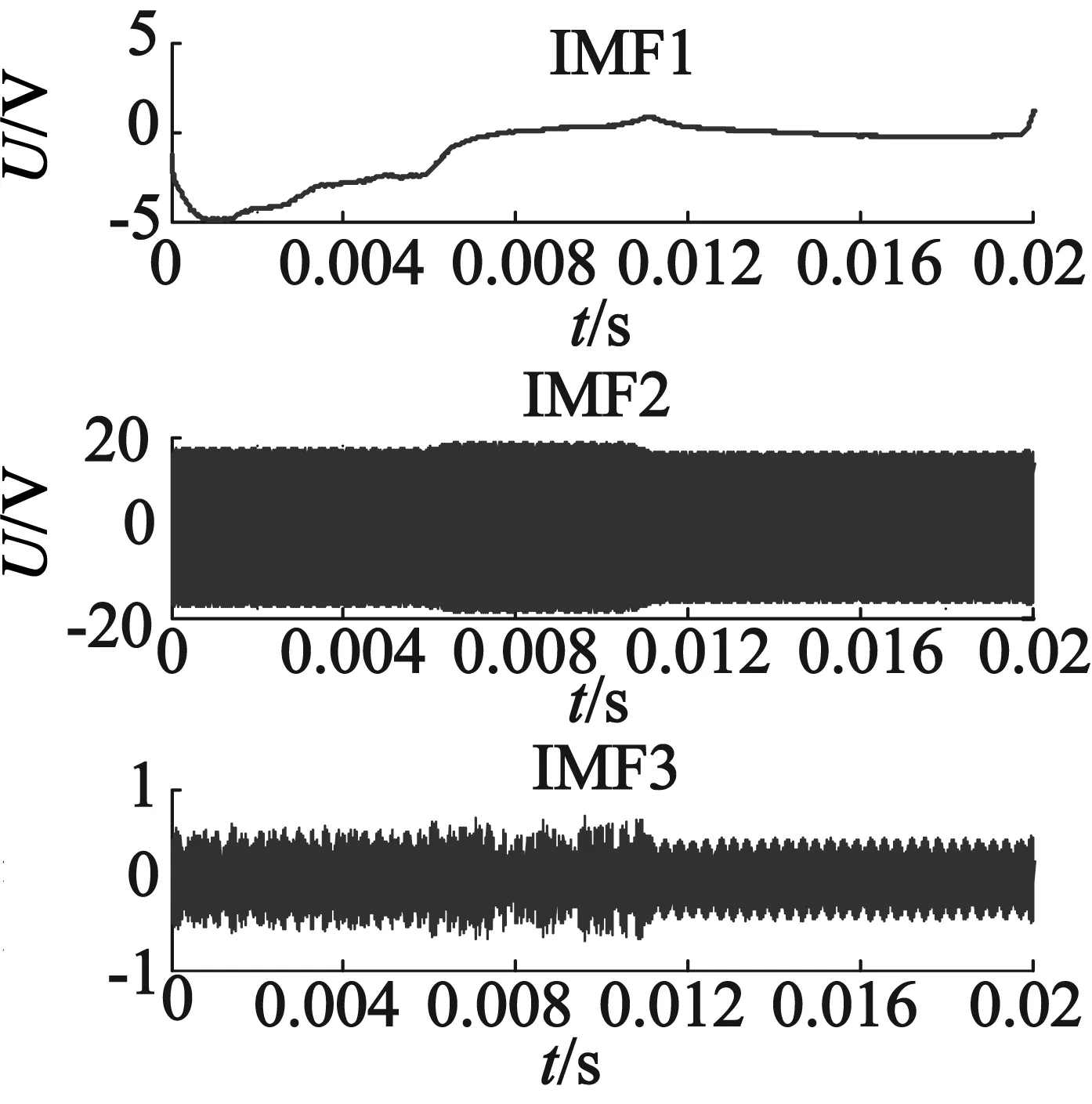
(a) 时域

(b) 频域

3.3.2 退化特征提取

超声波电动机退化程度的不断加深会导致定子结构的振动力度和能量出现下降的趋势，高频信号的均方根值(以下简称RMS)和能量能够反映定子的振动强度和能量，因此时域特征中的RMS和能量应该能够反映超声波电动机的退化程度不断加深的趋势。弧极信号方差能够表征偏离平均值的大小，压电陶瓷的开裂通常都是在某一处出现裂纹，该处的质点在高频振动时会受到严重影响，从而偏离平均值，因此方差也能够反映超声波电动机的退化状态。将2个高频成分分量IMF2和IMF3重组成高频信号，计算高频信号的RMS、能量和方差；在频域分析中，工作频率及其倍频处的幅值能够表明在此频率分量的信号强弱，而压电陶瓷的不同程度开裂导致定子弹性体上质点以40.65kHz超声振动出现不同程度的减弱，因此也可将其作为退化特征。通过任选10组数据分析，以验证所提出的退化特征表征超声波电动机退化状态的特性，它们的波形如图9所示。

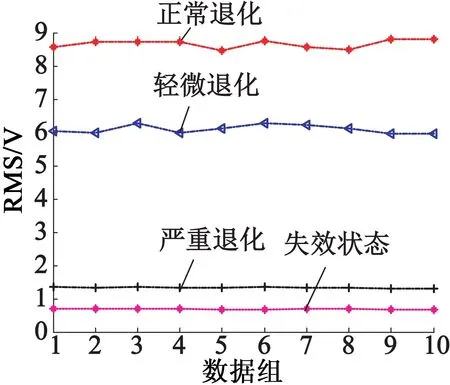
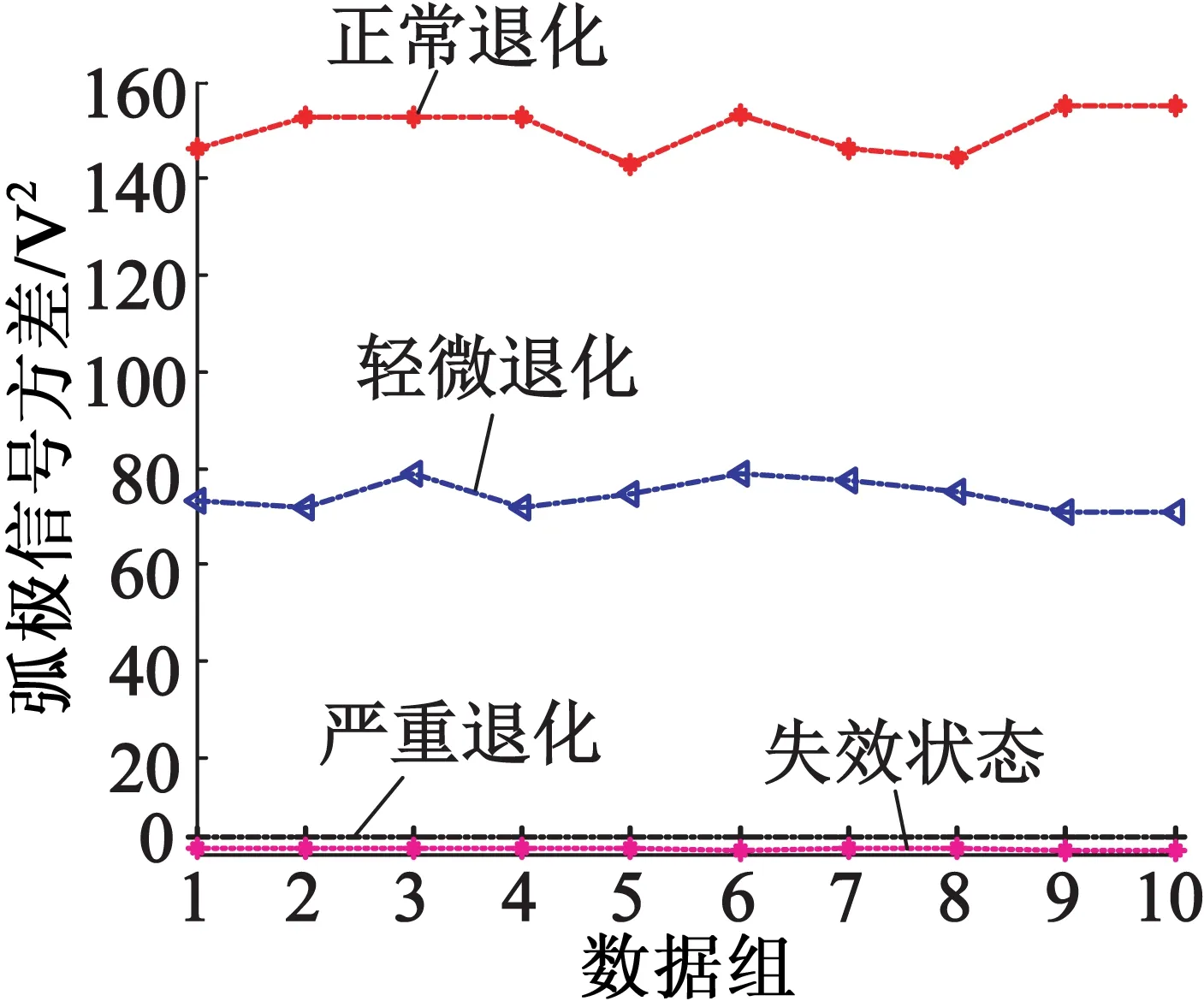
(a) 时域特征的RMS，能量和方差

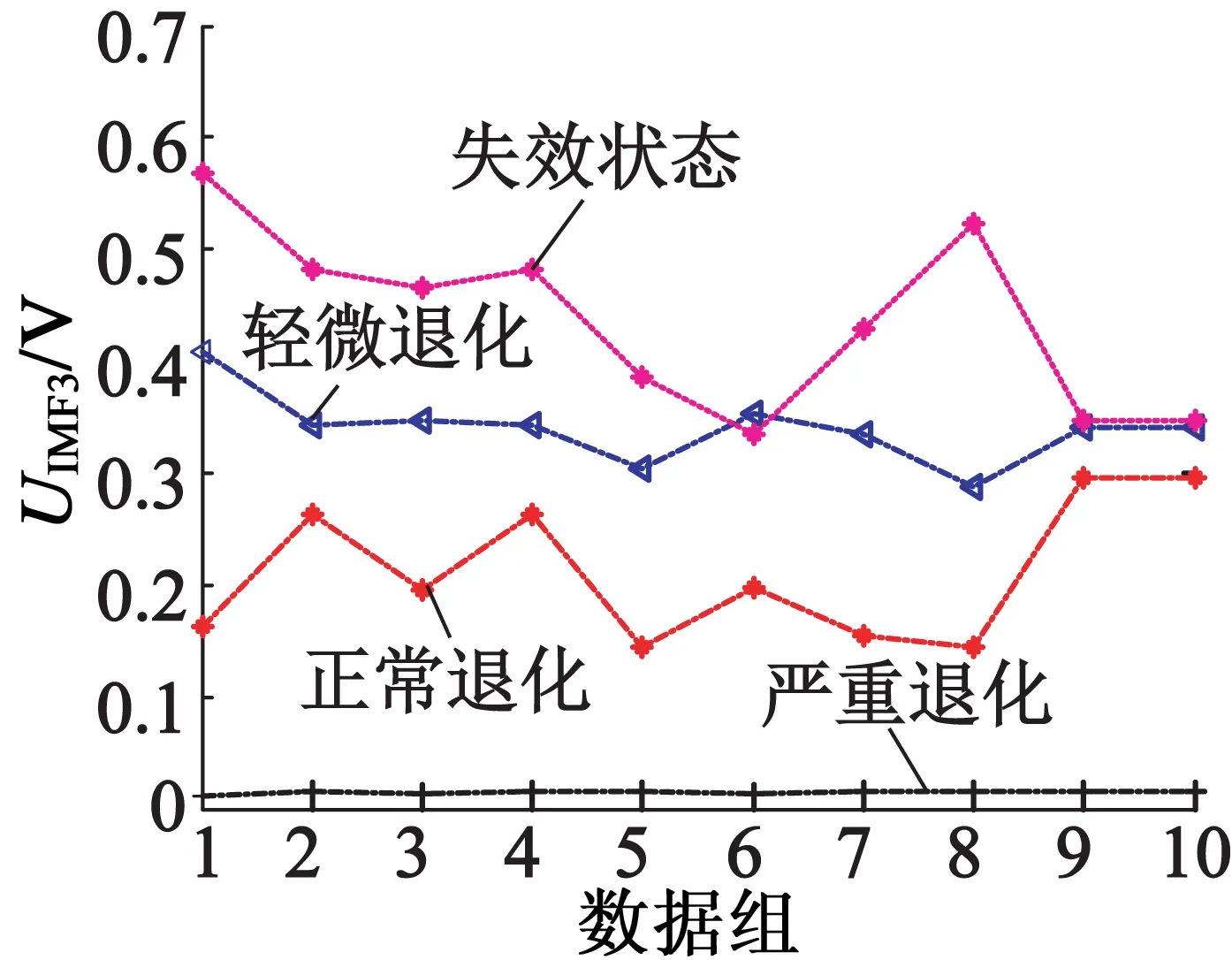
(b) 频域特征

4 验证提取退化特征的有效性

4.1 SVM

贝尔实验室的Vapnik教授最早提出SVM理论[16]，该理论具有很强的泛化能力，并已广泛应用于机械、电力和医学等多个领域。SVM是基于统计理论和风险最小准则的一种机器学习算法，其主要通过核函数将原始特征映射到某一高维空间中，在此高维空间寻求一个使得类与类间隔最大保证分离正确率最高的最佳分类面。在实现分类算法前必须将训练样本代入SVM模型中进行训练，经过训练后的SVM模型具有较好的识别能力。因此，合理的SVM模型的训练是SVM输出精准度的前提。图10为SVM的工作过程。

图10 SVM工作过程

4.2 退化状态识别

退化状态识别能力是评价退化特征性能的一个主要方面，主要反映了特征对不同退化阶段的区分能力。退化状态识别从本质上看作是一种模式识别问题，可以将不同的退化状态看作不同的模式，基于提取的退化特征并通过一定的识别方法对设备进行退化状态识别[17]。本文采用SVM的方法对超声波电动机进行退化状态识别。每种退化状态的超声波电动机各取50组样本(20组训练样本，30组测试样本)，采用训练建立的SVM模型对测试特征集进行退化状态识别。

SVM核函数中的径向基核函数对于任何类型的问题都不会出现太大偏差，并且径向基核函数：

仅有一个参数σ，参数确定数量相对较少[18]，因此本文选取径向基核函数作为SVM的核函数。不同的数据类型寻找最优参数也是SVM模型建立的难点问题之一。经典传统算法包括枚举法和网格搜索算法，这两类算法计算过于复杂，需要消耗的计算时间太长，于是很多学者开始将智能优化算法引入SVM模型参数寻优中，遗传算法以及粒子群算法开始逐渐应用于SVM的参数优化中[19]。遗传算法容易陷入局部最优，因此本文选择粒子群算法来确定惩罚参数c和核函数参数g，将粒子种群数设定为20，迭代终止数设为100，设c∈(0.1,100)，g∈(0.01,1000)，粒子在二维空间中寻找最佳组合，最佳参数为c=3.75，g=0.125，寻优迭代适应度曲线如图11所示(由于在21代已经找到最优结果，在此只罗列前30代适应度曲线)。

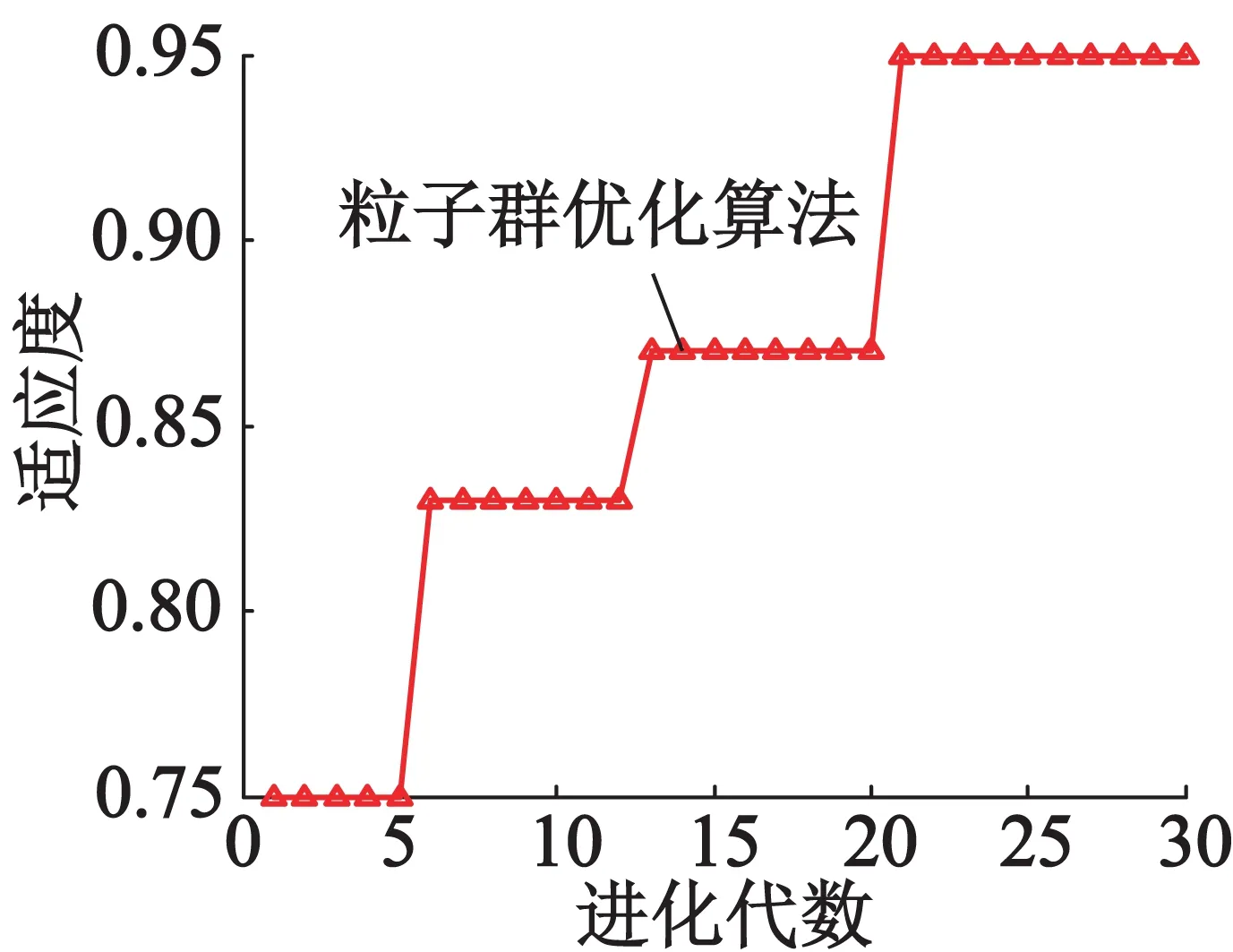
图11 粒子群算法适应度曲线

将提取的退化特征输入至参数设置好的SVM中，得到检测结果如图12所示，测试样本标签1,2,3,4分别代表4种退化状态(1代表正常状态)，最终的识别准确度为95.83%，仅有5组数据将轻微退化状态错误识别为正常状态，识别时间为1.981 550s(运行平台为MATLABR2011b，计算机主要配置为：CPUIntel(R)Core(TM)i5-4590 3.30GHz,memory4G)，可以看出，本文的退化特征提取方法基本能够准确地反映不同的退化状态，从而说明退化特征的有效性和准确性。同时提取的退化特征在保证识别准确率的基础上，识别时间较短，保证了识别结果的准确性和实时性。

图12 退化状态识别结果

5 结 语

VMD信号处理方法能够有效地将孤极信号中反映定子高频振动的成分分解出来。

超声波电动机孤极信号能够反映定子的振动状态，其高频成分蕴含丰富的状态信息，本文研究的退化特征提取方法能够较好地反映超声波电动机的退化状态，并为保障电机的安全运转提供一定的参考意义。

通过分析测量的信号发现，不同退化状态的超声波电动机电流信号也会发生一定的变化，未来可以通过监测多种信号进行信息融合的方式，进一步提取出更加全面反映超声波电动机退化状态的退化特征。