数形结合思想在高中数学教学中的应用

张立娟

（吉林省榆树市第一高级中学，吉林 榆树）

数学学科的一个本质特征就是数形结合，其依据数的结构特征，构建与之适应的几何图形，同时借助图形的特征与规律解决数的问题；或者将图形信息转化为代数信息，从而将图形问题转化为数量关系进行讨论。高中数学教学中数形结合思想的合理应用，综合了形象直观、便于理解的几何图形和程序化、一般性、可操作性的代数方法，能够帮助学生更好地学习、理解相关数学知识，从而不断提升数学能力水平。

一、数形结合思想的内涵与应用原则

1.涵义

数和形是高中数学中的两个非常重要的元素，数就是指数量关系，形就是指空间图像。数形结合就是数量关系和几何图像之间转化，有机结合抽象与形象思维，从而利用形象化的图像解决抽象化的问题，实现高中数学学习的飞跃，并有效提升学生的解题能力。

2.应用原则

以几何图形分析代数抽象性与以代数语言避免几何直观约束性的双向性原则，充分发挥数形结合的优势；数形转换过程中，代数性质与几何性质应保持等价性原则；高中数学的实际教学过程中，教师应坚持以知识为载体，恰当应用数形结合思想，坚持渗透性原则；此外，数形结合思想在高中数学教学中的应用应严格遵循学生参与的原则，教师应为学生提供合理的学习时机、素材与平台，为其营造和谐的学习氛围，引导其参与知识的发生与发展过程，增强高中数学教学效果。

二、数形结合思想在高中数学教学中的应用

在应用数形结合思想分析、解决高中数学问题的过程中，首先应引导学生明白一些概念、运算的结合意义、曲线的代数特征等；同时，参数设置应恰当、合理应用，正确建立关系，做好转化；此外，参数的取值范围应正确设定，“数”与“形”应很好地结合，便于求解。

1.注重数形之间的转换，将抽象的数学知识变得具体化

相比于数学语言，图形更具强大的形象性、直观性，所以，高中数学教师可合理借助数形结合思想，将抽象的代数难题转换成图形的形式，从而吸引学生的注意力，充分调动其思维，帮助其获取明确的解题思路，不断提升解题能力。

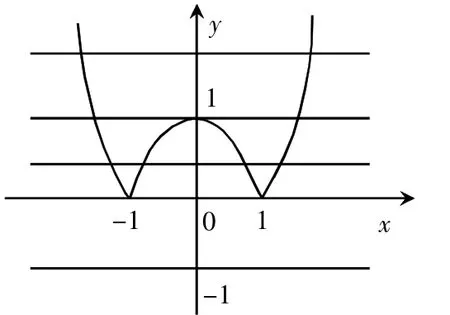
图1

当k值＜-1时，两个函数不相交，所以原方程无解；当k值=-1时，函数在图中显示两个交点，所以原方程有2个解；当k值处于-1～0之间时，函数在图中显现四个交点，原方程有4个解；当k=0时，函数在图中显现三个交点，原方程有3个解；k值＞0时，函数在图中显现两个交点，原方程有2个解。

应用数形结合思想解决函数交点个数或求解方程等问题，能够借助直观的图形锻炼学生的观察能力，有利于启发学生的解题思路，进而拓展其思维空间，提升其数学解题与思考的能力。

2.“数”与“形”的结合在高中数学教学中的应用

事实上，在高中数学的教学过程中，无论是以“数”解题还是以“形”解题都是有一定缺陷的，但二者又是相辅相成的。因此，高数的很多问题都需要充分结合数、形的优势，共同运用以解决数学问题。如：一些静态函数问题可以借助坐标系-图像进行动态表达与阐述，图像能够弥补函数形象性、直观性不足的缺点，如直线图、圆锥曲线图形等能够对一些代数的变化进行充分表达；而精准计算的函数解析式又增强了图像的精准性。二者的有机结合，能够有效解决高中数学中的一次函数、二次函数、三角函数等问题。

例如：圆（x-2）2+y2=3上存在一个任意点 M（x，y），求取（x-y）的最小值与最大值。在解析的过程中，就可以假设x-y=b，将直线方程转换为y=x-b。当圆与直线相切时，即为直线y=x-b在y轴的截距，如图所示。这时，b1为最小值，b2为最大值。

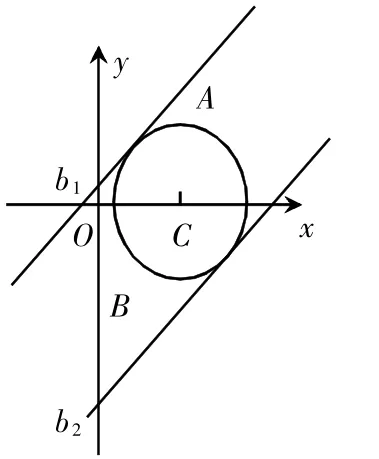
图2

综上所述，作为一门具有较强理论性与逻辑性的学科，高中数学对学生来说具有较大的难度。因此，教师应合理渗透数形结合思想，引导学生有机结合数与形，更好地解决相关数学问题，不断提升数学思维水平与能力。