为发展学生的思维而教
张秀花
【摘要】数学是思维的体操,“为发展思维而教”是数学课堂教学的必然要求,教师要以生为本,根据学生的思维发展规律、认知基础来展开课堂教学,让学生充分经历观察、猜想、操作、实验、推理、交流、应用的活动过程,把培养学生的思维能力贯穿在每一个教学环节中。从“激活,让思维启航放飞”入手,精心“设计链接,给思维搭建阶梯”,让学生“聚焦问题,把思维引入知识核心”,在真实的数学活动中,引导学生思维的主动参与,有效发展学生的数学思维能力。
【关键词】课堂教学;数学思维;核心素养
数学是思维的体操,对数学老师而言,“为发展思维而教”是数学课堂教学的必然要求(郑毓信)。宫振胜教授在题为《谈核心素养最应该聚焦的是思维素养》一文中明确提出“谈核心素养最应该聚焦的是思维素养”。当下的数学课堂,需要更加关注数学核心素养,而落实数学核心素养的一个核心是数学思维,我们要把培养学生的思维能力贯穿在数学课堂的每一个环节中,以学生为本,依据学生的认知基础、思维规律、学习心理设计并展开教学,引发学生火热的思考,积极引领学生进行高质优效的数学思维,在数学课堂真正践行“为思维素养而教”!
一、激活:让思维启航放飞
维果茨基的最近发展理论告诉我们,学生总是带着一定的数学知识经验与生活经验走进课堂的。课堂教学中,教师要重视以学生的认知发展水平和已有的經验为基础,把握好学生的认知起点,寻找合适的起点让学生真正展开数学学习,唤起探索知识的欲求,让学生的思维起航放飞。
如一位老师执教《用数对确定位置》,课始,播放江苏卫视《最强大脑》的片头) 创设“最强大脑”的视频情境……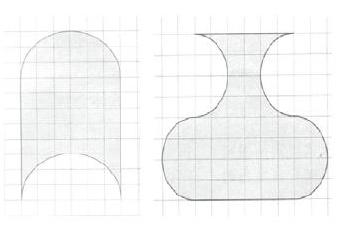
师:请你说说武亦姝在图中的位置?
预设三个同学不同的说法,请同学到前面边数边说是怎么数。
师:同学们,同一个位置为什么说法却不一样呢?
生:观察的角度不同。
师:是的,怎样才能统一、正确地确定武亦姝的位置呢?今天这节课我们就一起来研究《确定位置》。
师:习惯上把竖排的称为列,横排的称为行。认识“确定第几列要从左往右数,确定第几行要从前往后数”的规定。
学生试着用第几列第几行来描述武亦姝的位置。抽象成圆圈图,让学生找武亦姝的位置。试着再练习几个圆点的位置描述。
老师适时引导学生回顾学习过程,让学生感受到“标准统一”了,交流起来就准确了。接着让学生试着创造数对,并用数对表示点的位置。如以“第4列第3行”为例,该怎样简写呢?学生试着创造一些简洁的写法。比较几种不同写法之间的相同部分。认识到两个数的重要性,以及两个数之间怎样区分。
老师讲解数对的写法以及读法,学生试着用数对表示其他两个位置,再让学生根据数对找点的位置:“给你数对,你能找出它所表示的圆点的位置吗?”学生自己在作业纸上完成。比较(4,1)和(1,4)的异同,认识位置和数对是一一对应的。
上述教学过程中,这位老师引导学生不经意间沉浸在“最强大脑”的头脑风暴中,使学生初步认识确定位置的重要性。学生在具体情境中认识列、行的含义,知道确定第几列、第几行的规定,初步理解数对的含义,会用数对表示具体情境中物体的位置。学生经历由具体的座位图抽象成用列、行表示的平面图的过程,提高了抽象思维能力。
二、链接:给思维搭建阶梯
古人云:“不闻不若闻之,闻之不若见之,见之不若知之,知之不若行之;学至于行之而止矣。”《课程标准(2011年版)》也明确提出:学生学习应当是一个生动活泼的、主动的和富有个性的过程。学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。因此,在教学中,教师应该努力为学生搭建探究、发现的学习平台,让学生有充分的时间进行操作实践,在数学知识的抽象性与学生思维的形象性之间做个链接,引导学生在直观的实践活动中自主探索、思考、感悟,积累丰富的数学活动经验,从而使学生经历和体验知识创生与发展的过程。
如一位老师执教《解决问题的策略——转化》,新课伊始,教者呈现了一个直观性和操作性极强的素材图“哪个图形的面积大?”
学生先进行观察思考,再通过教师提供的学具图操作实践,通过平移和旋转把这两个图形转化为一个长方形。“一千个读者就有一千个哈姆雷特”,基于这样典型而具有直观性的图形,在操作实践的过程中,学生迸发了不同的灵感,产生了不同的转化方法。
学生对图一有如下方法:
生1:把上面的半圆剪切向下平移8格填补到下面空白的半圆处,就拼成了一个长方形。
生2:把下面的图形剪切向上平移8格填补到上面的空白处,就拼成了一个长方形。
生3:也可以从中间剪切向下平移6格,也拼成了一个长方形。
学生对图二有如下方法:
生1:把下面2个半圆分别围绕一点向上旋转180度,拼成一个长方形。
生2:把上面突出的部分平均分别围绕一点向下旋转180度,也拼成一个长方形。
生3:把图形下面突出的半圆向里折,再把图形从中间横着对折,也拼成了一个长方形,再用拼出的长方形面积乘2,就得出原来图形的面积。
在这里,教者通过让学生操作实践,把课堂还给学生,把思维和创造还给学生。一石激起千层浪,当第一个学生寻找到转化的方法时,唤醒了学生群体原有认知中的“转化”体验,个个跃跃欲试,纷纷投入到探究中。因此,真实的动手操作,能指向思维的核心区间,着眼于思路的打开、思维的碰撞,能在数学知识的抽象性和学生思维的形象性之间架起一座桥梁。学生在真实的操作活动中展开火热的思考,给学生的思维搭建了阶梯,有效发展了学生的数学思维能力。
三、聚焦:把思维引入核心
认知块、问题串、思维场,以问题为中心引领教学,以思维为核心促进发展,关注核心知识,发展思维能力。为此,数学教学应该紧扣本质挖掘题材,精心组织有价值的教学活动。引导学生综合运用已学到的知识进行分析和思考,有效地解决生活中的实际问题,既能巩固所学知识,又能培养学生灵活运用知识解决问题的能力,使他们的认识更加清晰、思维更加深入,同时也使师生间的活动向更高的水平推进。
如一位老师执教“多边形的内角和”时,在课尾,提出一些有意义且富有挑战性的问题,让学有余力的学生放飞思维,向思维的更深处漫溯。
师:通过刚才的探索,我们知道了多边形的内角和算法。多边形在生活中有着广泛的运用,掌握了多边形的特点,可以解决生活中的一些实际问题。欣赏一下,这些多边形的砖铺在地面、贴在墙上,感觉如何?
生:这些砖铺起来,很好看,很美观。
师:这些瓷砖、地砖是特殊的多边形,一般是正三角形、正方形、长方形、正六边形的规则图形。一块挨着一块地铺,没有空隙,这叫密铺。但是,正五边形的砖却不常见,你知道为什么吗?(图1)
生:用正五边形的砖来铺,还缺少一小块,不能密铺。
师:想一想,没有铺满的这儿,这个夹角是多少度?能用刚才得到的规律来解决吗?(没有学生举手)
看来这个问题有点难度,那么就请小组同学一起思考、讨论。(图2)(学生分组讨论)
师:讨论有结果了吗?现在谁来把想法说给大家听听?(指名汇报交流)
生1:从图中间来看,这个要求的角和另外3个角形成一个周角,因为这3个角分别是3个五边形的其中一个角,所以先算出五边形各角的度数。五边形的内角和是180°×(5-2)=540°,它每个角度数就是540°÷5=108°,这个夹角是360°-108°×3=36°。(图3)
师:思路非常清晰。还有其他想法吗?
生2:空白的地方可以看成是一個等腰三角形,只要算出底角度数,就能算出顶角度数。
师:很不错的补缺法!请你继续说下去。
生2:五边形的一个角和这个等腰三角形的底角合起来是平角,先算出五边形一个内角的度数180°×(5-2)=540°,540°÷5=108,再算一个底角度数180°-108°=72°,然后算顶角的度数180°-72°×2=36°。(图4)
师:同学们真聪明。能综合运用学到的知识,灵活而深入地思考,解决了实际问题。用正五边形和等腰三角形,依次重复混合起来铺,也会形成漂亮的图案,只是施工过程较为复杂,可能会费时费料。(图5)
师:关于多边形的知识,你还想了解什么呢?
……
上述案例中,教者注意问题聚焦,把学生思维引入核心知识,课尾设计很有层次、有梯度,能引发了学生的深度思考、多角度思考。学生对平面图形的知识进行灵活运用的过程中,思维不断接受新的挑战,训练数学思维的灵活性和深刻性,有效提升了学生的思维品质。
总之,数学育人的核心是发展学生的理性思维,基于核心素养的数学课堂教学,需要紧紧抓住“为发展思维而教”这个核心,“基于儿童,研究儿童,发展儿童”;深入研究学生的思维特点和认知规律,紧贴着学生的思维现实展开教学活动。恩格斯说:“思维是地球上最美丽的花朵。”让思维之花在数学课堂绽放异彩!

