基于量纲分析的爆炸冲击波作用后钢化玻璃碎片质量分布规律研究

钟巍， 田宙， 寿列枫， 李伟昌， 何增， 浦锡锋， 王仲琦

(1.西北核技术研究所， 陕西 西安 710024； 2.北京大学 数学科学学院， 北京 100871；3.北京理工大学 爆炸科学与技术国家重点实验室， 北京 100081)

0 引言

随着暴恐袭击的频发以及燃气爆炸等意外事故的日益增多，建筑玻璃在受到爆炸冲击作用后的破坏性能成为近年来国内外的研究热点。Linz等[1]利用数值模拟研究了夹层玻璃在受到冲击波作用后的层裂性质，能够为带夹层玻璃建筑结构的建模和设计提供一种新的方法。Linz等[2]对夹层玻璃受到冲击荷载作用后的破碎行为提出了一个解析解，从而可以为风险评估工程师和带夹层玻璃幕墙建筑的设计者提供高效的方法。Zhu等[3]建立了由小块夹层玻璃组合而成的面板或门窗的数值模型，通过数值模拟研究了受到爆炸冲击作用后的动态响应行为。Chen等[4]利用有限元方法模拟了带聚乙烯醇缩丁醛(PVB)夹层玻璃的冲击破坏效应，通过数值模拟得到了玻璃在破坏过程中应力波的传播特征，进而给出了玻璃受到爆炸冲击作用后的破坏机理。王书鹏[5]将有限元方法与薄板振动理论相结合，研究了建筑玻璃在爆炸冲击波作用下的破碎原因、破碎模式和碎片分布规律等。师燕超等[6]基于有限元显式动力学分析软件LS-DYNA提出了模拟爆炸荷载作用下玻璃裂纹产生的节点分离法，使用该方法对某现场爆炸试验中玻璃板的破碎进行了数值模拟，研究了爆炸荷载作用下建筑玻璃的破碎情况。陈海杭等[7]对建筑玻璃幕墙的抗爆性能进行了研究综述。

综上所述，大量学者在爆炸冲击波对建筑玻璃破坏效应方面卓有成效的研究成果可以为风险评估和建筑设计等提供很好的参考。然而，已有的绝大部分研究都集中在玻璃破坏模式、破坏状态本身，极少有关于玻璃碎片对人员造成伤害的研究。事实上，建筑玻璃在受到冲击波作用破坏后会产生大量飞散的玻璃碎片，将对建筑内人员造成以割裂、擦伤等为主的伤害[8-9]。碎片对人员造成伤害的程度主要取决于碎片的尺寸(形状)、飞散速度和质量等。在已公开发表的文献中没有发现关于玻璃碎片质量分布规律预测公式方面的研究结果。因此，针对开展的冲击波毁伤钢化玻璃效应试验，在本文中将给出玻璃碎片质量分布规律的研究结果。考虑到篇幅等多种因素的限制，玻璃碎片的尺寸、碎片飞散速度等的研究结果将另文给出。本文首先对试验中收集的玻璃碎片质量分布数据进行统计和整理，然后利用量纲分析推导出玻璃碎片质量与飞散距离的无量纲函数关系式，最后结合试验结果和无量纲函数关系式，给出预测玻璃碎片质量随不同飞散距离分布的经验公式，并通过与试验结果的对比和相关系数及决定系数的计算分析验证预测公式的合理性。

1 钢化玻璃冲击波毁伤效应试验概况

试验采用按制药标准熔铸的梯恩梯(TNT)裸药柱，炸药密度为1 640 kg/m3，分为5 kg和10 kg两种质量。为了确保钢化玻璃的正中心与炸药的爆心位于同一水平面上，将TNT炸药自由放置在一个塑料方凳上面，并确保药柱中心与钢化玻璃正中心距离地面的高度一致，试验现场布局如图1所示。图1中R0为到爆心的距离。

试验中使用的钢化玻璃均按照建筑标准JGJ102—2003玻璃幕墙工程技术规范[10]加工制造，长和宽分别为1.6 m、1.2 m，玻璃表面压应力α=69 MPa(按钢化玻璃进一步的细分标准，本研究采用的玻璃属于半钢化玻璃：24 MPa≤α≤69 MPa)。3轮次试验所使用的TNT炸药质量及玻璃厚度如表1所示。

2 玻璃碎片质量分布试验统计结果

为了研究钢化玻璃受到爆炸冲击波作用后可能造成的次级毁伤效应，在试验现场开展了玻璃碎片收集与记录工作，如图2所示。参照文献[11]中的碎片收集方法以及文献[12]“弹体破碎性试验”中“试验结果整理和评定”的标准，本试验中玻璃碎片的收集与记录方法为：1)爆炸结束后，如果玻璃破碎，则进行碎片统计；2)现场观察玻璃碎片的分布特点后，将玻璃碎片分布的区域划分为若干区间，对每个区间内的玻璃碎片尺寸和质量进行人工统计；3)在统计时对于尺寸过小的碎片(指最大长度小于0.3 cm的碎片)不作统计；4)为了提高统计速率，现场统计每个区间的碎片时，先统计尺寸明显较大(通常分布不均匀)的碎片，对于剩下的分布比较均匀的碎片，先将区间分成若干等份，只统计其中1等份的碎片情况，然后乘以等份数得到整个区间的碎片情况。尽管上述统计方法会存在一定的试验误差，但分析表明误差在工程上可以接受的范围以内。例如，对于试验中10 mm厚的玻璃，玻璃密度为2.50 g/cm3，则其总质量为48 kg，试验中5发试验回收到碎片平均总质量为37.75 kg(见表2和表3)，平均回收率达到78.6%. 此处给出两点补充说明：1)考虑到钢化玻璃相对钢质弹体或铸铁弹体而言在破碎时会产生更多的接近粉末的“碎片”，在试验现场很难进行统计，因此，虽然本研究中碎片回收率无法达到文献[12]中90%的比例，但对比文献[11]中的结果，可以认为此时75%以上的回收率在工程估算中是有效的；2)本文研究只在第1轮试验中对被冲击波破坏的钢化玻璃进行了玻璃碎片质量分布称重统计，因为第2轮试验时试验场地紧张，开展试验的时间受到限制，故没有进行碎片统计工作，第3轮试验采用的全部是带PVB夹层的玻璃，玻璃破碎后不产生碎片飞散的问题，无需进行碎片统计。

表1 TNT炸药质量和玻璃厚度

如图3所示，取玻璃安装平面作为参考平面，以参考平面为坐标原点建立坐标系，参考平面到爆点一侧用x轴的负半轴表示，相反的一侧用x轴的正半轴表示。记碎片分布区域中点坐标为R(简称为飞散距离)，并在后续分析中用该中点坐标来表示对应的碎片区域。

根据碎片质量现场称量结果，整理得到了各发次试验碎片质量在不同分布区域的统计数据，统计数据见表2、表3和表4，表中只给出了玻璃破坏时对应的试验发次。

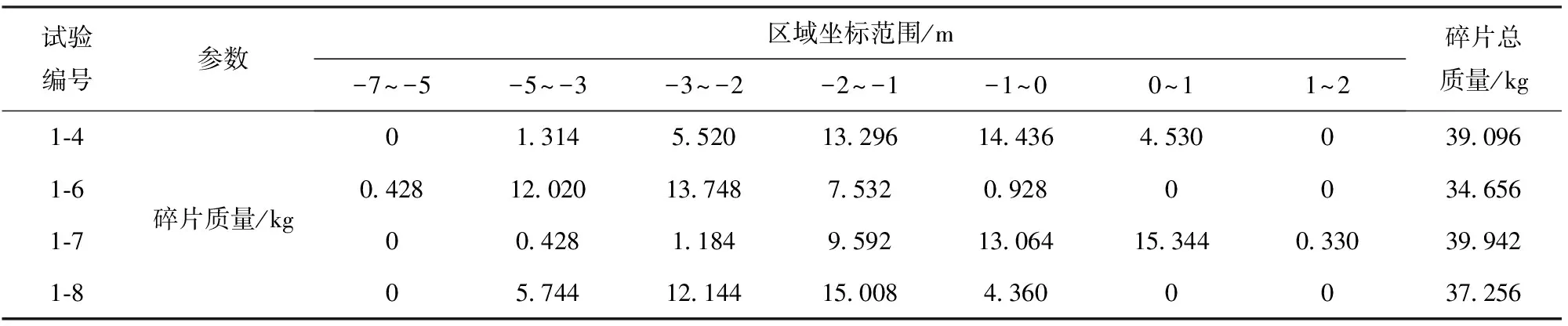
表2 10 mm厚钢化玻璃碎片质量分布情况1

表3 10 mm厚钢化玻璃碎片质量分布情况2

表4 6 mm厚钢化玻璃碎片质量分布情况

根据上述试验统计结果，作出碎片质量关于飞散距离的分布图，以1-4和1-10试验为例，结果分别如图4和图5所示。由图4和图5可见，碎片质量与飞散距离R的关系整体上近似呈正态分布。以此观察结果为基础，利用量纲分析方法，下一节将推导出碎片质量随不同飞散距离分布规律的半经验预测公式。

3 玻璃碎片质量分布规律预测公式

3.1 量纲分析

“不同区域(用区域中点R表示)内玻璃碎片质量m的分布”问题中涉及的物理量及单位与量纲如表5所示，本文后续推导得到的无量纲化数学公式都是在表5所示量纲和单位条件下得到的，在应用时必须先确保公式中相关的物理量量纲和单位与表5中相符。由表5可知，存在函数关系式

m=f(R;Q,ρe,Ee,γe,R0;pa,ρa,γa;
dg,ρg,E,ν,Y,S,L,W).

(1)

显然，上述物理量的基本量纲为L、M、T，不妨取Q、ρe、Ee作为基本量，根据量纲分析的基本原理和Π定理[13]，对(1)式无量纲化后可得

(2)

表5 玻璃碎片质量分布问题中相关物理量及其单位和量纲

对于第1轮试验玻璃碎片质量分布规律问题，所使用的玻璃都是同一批次生产的，同样，采用的炸药也是同一批次熔铸而成，且同一轮试验空气条件可视为相同，故存在

(ρe,Ee,γe;pa,ρa,γa;ρg,E,ν)=const.

(3)

由于试验过程中没有测量玻璃的屈服强度Y和抗拉强度S，需要消去(2)式中包含这两个参量的项。本文采用的方法是将不同厚度的玻璃分开研究，于是对于同一种厚度的玻璃而言，Y和S可以视作不变的量，即有

(L,S)=const.

(4)

利用(3)式和(4)式，可将无量纲函数关系(2)式简化为

(5)

(5)式即为基于量纲分析得到的玻璃碎片质量分布的定性关系式。

上述处理主要是由于缺乏更全面的试验数据而采用的简化策略，如果在类似的研究工作中能够测量获得更全面的试验数据，包括不同轮次试验玻璃、炸药和空气的参数等，则可以不进行上述简化和忽略相关因素的步骤，直接将(2)式作为玻璃碎片质量分布的定性关系式，按照本文接下来提供的方法和思路开展类似的分析研究，得到更准确全面的玻璃碎片质量分布规律预测公式。本文在有限的条件下，旨在提供一种研究的方法与思路，并在满足限制条件的情况下验证该方法和思路的合理性和可行性。

3.2 半经验预测公式的表达形式

如第2节所述，观察试验统计可知碎片质量与飞散距离关系近似呈正态分布，因此，参考正态分布函数的形式[14]，不妨假设上述函数的表达式为

(6)

式中：A1、A2、A3为待定系数；Rc为碎片质量最大值位置，其值根据试验数据统计结果确定。Rc还可以通过试验观察、理论估算或者直接假定为未知系数通过数据拟合得到，而且结果和试验值非常接近，但这样处理其物理意义不够明确。本文为了突出预测公式的物理意义，只对系数项进行拟合，有量纲意义的项不作拟合，直接采用试验数据统计结果；(6)式中其他参数的意义见表5.

由于在已开展的所有试验中，玻璃长度L是固定不变的，则(6)式可进一步简化为

(7)

对于每一发试验而言，(7)式中只有系数C1、C2

是需要确定的参数，m和R分别是因变量和自变量，其他参数均已知。根据试验统计得到的关于m和R的数据已在表2、表3和表4中给出，利用最小二乘法进行数据拟合，可以得到(7)式对应每一发试验的系数C1、C2，从而得到碎片质量分布关于飞散距离的函数表达式。对厚度相同的钢化玻璃，若每一发实验使用上述方法得到的系数C1、C2的值都很接近，则取其平均值代入(7)式中作为估算该厚度钢化玻璃碎片质量分布的半经验预测公式。

4 试验结果分析

4.1 10 mm厚钢化玻璃碎片质量分布的预测公式与结果分析

对于10 mm厚钢化玻璃，各发次试验对应(7)式中的基本参数如表6所示，表中破坏模式1和破坏模式2是指在试验中观察到的两种不同破坏模式：破坏模式1是指比例爆心距离比较大时，试验观察到此时玻璃碎片主要分布在玻璃安装位置到炸药放置点一侧，分析认为这是由于玻璃受到冲击波作用后由于负压、玻璃自身反弹与振动等原因造成的破坏，如图6所示；破坏模式2是指当比例爆心距离非常小时，试验观察到此时玻璃碎片主要分布在玻璃安装位置到炸药安置点方向相反的一侧，分析认为这是由于玻璃受到冲击波作用后在巨大的超压作用下直接被破坏，如图7所示。

表6 10 mm厚钢化玻璃碎片质量分布预测公式中的基本参数

将表6中的数据代入(7)式中，利用表2和表3中的试验结果得到碎片质量m和对应的碎片分布区域中点坐标R的数据，使用最小二乘问题中经典的Levenberg-Marquardt方法[15]进行数据拟合，得到各发次试验对应(7)式的系数C1和C2，进而确定各发次试验对应(7)式的确切表达式，结果如表7所示，曲线拟合效果评价参数如表8所示。根据表7中得到的预测表达式，作出碎片质量分布随分布区域中点坐标的函数曲线，将其与试验统计结果对比如图8～图12所示。

由表8可知，1-4、1-6和1-8试验对应的回归分析决定系数和相关系数都达到了0.9以上，均方差也相对要小，F统计量较大。因此，上述3发试验使用本文提出的半经验预测公式计算得到的碎片质量随分布区域中点坐标的分布规律与试验统计结果吻合得很好，如图8、图9和图11所示。

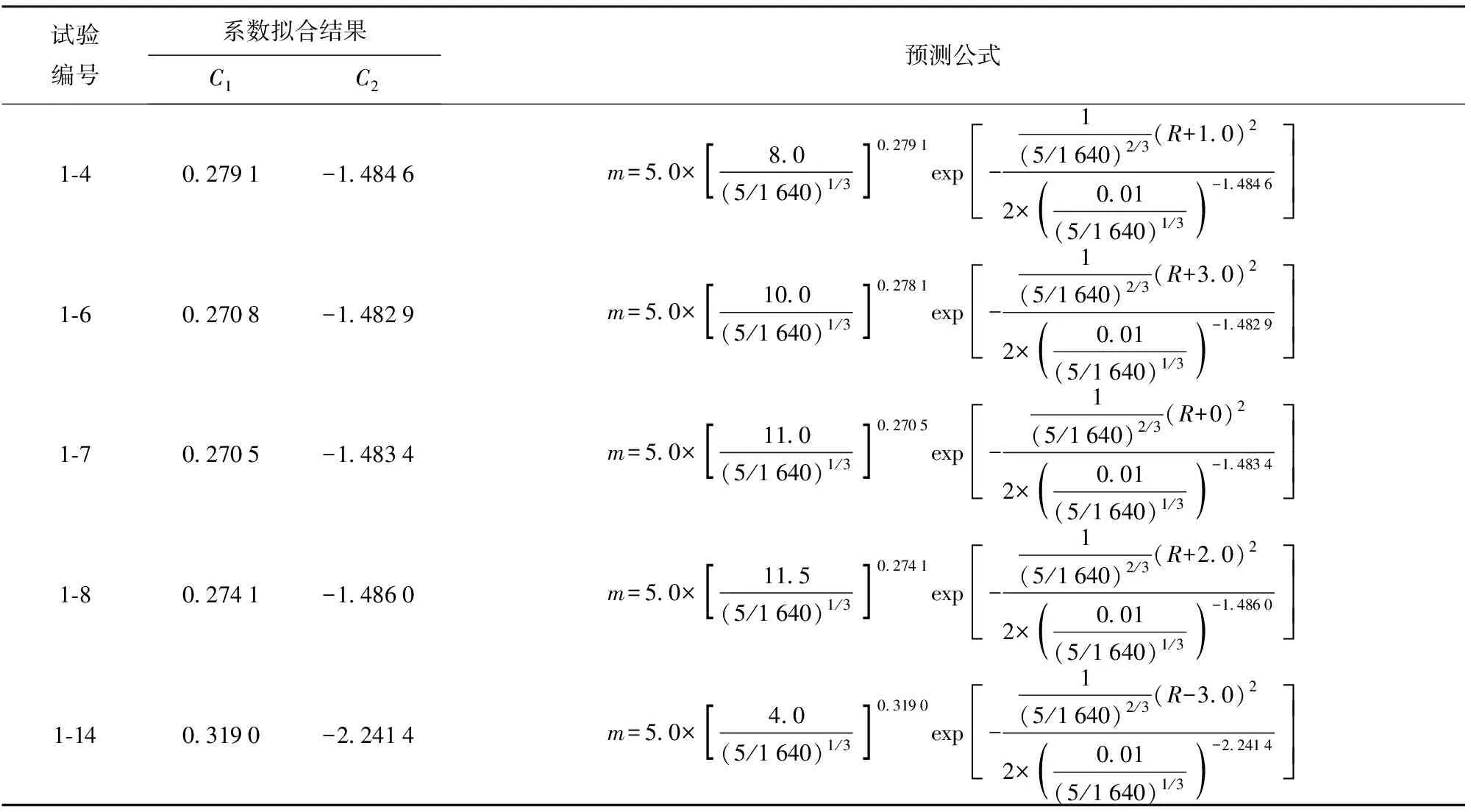
表7 10 mm厚钢化玻璃碎片质量分布预测公式系数拟合结果和预测公式表达式

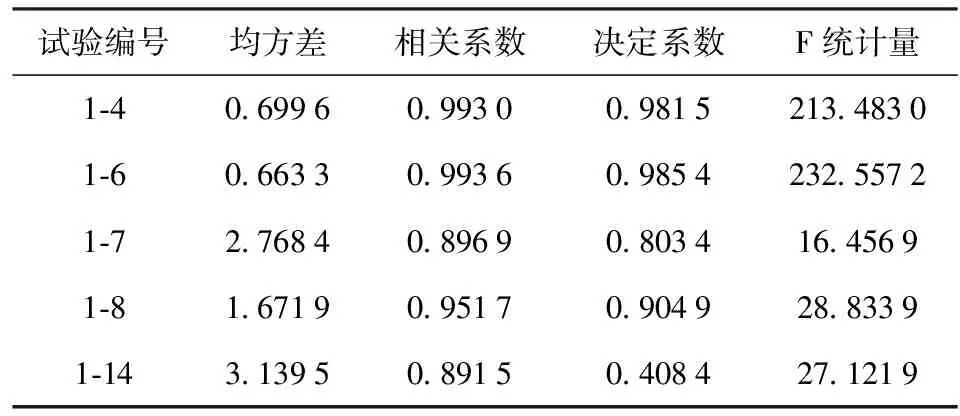
表8 10 mm厚钢化玻璃碎片质量分布预测公式回归分析评价参数

图10表明，1-7试验曲线与试验数据的符合情况较前面2发试验要差，表8中给出的1-7试验的决定系数和相关系数均低于0.9，且均方差稍大而F统计量稍小可以证明上述结论。尽管决定系数和相关系数无法达到最理想的大于0.9的情况，但仍远大于工程上可以接受的最小值0.6，因此，本文认为该发试验的公式预测结果与试验数据基本上是吻合的。

从图12可以看出，1-14试验预测曲线的整体包络虽然看上去能将试验数据包住，但曲线的变化趋势与试验数据符合得较差，上述现象与表8中1-14试验对应的相关系数能够达到0.891 5，但决定系数却只有0.408 4(远低于工程上可以接受的0.6)一致。造成上述符合效果较差的原因分析如下：首先，不同于其他4发试验玻璃碎片往炸药安置点方向飞散的情况(见图6)，1-14试验的玻璃碎片是朝相反的方向飞散的(见图7)，因此，其破坏模式与其他4发试验不相同；另外，最重要的，观察图7发现，1-14试验的玻璃碎片在飞散时会先通过用于安装玻璃的水泥房，试验中测得水泥房在碎片飞散方向上的长度恰好是2.5 m左右，显然，玻璃碎片在飞出水泥房时会有一大部分撞击在水泥房上，然后掉落到地面，同时部分玻璃碎片由于撞击而变得更碎，而过碎的玻璃碎片在试验时没有被统计，因此产生了图12中所示的试验数据分布特点，分布区域中点坐标2.5m处玻璃碎片质量最大，而相邻区域内玻璃碎片质量先减小、后增大。显然，本文的预测公式没办法考虑上述因素的影响，因此吻合效果较差。由于这种情况的试验发次过少(只有1发)，且由于试验设计的缺陷导致破坏情况受水泥房的影响较大，在本文后续内容中将不再分析该发试验。

4.2 6 mm厚钢化玻璃碎片质量分布的预测公式与结果分析

对于6 mm厚钢化玻璃，各发次试验对应(7)式中的基本参数如表9所示。同理，将表9中的数据代入(7)式中，利用表4中的试验结果得到碎片质量m和对应的碎片飞散距离R的数据，使用最小二乘法进行数据拟合，得到各发次试验对应(7)式的系数C1和C2，进而确定各发次试验对应(7)式的确切表达式，结果如表10所示，曲线拟合效果评价参数如表11所示。

根据表10中得到的预测公式，作出碎片质量分布与飞散区域中点坐标的函数曲线，其与试验统计结果的对比如图13和图14所示。

图13和图14表明：预测公式给出的函数曲线与试验统计结果在整体形状上比较吻合，在表11中表现为相关系数在0.8左右；但在局部吻合情况不够理想，具体表现为在图中最大碎片质量位置右侧试验统计结果与预测曲线差别较大，因此，表11中给出的决定系数不是很好。尽管如此，表11的结果表明，决定系数基本上可以认为达到了工程上所能接受的最小值0.6，1-13试验结果的决定系数略小于0.6.

表9 6 mm厚钢化玻璃碎片质量分布预测公式中的基本参数

表10 6 mm厚钢化玻璃碎片质量分布预测公式系数拟合结果和预测公式表达式

表11 6 mm厚钢化玻璃碎片质量分布预测公式回归分析评价参数

总体而言，从工程预估的角度来看，本文得到的玻璃碎片质量分布规律预测公式在所开展的试验中可以看作是准确的。

4.3 综合分析

观察表7和表10可知：对于相同厚度的玻璃，相同的破坏模式下得到的系数C1和C2非常接近，不同破坏模式下的系数C1和C2差别较大；对于不同厚度的玻璃，相同的破坏模式下得到的系数C1和C2的差别也较大。

由于破坏模式2的情况只进行了一发试验，且如前所述，用于安装玻璃的水泥房会对统计带来很大的影响，破坏模式2情况下统计的玻璃碎片本身误差偏大，导致曲线拟合的决定系数低于曲线拟合时可以接受的最小决定系数值0.6，故本文仅给出破坏模式1对应的普适性玻璃碎片质量分布规律预测公式。对不同厚度玻璃的系数C1和C2分别求平均值后保留两位小数，提出可供工程应用参考的玻璃碎片质量分布与碎片飞散距离变化规律的半经验预测公式如(8)式和(9)式所示。

10 mm厚钢化玻璃：

(8)

6 mm厚钢化玻璃：

(9)

5 结论

本文基于试验统计数据和量纲分析方法，研究了钢化玻璃受到冲击波作用破坏后玻璃碎片的质量分布规律，得出结论如下：

1)在所给定的试验条件下，钢化玻璃受到冲击波作用破坏后其碎片质量分布可以表示为关于碎片飞散距离的正态分布函数，如本文(7)式所示。

2)对于不同厚度、相同长度和宽度的钢化玻璃，在相同的破坏模式下，其正态分布函数中的常系数C1和C2不同，且玻璃越厚，C1和C2越大。

3)对于尺寸完全相同的钢化玻璃，如果破坏模式不同，其正态分布函数中的常系数也不同。

4)对于尺寸相同的玻璃，即使爆炸冲击波加载条件不同，只要破坏模式相同，其正态分布函数中的常系数C1和C2可以视为一致的。

因此，在工程应用特别是二次毁伤效应研究中，可以将上述碎片质量分布规律作为参考依据，但要注意公式的使用条件。