弹丸与身管耦合振动问题的迭代解法

姚天乐， 马吉胜， 陶凤和， 齐子元

(陆军工程大学石家庄校区 火炮工程系, 河北 石家庄 050003)

0 引言

火炮射击过程中，身管的自重弯曲、布尔登效应、移动弹丸的重力和偏心力、膛内的旋转摩擦力矩等诸多因素均会影响射击精度。其中，身管振动变形以及弹丸自身惯性是弹丸运动状态改变的一个主要因素。弹丸发射过程是一个极其复杂的动力学过程，发射中，身管振动与弹丸运动相互影响、相互耦合，影响弹丸最终离开炮口的状态。到目前为止，在火炮振动研究领域内，这方面的研究大部分都相对不成熟，准确定量的理论分析还不多见，因而精确地建立弹丸膛内运动引起的炮管振动模型及分析方法是必要的。

对于耦合振动问题的研究，在车辆、桥梁等工程领域有不少值得借鉴的成果[1-4]。在火炮研究领域，康新中等[5]将该类分析方法应用于火炮振动，定性研究了弹丸膛内运动引起的火炮身管横向振动问题。周叮等[6]将小参数法运用于火炮振动领域，研究了弹丸膛内运动引起炮管振动问题，并给出了单发及连发射击时炮管横向振动的解。史跃东等[7]在考虑惯性效应的基础上，研究了身管振动特性，给出了解析解，分析了不同运动参数对炮口振动的影响规律。在忽略移动载荷惯性效应的前提下，姜沐等[8]进一步建立了加速弹丸作用下火炮身管横向振动方程，给出了级数形式的解析解和定量计算结果。马吉胜等[9-10]利用基于Kane方程Huston方法建立了较为完善的研究弹丸与炮管耦合问题的动力学模型，但模型过于复杂，不易实现数值计算。姜沐采用 Picard 迭代法对耦合振动方程进行了重新求解[11]，尽管没有很好地体现载荷的移动性，但对解决耦合振动问题提供了很好的参考。

在以往研究的基础上，本文提出采用迭代的方法对弹丸膛内运动引起的身管振动进行求解，由于程式化好，易于实现数值分析，得到的结论可以为火炮总体设计、结构优化提供参考。

1 耦合振动的动力学

1.1 弹丸的轴向运动规律

弹丸在身管中的运动实际上是十分复杂的动力学过程。因此，为了考虑主要的动力耦合因素，必须将弹丸的动力学过程加以简化，对弹丸在身管中的运动过程进行以下6点假设：

1)忽略弹丸的挤进过程；

2)弹丸和炮膛之间不存在间隙；

3)忽略弹丸在膛内运动的碰撞过程；

4)弹丸出炮口瞬间停止计算；

5)身管在弹丸作用下在垂直平面内运动,忽略弹丸扰动引起的身管振动；

6)身管挠度是小量，弹丸各处的惯性力和离心力在垂直方向。

由常规火炮的工作原理可得到其内弹道方程组为

(1)

式中：ψ为火药已燃相对重量；Z为火药已燃相对厚度；χ、λ、μ、e1为火药形状特征量；u1为燃烧速度系数；l为身管长度，即弹丸全行程长；v为弹丸速度；S为炮膛横断面面积；φ为次要功计算系数；m为弹丸质量，p为弹丸的平均压力；f为火药力；θ为热力学系数；lψ为火药燃烧了ψ时的弹丸行程。

对于(1)式，将进行计算机模型的数值求解。给定参数后，利用龙格- 库塔法按射击过程逐段反复循环逐点求解，最后可得到反映弹丸运动规律的s-t曲线，如图1所示，图中s为弹丸在身管中运动的位移,t为身管自身振动的时间。

1.2 移动弹丸与身管耦合振动分析

在考虑弹丸惯性效应以及身管弯曲变化的前提下，将身管简化欧拉均匀等截面空心悬臂梁，将弹丸简化为忽略形状的质量块。如图2所示，建立直角坐标系，以悬臂梁固定端为坐标原点O，弹丸在身管中沿轴线移动，在身管中的行程规律表示为s(t)。由于身管是连续系统，构造函数y(x,t)来表示身管的振动响应，其中，x是身管各点的位置。由于弹丸在垂直方向上与身管振动同步，弹丸在垂直方向上的位移可表示为t的函数y(s(t),t)。图2中，rc为弹丸所在位置身管的曲率半径。

考虑弹丸对身管的激励作用，对身管进行力学分析，可得到身管的动力学微分方程为

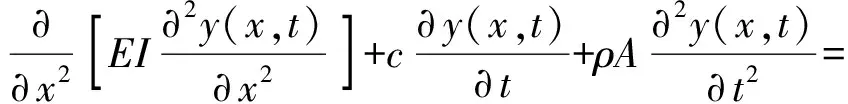
(2)

式中：δ(x-s(t))为Dirac函数，表示弹丸在梁上的位置；fy(x,t)表示弹丸在垂直方向上的受力；E、ρ分别为身管材料的弹性模量和质量密度；c为黏性阻尼系数；A、I分别为截面面积和截面惯性矩。

(2)式的左端描述了身管振动的时空特征，(2)式的右端描述了弹丸的运动状态。在(2)式右端项fy(x,t)的激励作用下，身管进行振动，而身管的振动又会引起弹丸运动状态的改变，从而改变fy(x,t)。同时，身管在振动时，弹丸也在移动，δ(x-s(t))也将随之改变。弹丸在两个方向上的运动状态同时改变，又同时影响身管的振动状态，如果方程右端两项均有清楚的变化规律，则可以得到(2)式的真实解。但是fy(x,t)的确定非常困难，因此(2)式无法进行求解，为此进行如下分析。

设弹丸到身管末端经历的时间序列为

T={t1,t2,…,ti,…,tn},

(3)

由于弹丸的运动位置与运动时间一一对应，则弹丸的移动位置也可离散化，设弹丸运动的位置序列为

s={s1,s2,…,si,…,sn}.

(4)

经过上述处理后，图2所示的弹丸连续移动状态转换为图3所示的对身管离散化激励的状态。由于弹丸移动速度非常大，在弹丸运动期间，身管的阻尼对身管的振动影响较小，因此在计算耦合振动问题时可以忽略阻尼的影响。

按照图3所示，将连续的激励离散化。根据图3，将(2)式转化为n个可处理的非耦合方程如下：

(5)

式中：fy(si,ti)是弹丸在si处时对梁的静态激励。对上述静态方程进行求解，可得到梁静态激励时的响应，可以将此响应作为求解梁在动态激励下实际响应的初值。

1.3 身管横向受力状态动态分析

考虑振动过程中身管各处存在曲率，且身管在弹丸运动过程中持续振动，则弹丸对身管主要存在离心力与惯性力的作用。身管的振动加速度存在向上或向下两种状态，因此，弹丸在垂直方向的受力分析如图4所示，图中fI为弹丸惯性力，F为弹丸向心力，g为重力加速度。

由图4(a)及图4(b)可知，弹丸所受垂直方向上的合力为

fy(x,t)=mg±(fI-F).

(6)

fI与所在处梁的加速度方向相反，大小为

(7)

F指向弹丸所在处梁的曲率中心，大小为

(8)

2 耦合振动模型的迭代解法

取(5)式中的任取方程为例，进行身管响应求解：

(9)

对于(9)式，边界条件与初始条件分别为

(10)

(11)

因为身管的响应，即(9)式的解y(x,t)在时间和空间上是分离的，所以(9)式的解可以写成对应于激励δ(x-si)fy(si,ti)下所有固有振动的叠加。利用振型函数的正交性，将系统物理坐标的偏微分方程变换成一系列固有坐标的常微分方程组，引进广义坐标qr(t)，(9)式的解可写为

(12)

式中：Yr(x)为正则振型函数。

对于身管，由于约束关系已经确定，则与振型函数r阶固有频率ωr相应的振型函数可取为

Yr(x)=cosh(βrx)-cos (βrx)+
ξr[sinh(βrx)-sin(βrx)]，

(13)

式中：

(14)

(15)

对振型函数进行正则化处理，令

(16)

结合(13)式及(16)式，则此时刻的正则振型函数为

Yr(x)=αr{cosh(βrsi)-cos (βrsi)+
ξr[sinh(βrsi)-sin(βrsi)]}.

(17)

(18)

式中：Qr(t)为广义力。对于等截面均质悬臂梁，固有频率为

(19)

对常微分方程(18)式，采用杜哈梅积分进行求解，可得

(20)

(21)

由虚功原理可以分析出对应于广义坐标qr(t)在梁si处由fy(si,ti)计算出的广义力大小为

Qr(t)=fy(si,ti)Yr(si),

(22)

则广义力可表示为

(23)

在耦合振动过程中，弹丸的向心力反作用于身管，改变身管在弹丸所在处的振动加速度。由于弹丸振动加速度与身管振动加速度一致，在迭代过程中，离心力的影响因素已经包含在了弹丸的惯性力中。迭代过程使用的弹丸对身管的激励大小为

fy(x,t)=mg-fI，

(24)

fI的方向由(7)式中计算结果的符号确定。

考虑弹丸的惯性效应后，由(24)式可知，弹丸对身管的激励大小为

(25)

由于弹丸的垂直方向加速度初始值未知，对身管响应进行迭代法求解时，对身管的初次激励设定为弹丸重力：

(26)

联立(17)式、(22)式与(23)式，可得广义力大小为

Qr(t)=mg{αr[cosh(βrsi)-cos(βrsi)+
ξr(sinh(βrsi)-sin(βrsi))]}.

(27)

联立(12)式、(16)式与(21)式可求得弹丸在身管si处初次激励时身管的响应为

(28)

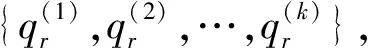
身管在弹丸激励下产生的响应反作用于弹丸，对弹丸进行激励，使弹丸产生响应。此时，弹丸的横向惯性力为

(29)

因此在身管的作用下，弹丸对身管的第2次激励为

(30)

(31)

(32)

(33)

(34)

当弹丸对身管的激励趋于稳定时，可由收敛准则确定最小迭代次数。身管激励的收敛准则为

(35)

3 数值求解结果与分析

应用第2节中的迭代解法对弹丸与身管耦合振动模型进行数值求解。

在数值求解过程中使用的各个基本参数如表1所示。

3.1 身管模态阶数的确定

表1 基本参数

由图6可知，当r>3时，R趋近于0. 设图6所示曲线关系为R=f(r)，在区间[1,3]与[1,∞]上分别对图示曲线进行积分，可得

(36)

由(36)式可知，身管振动主要集中于前3阶模态，取身管振动的前3阶模态可以满足计算精度要求。

3.2 弹丸与身管耦合模型数值求解流程

在确定身管振动的模态结束后，编写程序对身管响应进行迭代法数值求解，采用迭代法编写程序的流程如图7所示。

3.3 身管振动规律分析

采用迭代法求解出弹丸在各点对身管的实际激励，对实际激励在各点的变化规律进行分析。求解出各个时刻身管振动的全貌，取身管振动前期、中期、后期和末期4个时期的振动全貌进行分析。并给出某两个时期的激励收敛过程进行比较，说明激励收敛的规律。

弹丸在运动过程中的惯性力变化如图8所示，对身管的实际激励变化如图9所示。

由图8可知，弹丸在运动的初始阶段，垂直方向的惯性加速度较小，对弹丸运动状态造成的影响也比较小，因此在图9中反映出弹丸对身管的实际激励与弹丸重力十分接近。弹丸在身管中经过加速运动以后，垂直方向加速度产生了变化，由图9可知，弹丸对身管的真实激励在弹丸重力附近波动。数值结果显示，弹丸在出炮口位置惯性力较小，弹丸对身管的激励与弹丸重力大小基本相同。

取弹丸在身管中运动前期、中期、后期和末期身管振动的时空分布图如图10～图13所示。

图10～图13为弹丸的动态过程离散化以后，对某点进行与动态过程等效的实际激励时，在该激励下身管持续振动的全貌图。对应确定的时刻可以得到该时刻身管的振动样貌，对应确定的位置，可以得出某点的振动规律。按照4个时期的顺序观察4幅图可知，随着弹丸在身管中运动，身管整体振动的最大幅值一直从身管始端向身管末端移动。

按照弹丸的行程求解身管炮口处位移，可以得到弹丸运动过程中炮口处位移规律，如图14所示。

在本领域中，国内相关学者在考虑不同因素的影响下，也建立了各种模型求解弹炮耦合问题。刘宁等[12]在考虑横向碰撞的因素下建立了耦合振动模型。郭保全等[13]基于Adams中的柔性体接触理论，建立了弹带和弹丸前定心部与身管内膛的接触模型，得到了该问题的仿真结果。图14所示的数值求解结果与上述文献中炮口位移的数值求解结果具有良好的一致性，从而可以从侧面验证本文方法的正确性。

3.4 激励迭代规律分析

取弹丸在运动前期、中期、后期和末期的迭代过程进行观察，弹丸在4个时期激励迭代过程如图15所示。

由图15可知，在运用迭代法进行身管响应的仿真求解过程中发现，激励是单边收敛的，且迭代过程中激励呈上升趋势，激励在各个时期的收敛过程具有相似性。

取激励在各点的迭代次数如图16所示。

由图16可知，激励在身管各点的迭代次数在弹丸的整个运动过程上呈波动趋势。对比图16和图9可以发现，两幅图之间有相似之处。在弹丸惯性力大的地方相应的激励迭代次数多，惯性力小的地方相应的激励迭代次数少。随着弹丸在身管中运动，弹丸的运动状态变得复杂，弹丸对身管的激励迭代次数始终大于弹丸运动初始时期在各点的迭代次数。

对于火炮的射击问题，普遍关心的是弹丸离开炮口时炮口的振动大小。按照图9所示的规律，激励的波峰随着位移的增大有减小的趋势。因此，可以考虑改善火炮身管和弹丸的结构，优化相关的设计参数，使得耦合振动的波峰提前到来。这是减小火炮射击时炮口振动的一种方法。

4 结论

本文基于迭代法的思想，提出了弹丸与身管耦合振动问题的迭代求解方法，实现了耦合振动的连续过程离散化，构建了迭代解法的程式化流程，使得该方法更加易于实现数值计算。本文的贡献及所得结论如下：

1)通过将弹丸在身管内的运动时间进行离散化处理，实现了耦合振动的连续过程离散化。

2)在主要考虑弹丸的惯性效应和梁的曲率变化这两个因素的综合作用下，采用逐点迭代计算的方法，结合微分方程理论，在给定适当初值的情况下，构造迭代序列对耦合振动系统在各个时刻的实际响应进行逼近，对振动模型进行了数值求解。

3)对各个时刻激励的迭代过程进行分析，发现了在弹丸运行过程中的实际激励在整个过程中的波动变化。

4) 本文数值求解结果与文献[12-13]具有良好的一致性，验证了本文方法的有效性。