车辆电控空气悬挂结构优化模型与优化设计方法研究

雷强顺， 彭友余， 汪国胜， 王超， 宋慧新

(中国北方车辆研究所 底盘技术部, 北京 100072)

0 引言

相关研究与试验表明：安装电控空气悬挂系统(ECASS)的轮式车辆或履带车辆,其越野速度可提高2～3倍,明显加快部队的作战节奏，显著提高平台稳定性、越野行驶时的操控性能,从而使武器发射地点更为灵活,并显著提高武器系统的射击精度；安装ECASS能够显著吸收冲击和震动能量,大幅度减小车辆的相对运动和振动，从而显著提高可靠性,提高乘员工作效率以及车辆装载能力和燃油经济性等[1-4]。鉴于ECASS的优越性能，国内学者开展了相关研究[5-6]。但前期研究表明，按照原有的电控空气悬挂结构参数进行分析，悬挂刚度曲线并不理想(见图1)，导致车辆姿态不一、调节困难并易产生悬挂击穿与脱带现象[5-6]，难以满足相关车辆的行动系统设计要求，因此必须对悬挂结构参数进行优化。

显然，优化设计的前提是有一个明确的优化目标模型与相应的评价方法或评价模型。国内外对于车辆悬挂系统的优化研究主要集中在两个方面：一是以提高车辆行驶平顺性为目的的悬挂刚度与阻尼系数优化[7-9]；二是以提高轮式车辆操稳性为目的的悬挂结构参数优化[7,10-11]。对于车辆平顺性评价方法，国内外学者进行了大量研究，提出了很多平顺性评价方法与评价标准[11-16]，最典型的是国际ISO标准[14-15]、美国陆军试验规程[16]、我国国家军用标准《装甲车辆野外振动试验规程》[17]等。但是这些评价方法主要是针对轮式车辆，且均是在试验数据的基础上进行的。到目前为止，在设计阶段还没有一个公认、统一、系统、与履带车辆行驶平顺性相关的悬挂设计标准或规则，国内外相关的评价指标体系与评价方法仍处于空白。

本文针对文献[5-6]中所述的电控空气悬挂结构设计过程中遇到的问题，在分析电控空气悬挂特性指标、影响因素、约束条件基础上建立了电控空气悬挂结构及参数优化的目标模型，并对其结构及参数进行了优化设计研究，提出了系统的电控空气悬挂结构优化规则与悬挂特性评价方法。

1 电控空气悬挂结构及优化参数范围

电控空气悬挂机构简图如图2所示，空气弹簧结构简图如图3所示。图2和图3中以及电控空气悬挂相关尺寸几何意义见表1和表2，其中活塞杆中空内腔直径dpr,i、长度h、活塞杆外径dpr,o、空气弹簧内径das,i、空气弹簧外径das,o等需要优化的电控空气悬挂相关参数含义及尺寸范围见图3和表2.

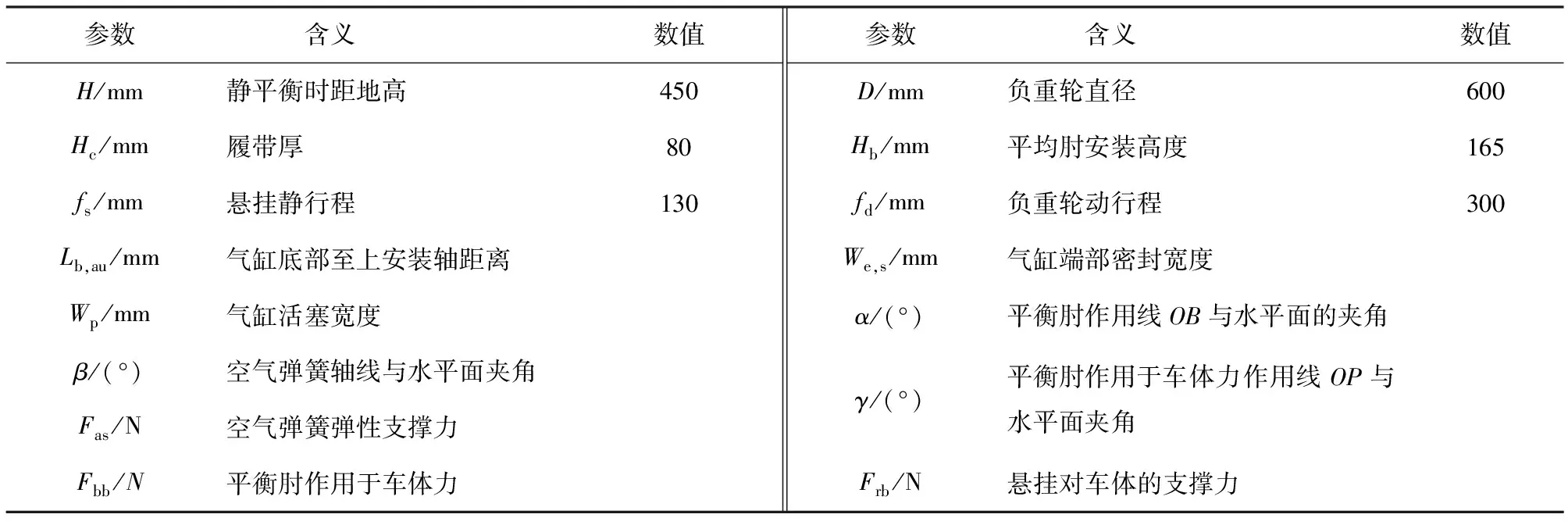
表1 电控空气悬挂结构参数表

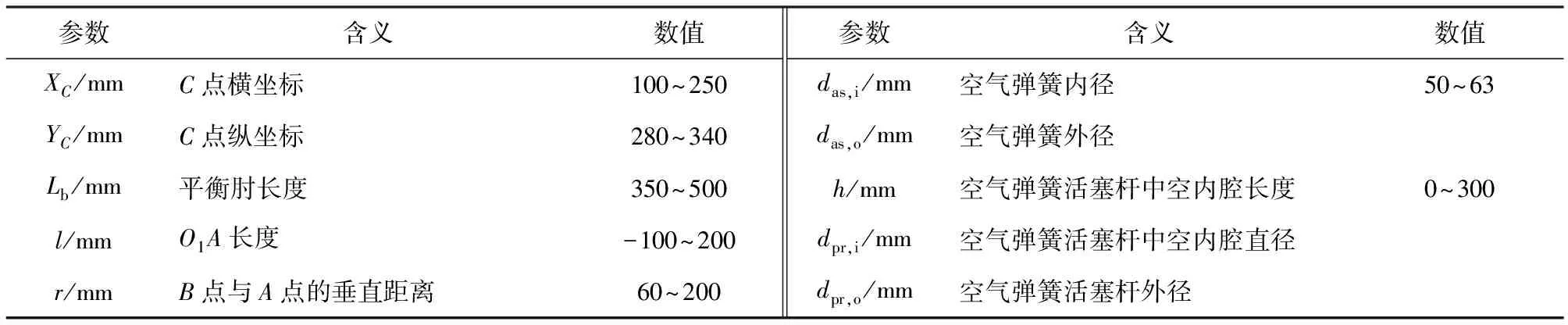
表2 电控空气悬挂结构优化参数及尺寸范围表

2 电控空气悬挂特性及评价指标

单个悬挂特性要求是在保证满足总体结构参数与设计要求情况下，使悬挂刚度曲线形状合理，悬挂的缓冲能力、减振设计与平衡肘受力效果均达到近似理想状态。悬挂特性可以用以下4个评价指标来表达。

2.1 总缓冲势量及总比位能

总缓冲势量E可由(1)式表达：

(1)

式中：pi为空气弹簧初始充气压力；Vi为空气弹簧初始充气时的气体体积；V为任意位置时空气弹簧内的压缩气体体积；Av为空气弹簧活塞杆有效面积；s、ss和sd分别为空气弹簧活塞行程、静行程、动行程；τ为压缩气体的多变指数，τ=1.25.

总比位能[17]概念是针对整车的缓冲能力提出的，一般认为，其值越大，悬挂缓冲能力越强，悬挂发生悬挂击穿的概率越小。对于装备空气弹簧的单个悬挂系统，总比位能λt为动比位能λd与静比位能λs之和，λd、λs可分别通过(2)式、(3)式计算如下：

(2)

(3)

式中:Gk为第k个悬挂簧上质量；Fas,k为第k个悬挂空气弹簧弹性支撑力。

2.2 垂直振动周期

文献[18]与实车试验实践均表明，坦克装甲车辆振动频率越低，振幅越小，振动加速度和速度越小，则坦克装甲车辆行驶的平稳性就越好。为此要求悬挂平均刚度要适当小一些(即悬挂稍软一些)，z向垂直线振动周期Tz和绕横轴y的纵向角振动周期Ty要适当大一些。垂直振动周期可由(4)式估计：

(4)

式中：m为整车簧上质量；Kk为第k个悬挂的垂直刚度；n为轮对数。

在行动总体参数没有确定情况下，对于单个悬挂的设计，垂直振动周期可采用(5)式估计：

(5)

式中：mk为需要优化计算的第k个悬挂所承担的负载质量。

由负重轮作用于平衡肘的支撑力Frb、空气弹簧弹性支撑力Fas、平衡肘与车体之间的作用力Fbb关系，可推导电控空气悬挂单个悬挂装置的刚度K[6]为

(6)

式中：pi和Vi分别为初始安装状态下空气弹簧内的压力与容积；ps和Vs分别为静平衡状态下空气弹簧内的压力与容积；f为悬挂行程；

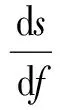
(7)

(8)

(9)

(10)

2.3 纵向角振动周期

纵向角振动周期Ty可由(11)式估计：

(11)

对于特定装甲车辆，在车体质量与尺寸确定情况下，轮系布置变化不大，因此纵向角振动周期Ty变化不大，可优化的空间较小，在单个悬挂设计阶段可不予考虑。

2.4 空气弹簧作用于平衡肘的传动角

除悬挂缓冲性能外，平衡肘受力效果对平衡肘自身及轴承寿命有较大影响。空气弹簧作用于平衡肘的传动角δ[6]越大，平衡肘受力效果越好。为考察空气弹簧弹性支撑力作用效果与平衡肘的受力效果，需要考察空气弹簧弹性支撑力Fas作用于平衡肘的传动角。

由图2所示几何关系可知Fas作用于平衡肘的传动角为

δ=β-ε，

(12)

式中：ε为OB力作用线与水平面的夹角，

ε=αtan(YB/XB),

(13)

XB和YB为B点坐标。

由于平衡肘工作在静平衡状态的工作概率最高，且在动行程末端其受力最恶劣，在这两种状态下静传动角δs与动传动角δd均要考虑。

3 单个悬挂特性的结构影响因素

3.1 平衡肘长度

平衡肘长度Lb影响到悬挂的动行程、静行程、悬挂空气弹簧的内部压强及悬挂刚度特性。增加平衡肘长度有利于避免悬挂零件之间的干涉，并改变空气弹簧的工作传动角δ.

如图4所示，当XC=210 mm，YC=330 mm，das,i=56 mm，l=85 mm，r=50 mm，h=0 mm,Lb=400 mm时，在动行程的末端f=430 mm附近出现压缩空气体积V<0的情况，表明活塞已抵达缸筒底部且发生了严重干涉。

如图5和图6所示，当XC=210 mm，YC=330 mm，das,i=56 mm，l=85 mm，r=50 mm，h=0 mm，Lb=420 mm时，在动行程的末端虽然没有发生干涉，但是由于悬挂在较短动行程内的空气弹簧压缩量较大，导致悬挂支撑力(实际为负重轮作用于平衡肘的力Frb)悬挂等效刚度Ke发生较大变化。显然，这些情况对悬挂工作是不允许的。

从图4～图6可以看出，平衡肘长度对悬挂干涉及刚度特性影响确实较大。

3.2 弹簧上、下支点位置参数

如图2所示，增加XC、YC或减小l、r，可减小空气弹簧倾斜角度，有利于改善悬挂的受力效果。由于上支点距平衡肘在车体上的安装点竖直距离YC受整个履带环高度限制，不能增加太多。

3.3 空气弹簧内径与活塞杆中空内腔直径及深度

当空气弹簧内径das,i=56 mm、其他参数在表2中的范围内进行优化时，都会在动行程末端出现压力超过密封压力限值(40 MPa)的情况(见图7)。因此，为避免弹簧在悬挂动行程末端内部压力太大，根本的解决方法就是增大弹簧体积(内径或深度)。由于增大直径受车体侧向布置空间限制，空气弹簧内径das,i不宜增加太多。为此，ECASS采取了中空活塞杆增加压缩空气体积的方案，其相应的参数有活塞杆中空内腔直径dpr,i及长度h.

4 约束条件

在优化过程中发现：如果改变上支点位置，则会使弹簧行程减小，并会导致内部干涉；其次，平衡肘受力效果、悬挂特性也不会达到最优。因此，在对整个悬挂结构综合优化之前，有必要分析约束条件。

4.1 弹簧与平衡肘大头不干涉约束

如图8所示，在下限位或初始安装位置，空气弹簧缸筒外表面与电磁致动器相切，过电磁致动器中心作空气弹簧中心线的垂线，其垂足为Q，则OC与垂直线的夹角为

θ=αtan(XC/YC),

(14)

CQ与垂直线的夹角为

(15)

式中：da,o为电磁致动器外径。则弹簧与平衡肘大头不干涉约束为

ψ-θ>0°.

(16)

4.2 弹簧动、静行程约束

如图3所示的空气弹簧内部结构，在悬挂处于最大动行程(对应上限位)状态下，活塞端面几乎抵至气缸底部，设上安装轴与气缸底部距离为Lb,ua，气缸口密封宽度为We,s，上安装轴与气缸口距离为Lua,e，活塞杆有效长度为Lpr，气缸活塞宽度为Wp，此时空气弹簧长度(上、下安装轴距离)为Las. 为避免活塞与气缸底部发生硬性碰撞(活塞端面至气缸底部距离不小于Δs=10 mm)，其对应的动行程约束条件为

Las,u+Lb,ua-Lpr≥Δs,

(17)

式中：Las,u为空气弹簧在上限位置时上、下安装轴之间的距离。

当空气弹簧处于自由充气状态下，平衡肘处于下限位，此时活塞相对气缸的位置如图8所示。为使活塞保持一定的导向长度，活塞右端面与气缸口的距离必须大于活塞长度，此时静行程约束为

(Lpr-Wp)-(Las,d-Lua,e+We,s)≥Δs,

(18)

式中：Las,d为空气弹簧在下限位置时上、下安装轴之间的距离。

4.3 弹簧内部压力约束

当平衡肘处于上限位状态下弹簧内部压力才达到最大时，由于国内液压动密封当前能达到40 MPa，弹簧内部压力约束为

pd≤[pd]=40 MPa.

(19)

4.4 悬挂刚度

文献[6]中的研究表明，如果结构设计得不好，则会出现图1中刚度特性曲线所示的下凹现象，导致姿态不一，为此必须对刚度曲线形状加以限制。避免这种现象出现的约束条件为

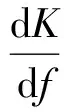
(20)

对于如图1所示的摆动缸式空气弹簧悬挂刚度特性曲线，其只能有一个上凹处。此时，(20)式所示的条件可简化为

minK>0.

(21)

综合上述各约束条件，可得总约束条件为

(22)

5 悬挂结构综合优化

5.1 电控空气悬挂结构优化目标模型

根据前文分析的悬挂特性评价指标与约束条件，可建立电控空气悬挂结构优化目标函数为

(23)

式中：ks、kd、kz和kδ分别为与各项评价指标对应的评价权数；[λs]、[λd]和[Tz]分别表示相应指标对应的阈值。根据表1所示的行动总体设计参数，可取[λs]=fs=130 mm，[λd]=fd=300 mm；根据文献[17]，其垂直振动周期与角振动周期分别要求不低于1.0 s与1.6 s，可取[Tz]=1.0 s，[Ty]=1.6 s，对于单个悬挂的评价，可忽略Ty对应的评价项。

因此，(23)式与(22)式一起构成了电控空气悬挂结构优化的目标数学模型。

采用反复试凑法进行验算，发现当ks=0.5，kd=3，kz=1，kδ=1时，其对应的悬挂特性曲线基本达到上述要求。

5.2 电控空气悬挂结构优化分析

按照上述目标模型、优化方法与图9所示的步骤进行结构优化，优化结果见表3及图10～图15.

表3 优化后电控空气悬挂结构参数表

从表3及图10～图15中可见，经过结构优化后的电控空气悬挂避免了结构干涉，且总比位能λt=607.1 mm与动比位能λd=489.2 mm均超过设计要求，悬挂具有较强的缓冲能力，在承担对应的静态质量载荷下，其静态振动周期Tz=1.1 s，刚度特性曲线非常理想。无论缓冲可靠性还是减振性能均较好，满足了前期悬挂设计与后期实车行驶的多方面要求。

6 结论

1)优化后的结构参数能满足多重约束与多目标的行动系统设计要求，并使悬挂缓冲性能与平衡肘受力效果达到比较理想状态。

2)电控空气悬挂结构优化目标模型合理、科学，体现了前期悬挂设计与后期实车行驶的多方面要求，解决了工程设计中的结构设计问题。

3)基于多重约束、最大缓冲势能、振动周期与平衡肘传动效果加权值最大化的多目标结构优化设计方法是有效、科学的，能指导基于ECASS悬挂的结构设计与摆动缸式油气悬挂的设计。

4)由于电控空气悬挂结构与一般履带车辆悬挂结构类似，本文所述的悬挂结构优化目标模型适用带平衡肘的履带式装甲车辆悬挂结构优化，具有较强的通用性。