混合式惯性导航系统全数字平台技术研究
王蕾, 王玮, 刘增军, 宋天骁
(北京航空航天大学 仪器科学与光电工程学院, 北京 100191)
0 引言
混合式惯性导航(简称惯导)系统吸收了平台式、捷联式和旋转式惯导系统的各自优点,不仅能大幅度提高导航定位精度、实现快速精确自对准,还可实现装机条件下的自标定以及明显降低购置与维护成本,能满足高速和高动态等运载器对高精度惯导系统提出的新需求[1-2]。将基于数字伺服控制的物理稳定平台与基于捷联姿态计算的数学平台有机结合是混合式惯导系统的首要特征。但是在物理稳定平台方面,混合式惯导系统相较于平台式惯导系统已有很大改变。
在可靠性方面,混合式惯导系统的物理平台有了极大的提高。首先,它采用全数字控制方式,陀螺信号数字输出直接进入计算机,由陀螺信号生成控制信号的过程全部在计算机内完成,从而省去了以往平台式惯导系统中的前置放大器、解调器、方位坐标分解器和正割分解器等诸多部件。另外,以往平台式惯导系统中使用的轴角传感器主要是旋转变压器,其输出信号还需要经过R/D转换等才能进入计算机[3];混合式惯导系统的轴角传感器采用光栅传感器,其数字输出信号可直接进入计算机,因此平台所需部件的种类和数量都大大减少,潜在产生问题的根源也相应减少,系统的可靠性提升。
其次,以往的平台式惯导系统将陀螺和加速度计的信号传送给平台外的导航计算机,每一路陀螺和加速度计信号都会占用至少一环导电滑环,再加上其他一些信号,导电滑环的环数能达到六七十,大大增加了滑环的长度,也增大了平台的体积;混合式惯导系统将陀螺和加速度计的信息汇总后通过总线形式传输,所需导电滑环的环数大大减少。
另外,平台式惯导系统始终稳定于导航坐标系[4],其导电滑环的电刷基本在同一个位置附近摩擦,滑环寿命衰减较快;混合式惯导系统通过旋转调制,使平台作周期性地旋转运动[5],滑环的电刷与每一个位置接触,而不再是摩擦同一个位置,因此延长了滑环的使用寿命。
在平台的功能和工作模式方面,混合式惯导系统不仅要像平台式惯导系统一样实现稳定功能,隔离载体的角运动,而且还需要同时实现旋转的功能,从而使惯性器件的旋转相对于导航坐标系进行,实现更优的误差调制效果[6]。因此,混合式惯导系统的物理平台包括了稳定、锁定、稳定加旋转等多种工作模式,特别是稳定加旋转的工作模式是因混合式惯性导航系统技术途径而产生的新需求,也是它与平台式惯导和旋转式惯导在平台控制上的最大区别。本文主要从平台结构和稳定加旋转的控制算法两方面出发,针对混合式惯导系统在不同工作阶段的控制需求展开分析和研究。
1 全数字物理平台设计
1.1 平台结构组成
混合式惯导系统的物理平台采用全数字控制以后,平台结构得到极大简化,框架上只剩下电机、导电滑环和光栅。电机采用直流无刷电机,可避免有刷电机电刷易磨损、打火等问题,导电滑环采用封闭式滑环,这些对于提高系统的可靠性都极为有利。混合式惯导系统的惯性测量单元(IMU)数据采用总线的形式打包输出,因此平台上的线缆数量大大减少,通常十几环的滑环就足够。对于一些不存在大角运动的应用领域,也可以用软导线代替导电滑环。混合式惯导系统在集合平台式、捷联式和旋转式各类惯导系统优点后,可以由惯性器件的数据直接计算出高精度的速度和位置信息。但是,若要输出与速度、位置相匹配的高精度载体姿态/航向信息,还需要有高精度的平台框架转角值,因此框架的轴角传感器采用圆光栅传感器,其分辨率和精度都远远高于以往平台使用的旋转变压器和码盘。特别是经过近些年的技术发展,目前市面上的光栅在抵抗冲击震动和耐低温的能力上已经有了显著提高。另外,圆光栅通常为扁平结构,其内径较大,可以与轴承等部件做嵌套设计,这对于减小系统体积有极大贡献。当然,在安装和使用过程中需要解决偏心等问题,才能保证较高的使用精度[7]。
根据应用场合的不同,混合式惯导系统的物理平台在结构上可以是三框架形式,也可以是双框架形式,还可以是单框架形式。三框架形式的平台能隔离载体各个方向的角运动,在运载器姿态运动比较灵活的应用场合更有优势。而且由于系统采用了捷联的算法,混合式惯导仅用三框架平台就能解决以往需要四框架平台才能解决的奇异区控制问题。图1是一个三框架结构平台示意图,内框架轴为方位轴Z,中框架轴为俯仰轴X,外框架轴为横滚轴Y. 每个框架上各安装一个直流无刷电机和光栅,内框安装光栅的一端再安装一个导电滑环,另外两个框使用软导线。而对于载体姿态运动比较单一的场合,混合式惯导系统也可采用双框架或单框架结构形式,这时在姿态运动较小的方向平台不做隔离。而不被隔离的这一部分角运动和平台的控制误差角同样都可以通过系统的捷联计算来解决。
采用数字式平台以后,平台的控制电路也相应得到简化。控制电路主要包括控制计算机和功率放大器,功率放大器再采用集成电路,因此控制电路所占体积很小,可以整体放置在平台外。由于混合式惯导系统的平台控制还需要用到导航计算的结果,使各环架之间的控制相互关联,若将每个环架的控制电路分别置于相应的环架上,反而会给系统设计带来不便。
1.2 平台工作模式
当混合式惯导系统分别处于自标定、自对准和导航阶段时,其物理平台的工作模式也有所区别。例如在自标定阶段,物理平台主要工作于锁定状态,IMU被锁定在不同的位置以激励出惯性器件的各项误差[8]。而在自对准阶段,混合式惯导系统工作在稳定加旋转的模式,一方面可降低载体晃动给对准精度带来的影响,一方面可采用旋转对准法来提高对准精度,并缩短对准时间[9]。在导航阶段,根据应用场合的不同,物理平台可以工作在锁定、稳定、稳定加旋转3种模式。
具体而言,对于锁定模式,混合式惯导系统物理平台以框架上的光栅作为控制回路的反馈元件,实现闭环电锁定。目前在一些航天领域使用的“三自”(自主功能检测、自主误差标定、自主初始对准)惯性测量组件也有与混合式惯导系统类似的旋转机构[10],同样也有锁定的工作模式。但是当进入导航状态以后,“三自”惯性测量组件的锁定采用的是机械锁定。这种锁定方式需要在旋转轴上再安装端齿盘等机械锁定装置,使得系统的体积和质量明显增加。混合式惯导系统采用电锁定的方式,只要电机的力矩足够大,即使载体出现了大过载,也不会产生失锁的现象。平台式惯导系统也没有使用机械锁定,在大过载时也是通过平台自身的电机来抵抗外力矩,因此混合式惯导系统采用电锁定这种方式是可靠的。当然,这种电锁定的方式对系统的结构设计和加工提出了很高的要求。设计和加工装配过程中都需要严格控制旋转体的质心与几何中心之间的重合度,否则在大过载情况下由于这种偏心所带来的不平衡力矩会大大影响锁定的效果。
对于稳定模式,混合式惯导系统以陀螺作为平台稳定控制回路的反馈元件,这与传统平台式惯导系统的稳定回路类似。平台式惯导通常以挠性陀螺、三浮陀螺等机械式陀螺来建立模拟式稳定回路,这类稳定回路的结构相对复杂,可靠性也不高。随着科技的发展,计算机的计算能力提高,混合式惯导系统采用全数字式稳定回路,陀螺的原始输出信号直接进入到计算机,在计算机内完成信号的处理,最后计算机再输出调宽信号,经功率放大之后去驱动电机,从而减少部件,大大简化系统结构,提升系统可靠性和寿命[11]。混合式惯导系统目前主要采用光纤或激光陀螺,其输出量为角速度信息,为克服角度控制静差,这种情况不宜直接使用传统PID控制,需增加一级积分,采用PII2控制[12]。
稳定加旋转的模式是混合式惯导系统新增加的一种平台工作状态,这要求物理平台在稳定的基础上再使IMU平稳旋转,以达到更好的旋转调制效果。传统平台式惯导系统只有稳定无旋转,旋转式惯导只有旋转无稳定[13],混合式惯导要实现稳定加旋转的平台工作模式,它们之间是否会产生相互干扰,这里的旋转是否还能平稳,需要研究。下文将针对平台的这一新工作模式进行控制算法研究。
2 稳定加旋转模式的控制指令算法
2.1 控制回路模型

当平台只有一个旋转轴时,总有一个陀螺的敏感轴方向与平台的这一旋转轴方向保持一致,因此平台的控制指令角速度可直接由该陀螺的数据计算得到。当平台有多个旋转轴时,在稳定加旋转这种工作模式中,陀螺敏感轴的指向不再固定,不能再直接根据陀螺的测量值来控制平台,需要经过一定的转换。因此此时图2中ωC的值需要根据3个陀螺的数据综合得到,通过计算出惯性测量单元的运动角速度在各电机轴方向的分量后进行PII2控制。
2.2 指令角速度计算

(1)

(2)
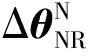
(3)
式中:ψ为载体的方位角。
(4)
最后,将游移方位坐标系下的指令角速度再分解到3个电机轴的方向,如(5)式所示:
(5)
3 实验验证
3.1 实验方法
光纤陀螺三轴混合式惯导系统(见图4)先静止放置,待系统启动并进入稳定加旋转工作模式后开始实验。在绕内框方位轴的第1个正反转时,系统仍保持静止,不加扰动,验证该控制方法在平稳旋转过程中的控制性能。在第2个正反转时,正转和反转都沿方位轴方向手动给惯导系统施加角速度扰动。采集该过程中平台框架轴上的光栅输出以及由捷联姿态计算给出的惯性测量单元姿态/航向角。惯性测量单元的俯仰和横滚姿态角直接反映平台在这两个方向的控制误差(若无控制误差,这两个姿态角应始终被控制为0),而航向角要在扣除旋转分量之后才反映平台在该方向的控制误差。另外,内框光栅输出的角度扣除旋转分量后反映载体航向角,经过微分后,反映载体航向运动角速度,即扰动角速度的大小。
3.2 静态实验结果
图5为某次载体保持静止时的实验测试结果。由图5可见:当惯性测量单元绕内框方位轴稳定加旋转且载体静止时,无论是正向旋转还是反向旋转,水平两个方向此时的功能主要是稳定,其控制误差只有约1″;方位轴既稳定又旋转,虽然实现的功能更多,但其控制误差也只有约2″,此时影响控制误差的因素主要为陀螺的分辨率。该光纤陀螺以脉冲形式输出角增量,一个脉冲代表的角增量约0.56″,此时的控制误差实际上只对应于几个陀螺脉冲,因此已经取得了很好的控制效果。另外,对于混合式惯导系统而言,虽然还存在这几个角秒的控制误差,但是它可被系统实时计算得到,并在导航计算时进行软件补偿,因此它已经不会对系统的导航精度造成影响。
3.3 动态实验结果
图6为载体有航向运动时的稳定加旋转控制误差测试实验结果。当载体有角运动时,控制系统立即进行调节,会产生一定的控制误差。从图6中可以看出,当载体航向运动角速度高达50°/s时,相应的最大控制误差角也不超过30″(水平两个方向只有约10″),达到了较好的控制效果。而且与传统平台式惯导系统不同的是,这部分控制误差还可以通过混合式惯导系统中的捷联计算作进一步数学补偿修正,因此它对系统导航定位精度的影响更小。
另外,对比图6(a)正转和图6(b)反转的台体航向误差角可以发现,4次正负扰动过程中,都只有两次同方向的扰动产生了较大的航向控制误差。这主要是因为:载体的扰动是通过轴间摩擦传递给台体的,摩擦力矩大小在相对运动的方向不变时是基本保持不变的(即使相对运动的速度大小发生了变化),只有当旋转方向改变时摩擦力矩才会产生较大变化,进而电机施加相应的控制力矩进行调节。图7为摩擦力矩示意图。以图6(a)台体正向旋转为例,无干扰时框架相对于台体的运动角速度Δω0<0,摩擦力矩MT0<0,即工作于图7的位置0;在第135 s附近,当载体有正向的最大约70°/s航向角运动时(载体航向角是以绕Z轴负方向旋转为正),框架相对于台体的运动角速度为Δω1=Δω0-70°/s<0,对应摩擦力矩MT1<0,且MT1≈MT0,因此此时摩擦力矩较之前基本无变化,不会产生大的航向控制误差角;相反,在第137 s附近,载体有负向的最大约50°/s航向角运动,框架相对于台体的运动角速度为Δω2=Δω0+50°/s,从图6(a)的第1幅图可以看出,实验中Δω0≈-6°/s,因此Δω2>0,对应摩擦力矩MT2>0,摩擦力矩较扰动前的MT0发生了较大改变,从而产生明显的调节过程。
4 结论
本文对混合式惯导系统中的物理平台进行了全数字化的结构和控制算法设计。实验测试结果表明:
1) 该控制系统在静止环境下的最大稳定加旋转误差角约1″~2″,在实验给定的一种动态环境下最大稳定加旋转误差角优于30″.
2) 全数字式平台设计不仅降低了系统的复杂程度,减小了体积和质量,提高了可靠性,而且可实现混合式惯导系统的各种功能需求,特别是在稳定加旋转的平台全新工作模式下达到了较高的控制精度。

