浅谈中职分段函数的情境应用教学

◎洪丽莉

分段函数在生活中的应用很广泛，笔者在讲到分段函数的内容时，考虑到中职的学生数学基础较薄弱，对纯理论的数学教学较不感兴趣，因此，笔者结合学生的学习情况和性格特征设计了贴近学生生活的分段函数情境例题，以此来提高学生的学习兴趣和学习热情。

对中职学生来讲，分段函数的例题既要符合他们的学习能力，同时也得具备实用性，因此在例题的设计上，笔者主要以生活实例为主，同时兼顾学生的学习能力，从而让学生感受到例题的社会性和趣味性。在分段函数应用题讲解过程中，要注意引导学生数学建模的思想，数学建模就是将实际问题转化为数学问题，用数学表达式或数学语言来描述实际问题，化繁为简，最后根据计算结果来解决实际问题。

一、分段函数在商品促销里的情境应用教学

例1：超市里某品牌巧克力奶糖进行促销，其售价如下表所示：

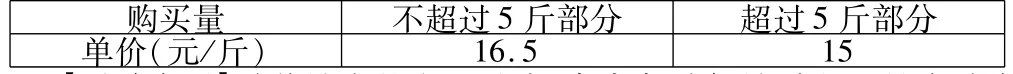
【设计意图】随着社会的发展进步，商家各种促销手段也是多种多样，本道题目的设计以超市买东西为背景，贴合生活情境，题目简单，学生容易做题。

【分析】在数学建模前得先假设购买量为x斤，应付款为y元，在购买斤数不超过5斤时，只要单价×购买量，就可以算出应付款，但是学生在解答时容易将第一个解析式里x的取值范围写成x≤5，之所以会犯这样的错是因为学生忽略了这道题目的背景是买东西，x代表的是购买的斤数，不可能为负数，因此教师在讲解时，一定得特别注意这道题目的定义域。对于第二个解析式，部分学生审题不认真的话很容易直接按照单价×购买量计算，而忽略这里得分为超过和不超过5斤两种情况。同时教师在讲解时要跟学生强调分段函数是一个函数，不是多个函数，只是在不同的取值范围内，有不同的解析式。本道题目重点考查学生分段函数的定义域和审题，由于学生思考问题不够全面，这里就容易犯错了。

通过例1的解答，学生对分段函数的实际应用有了一定的了解，接下来，笔者马上给出了第二道例题。

例2：某品牌服装的天猫旗舰店五一做促销活动，规定如下 ：①如一次性购物不超过500元，不予以折扣；②如一次性购物超过500元但不超过1000元，按标价给予9折优惠；③如一次性购物超过1000元，其中1000元给予9折优惠，超过1000的部分给予8折优惠。（1）试建立购物总标价x元与应付款y元之间的函数关系式。

（2）五一当天，顾客小李两次来这家旗舰店买衣服，分别付款350元和756元，如果小李是一次性购买这些衣服，需要付多少钱呢？

【设计意图】本道题以学生所熟悉的网购为背景，这样的题目设置一方面与现在的网购促销相结合，体现了数学与实际生活的直接联系，另一方面生活化的题目能大大地提高学生的学习兴趣。

解：（1）由题意得

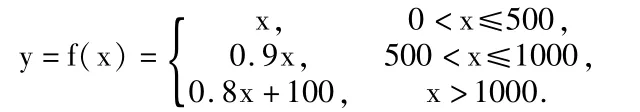
【分析】有了例1为基础，这道题目的定义域学生比较不会写错了，但是在用数学语言列函数式时，还是有一部分同学无法描述清楚，这说明数学建模对学生来讲，还是比较抽象，难以熟练应用，这需要学生多做些题目进行巩固练习。第二小题计算价差的情况，在生活中的实体店或是网店的促销很经常看得到。如果商品的总价越高，则会产生越大的价格差。为了节省资金，可以利用数学模型进行计算和规划，从而可以正确地指导购买决策。

以人类命运共同体为镜像观照新时代统一战线的逻辑前提是发现并归纳二者的强关联性，探讨二者的互动性、互鉴性，探寻有效的合作之道。在思想渊源、奋斗目标、价值取向、主体意识、实践方式等方面，人类命运共同体与新时代统一战线高度契合，具有共通之处。

二、分段函数在企业中的情境应用教学

例3：国务院规定自2011年9月1日起施行新的个税法条例，应税收入不超过3500元，免征个人所得税，超过3500元部分则要征税，个人所得税计算公式：

应缴个人所得税＝（月应税收入－3500）*税率－速算扣除数

已知1－3级个人应纳税额的分段函数为：

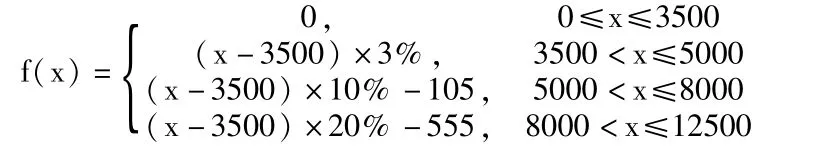
其中x为月应税收入，f（x）为应纳税额，

（1）某财务公司2018年2月新进一名财务人员小王，已知小王的月应税收入是4500元，求小王每月应缴交多少个人所得税？

（2）学校财会专业校友小张，在校期间学习刻苦，认真学习专业知识，2012年毕业后去该财务公司当财务助理，2018年1月，他荣升为财务主管，假如小张现在每月应缴的个人所得税为340元，请问小张的月应税收入为多少元？

【设计意图】本题以学校的校友为背景，结合财会专业，给学生介绍了优秀校友的事迹，让学生对自己的专业有个美好的愿景，以此鼓励学生认真钻研专业知识，为以后的工作打下坚实的基础。同时，本题将分段函数和个人所得税的计算融合在一起，结合个人所得税计算公式，给学生普及了个人所得税的计算方法，让学生很好地体会到了分段函数在个人所得税的应用，让他们能学以致用。

解：（1）由题意得，

f（4500）＝（4500－3500）×3% ＝30

（2）当 x＝5000时，（ ）f 5000 ＝（5000－3500）×3%＝45，

当x＝8000时，（ ）f 8000 ＝（8000－3500）×10%－105＝345，

由此可知，小张月应税收入在5000＜x≤8000内，

由f（x）＝340可得

（x－3500）×10%－105＝340

解得：x＝7950

答：小王每月应缴30元个人所得税；小张的月应税收入为7950元。

【分析】这道题目的第（2）小题是已知函数值，求x的值，这里需要学生选择正确的解析式来代入，而解析式的选择正是本道题目的难点所在，所以教师在讲解时，要注意引导学生找出定义域里的两个分界值5000和8000，将这两个分界值分别代入相应的解析式内，算出相应的个人所得税，从而就可以找出个人所得税为340元时所属的解析式。

例4：小李从中专毕业后，进入了某服装公司工作，该公司有着很规范的管理制度，针对员工的迟到现象采用了分段罚款的措施，迟到时间x分钟与罚款金额y元之间的关系如下所示：

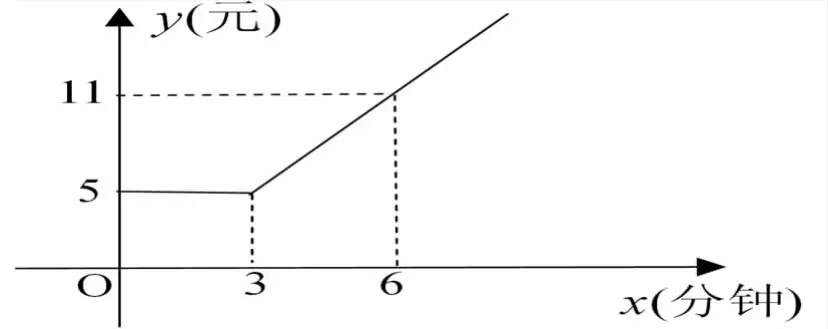
（1）当x≥3时，请写出罚款金额y元与迟到时间x分钟之间的函数关系式

（2）若员工小李迟到2分钟，员工小陈迟到8分钟，分别求出他们的罚款金额。

【设计意图】本题以企业的管理制度为背景，根据迟到的罚款金额和迟到时间来设置分段函数例题，让学生知道了各个不同的企业都有相应的管理制度，这道题目提醒了学生要有时间观念，工作之后得认真遵守企业的管理制度。

解：（1）当x≥3时，设y与x之间的函数关系式为y＝kx＋b，

由图可知：当 x＝3时，y＝5；x＝6时，y＝11，

∴ 当x≥3时，函数关系式为y＝2x－1.

（2）由图可知当 x＝2时，y＝5（元）；

当x＝8时，y＝2×8－1＝15（元）

【分析】本道题目通过图像让学生写出函数的解析式，这里用到了待定系数法来求解的技巧，学生只要能找到图像上的两个点，代入y＝kx＋b，就可以顺利地求解出来，但是在教学过程中发现有部分学生不懂得使用直线方程y＝kx＋b，笔者认为对于一些常用的函数解析式需要教师不断地提醒，才能让学生熟练应用。

本节课所设置的四道情景例题，题目贴合实际生活，学生容易产生共鸣，很好地吸引了学生的注意力，在题目难度的设计上，结合学生的学习基础，由简到难，符合中职学生的认知规律，题目新颖，根据学生以后就业可能会面临到的问题为背景，结合实际情况，设置情景例题，调动了学生的情绪，让学生体验到了数学在生活中存在实用性，从而培养学生利用数学知识来解决实际生活中碰到的数学问题。教师在教学过程中要注意将数学理论知识与生活实际联系在一起，同时跟学生不断强调分段函数的注意事项，让学生在做题过程中能产生成就感，从而激发学生继续学习的信心。