一题多变练思维 多题归一找本质

◎陈红伟

从目前初中数学教学的现状来看，多数老师的教学是学生做大量的题目，教师讲大量的题目。学生对一种固定的题目模式较容易掌握，但思维很狭窄，特别是改变已知条件，变换了图形位置后就一愁莫展，束手无策，脑子里只记住一些公理、定理或者定义，但是叙述不清楚，每步的依据说不上来，几何逻辑推理能力和逻辑思维能力较弱。这些促使我们思考：如何提高学生的数学学习兴趣，如何提高数学课堂的有效性？笔者通过平时的教学实践发现，反复进行的一题多变的训练，是帮助学生克服思维狭窄性的有效方法。

一、一题多变的定义

一题多变是指从多角度、多方位对例题进行变化，引出一系列与本例题相关的题目，形成多变导向，使知识进一步精化的教学方法，在复习课和习题课教学中一题多变就是要围绕数学问题或例题中所需反映的数学实质进行一系列的问题变化，使学生在一题多变的训练中得以掌握知识本质并从中提高发现问题、提出问题、分析问题与解决问题的能力，不局限于问题的某一方面，能够随机应变，举一反三，触类旁通，进而减轻学生学业负担，培养学生的创新能力。

二、一题多变的作用

在平时的数学教学过程中，恰当的变更问题情境或改变思维角度，培养学生的应变能力，引导学生从不同途径寻求解决问题的方法。通过多问、多思、多用等激发学生思维的积极性和深刻性。下面本人结合理论学习和数学课堂教学的实践，谈谈在数学教学中如何进行变式训练培养学生的思维能力。

1.一题多变，加深概念理解 新课中，从培养学生思维能力的要求来看，形成数学概念，提示其内涵与外延，比数学概念的定义本身更重要。在形成概念的过程中，可以利用变式引导学生积极参与形成概念的全过程；在公式、定理的教学中，关键是明确理解定理和公式中概念的联系，通过变式训练，培养学生辨析定理和公式的能力。

为了加深一次函数和正比例函数的区别和联系，我们还可以做如下的变形：

2.一题多变，深挖习题结论 牛顿说过：“没有大胆的猜想就做不出伟大的发现。”中学生的想象力丰富，因此，在习题课教学中要善于对习题进行必要的挖掘。通过对习题的结论进行变换，对同一个问题从多个角度来研究。这种训练可以增强学生解题的应变能力，培养学生的创造性思维和发散性思维。

例2：如图1，△ABD和△BCE都是等边三角形，且点A、B、C在一条直线上，比较AE与DC的大小。你能对所得结论说明理由吗？

本题主要是利用等边三角形的性质，全等三角形的性质及判定来进行证明、求解。本问对于学生来说，没有障碍，由等边三角形性质自然联想到三条边相等、三个角相等，构建△ABE≌△DBC的过程中，边的相等学生可以轻松的从等边三角形得出，而对于等角加等角得到角相等，是解决三角形全等的关键。如果问题就此结束就会显得题目过于单一，所以教师可对题目加以补充、启发，完善本题结论和证明。

思路一：从相等的线段这一角度出发，可得如下结论：

①AD＝BD＝AB②BE＝CE＝BC③AE＝CD④AG＝DF⑤BG＝BF⑥EG＝CF

思路二：从相等的角这一角度出发，可得如下结论：

①∠DAB＝∠ABD＝∠ADB＝∠EBC＝∠ECB＝∠BEC＝∠DHA＝∠EHC＝∠DBE＝600

②∠AHB＝∠CHB③∠ABE＝∠DBC＝1200④∠AEB＝∠DCB⑤∠EAB＝∠CDB＝∠ECD

⑥∠AGB＝∠DFB⑦∠EGB＝∠CFB

思路三：从全等三角形这一角度出发，可得如下结论：

①BC②ΔAGB≅ΔDFB③ΔABC

思路与解法四：从平行线这一角度出发，可得如下结论：

①GF∥AC②BD∥CE③AD∥BE

思路与解法五：从相似三角形这一角度出发，可得如下结论：

①△DGH∽△AGB②△HFE∽△BFC③△DFB∽△CFE

④△CBF∽△CAD⑤△HGF∽△HAC∽△GDF∽△BDC∽△BAE

本例在条件没有改变的情况下对结论发散性地分析，在分析过程中蕴含着异常丰富的思维和推断过程，如此便能很好地锻炼观察、猜想、推断、验证等探求能力和有效地发展创造性思维能力。

3.一题多变，回归基本图形 数学题目是做不完的，我们要提高学习效率，就不能就题论题，初中几何中有许多基本图形，这些基本图形与其它知识点组合在一起，共同演绎着变化无穷的几何综合性问题.解决这类问题，一般要分离或者构造出基本图形，然后应用基本图形的性质及相关结论解决问题。

类型1 “K”字型全等基本图形：.如图3，已知AB＝AC，AB⊥AC，DE过点A，且CD⊥DE，BE⊥DE，垂足分别为D、E，则△ADC≌△BEA

例3、如图4，平面直角坐标系中，已知直线y＝x上一点P（2，m），C（0，n）为y轴上一点，以P为直角顶点作等腰Rt△PCD，过点D作直线AB⊥x轴，垂足为B，直线AB与直线y＝x交于点A.判断线段OB和OC的数量关系，并证明你的结论；

解析：OB＝OC理由如下：过点P作MN⊥OC交OC于M，交AB于N，

∵∠CMP＝∠DNP＝∠CPD＝90°，∴∠MCP＋∠CPM＝∠MPC＋∠DPN＝90°，

∴∠MCP＝∠DPN，∵将点 P（2，m）代入 y＝x，得 m＝2，

∴P（2，2），∴OM＝BN＝2，PM＝2，∵等腰 Rt△CDP中，PC＝PD，

∴△MCP≌△NPD，∴DN＝PM，PN＝CM，又∵点P在直线y＝x上，

∴OM＝PM，∴OM＋CM＝PM＋PN，∴OC＝MN，又∵MN＝OB，∴OB＝OC；

类型二 “K”字型相似基本图形，如图5，B，C，E三点共线，∠B＝∠ACD＝∠E＝90°.则△ABC∽△CED.

例4、如图6，已知矩形ABCD的顶点A，D分别落在x轴、y轴上，OD＝2OA＝6，AD：AB＝3：1，则点 C的坐标是_____

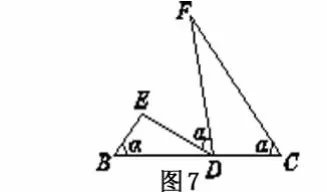
“K”字型相似基本图形（2）如图7，B，D，C三点共线，∠B＝∠EDF＝∠C＝∠α.则△BDE∽△CFD.

这样通过一题多变培养学生寻找共性，克服困难的信心，数学问题的解决过程亦是如此，将复杂问题简单化，一步步将未知问题转化到已知范围.在求解几何问题时，就是要通过观察、类比、联想，把复杂图形转化为简单的基本图形问题，就能容易获解。通过这种训练，不仅使学生更深入地掌握了知识，还可预防思维定势，同时也培养了发散思维能力.

三、感悟

知识是静态的，思维是活动的；例、习题是固定的，而它的变化却是无穷的。在数学教学中，教师一定要充分利用“一题多变、多题归一”的方法，将一题演变成多题，而题目实质不变，让学生解答这样的问题，能随时根据变化的情况思考，从中找出它们之间的区别和联系，以及特殊和一般的关系.使学生不仅能复习、回顾、综合应用所学的知识，而且使学生把所学的知识、技能、方法、技巧学牢、学活，培养思维的灵活性和解决问题的应变能力。