高速铁路线路中断条件下列车开行方案研究
林 立,孟学雷,宋仲仲
(兰州交通大学 交通运输学院,甘肃 兰州 730070)
0 引言
近年来我国高速铁路发展迅速,其线网具有点多、线长、面广的特点,路基、桥梁、涵洞、隧道等高速铁路设施均容易遭受自然灾害的影响;此外,各类高速铁路运输事故及社会安全事件也偶有发生。这些情况均会导致高速铁路线路中断,无法使列车正常运营,因而铁路部门需要做出应急预案从而保证运输任务的完成。列车开行方案是铁路运输组织的核心,针对高速铁路线路中断条件下列车开行方案的研究可以为铁路部门提供应急决策依据,更加灵活快速地疏散旅客。
现阶段有关列车开行方案的研究大都是基于正常运行条件的[1-4],而在应急条件下的相关研究较少。王莉等[5]在分析突发事件下行车组织相关特点的基础上,建立旅客列车行车组织双层规划模型,并以京沪高速铁路为例进行验证分析;吴晓东等[6]构建了特殊需求下的铁路运输组织模型,对突发事件下列车运行计划的调整问题进行研究;Meng等[7]重点考虑了应急条件下列车发车频率和停站方案;文超等[8]分析了列车运行冲突管理的现状,并对我国高速铁路线路中断存在的问题进行研究;谢正媛[9]以旅客周转量最大为优化目标,探讨了大面积雪灾对铁路弹性通过能力和列车开行方案的影响;陈彩霞[10]着眼于最大化旅客周转速度,建立事故灾害条件下高速铁路列车开行方案模型,并设定虚拟场景进行求解;孟学雷[11]通过考虑列车径路和运行调整等具体问题,构建双层规划模型对突发事件下的列车运输组织方法进行研究;王莉等[12]分析了不同等级的铁路突发事件下运输组织的复杂性及差异性,并阐明了不同运输组织方式间的关联性;李望等[13]通过定性分析与定量计算,探讨了列车运行的效率和安全问题,给出了列车运行时的最优规则;王卓等[14]通过对 2 种行车事故预测方法进行仿真分析,比较 2 种预测方法具有不同的适用性。这些研究针对突发事件下列车的开行方案时均未考虑动车组数量及旅行时间的限制[7,9-10]。因此,在谢正媛[9]和陈彩霞[10]研究的基础上对线路突发情况中断条件下目标函数和约束条件加以改进,考虑旅客出行时间和动车组车底数量限制,进而建立城际列车开行方案优化模型,并且设计模拟退火算法进行求解。
1 高速铁路线路中断条件下列车开行方案问题分析
1.1 问题描述
假设 2 座城市间有 2 种不同等级的线路,可选线路集合l={lg,lc},其中lg为高速线路,lc为城际线路;车站集合S={S1,S2,…,Sn};列车种类集合T={D,G},其中D为动车组列车,G为高速动车组列车,正常条件下D类列车在城际线路上运行,G类列车在高速线路上运行,突发事件下允许列车在不同的线路上运行以满足旅客运输任务;列车集合U= {T1,T2,…,Tu}。
假设高速线路发生中断并且短时间内难以恢复,则G类列车需要在城际线路上运行,即高速线路上的客流需要转移至城际线路上。一般而言,2 条线路即使所经车站不同而所在枢纽与原车站枢纽相同,为便于描述,假设 2 条线路所经车站均相同。
1.2 旅客出行时间影响分析
根据既有研究[11],在确定突发事件下列车新的运行径路时,设计了最大容忍延展系数,以避免列车新径路绕行距离过长造成严重晚点的情况发生。在这样的情况下,当高速线路中断造成G类列车在低等级的城际线路上运行时,由于线路条件的限制,G类列车在城际线路上需要采取降速运行的方法,则必将导致旅客出行时间的增加。对于时间价值较高的高速铁路客流而言,其对旅行时间的延长也有一定的容忍范围。例如,正常情况下 A,B 两地间乘坐高速铁路的出行时间为 60 min,高速铁路线路因故发生中断,高速铁路列车需要在城际线路上降速运行,如果旅客对出行时间延长的容忍系数为 1.5,则高速铁路列车在城际线路上从 A 到 B 的旅行时间应不超过 90 min。当运行速度受限无法提高时,为了避免旅行时间过长,可以通过采取减少停站的方法来提高旅行速度。
tc为G类列车在城际线路上的旅行时间,tg为G类列车在高速线路上的旅行时间,β为旅客对出行时间延长的最大容忍系数,则根据上述分析,tc需满足以下条件。

2 高速铁路线路中断条件下列车开行方案模型构建
2.1 目标函数
正常运营条件下编制列车开行方案时,目标函数主要从以下 2 个方面进行阐述,即旅客出行费用及时间成本最小,铁路运输部门效益最大。而当发生线路中断等较为严重的事故时,尽快疏散旅客应作为优化目标。
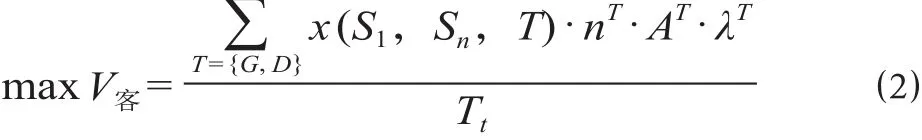
式中:V客为旅客疏散速度,即单位时间内运输的旅客人数;x(S1,Sn,T) 为 0-1 变量,x(S1,Sn,T) = 1 为城际线路上从车站S1到Sn开行T类列车,x(S1,Sn,T) = 0 为从车站S1到Sn不开行T类列车;nT为T类列车的开行数量;AT为T类列车的定员;λT为T类列车的满载率,通常情况下,为了提高旅客出行舒适度,满载率取 0.7~0.8,而在铁路应急条件下,可以适当提高满载率的取值以实现客运周转的需要;Tt为所有列车总旅行时间之和。式中:Tr为列车总运行时间之和;Ts为所有列车的总停站时间消耗;dS1Sn为城际线路上从车站S1到Sn的里程;vT为T类列车的平均运行速度;ts为包括列车起停车附加时分在内的简化的额定停站时间消耗,为便于计算,假设所有列车停站时间消耗都相同;Sm为中间站,为 0-1 变量,如果列车Tu在车站Sm停车则= 1,否则= 0。

2.2 约束条件
(1)线路通过能力约束。在列车运营时段内,所开行的列车数量之和不超过该线路的通过能力,计算公式为

式中:Nc为城际线路的通过能力。
(2)车站通过能力约束。经过车站Si的列车数量之和不应超过车站通过能力的限制,计算公式为

式中:CSi为车站Si的通过能力。

(3)动车组数量约束。制订列车开行方案时不能无限制地使用动车组,而应使其限制在可用动车组数量范围内,计算公式为式中:nD为D类列车的开行数量,nG为G类列车的开行数量;H为列车运营时段;hD和hG分别为D类列车和G类列车的周转时间;mD和mG分别为D类列车和G类列车的可用动车组数量。

(4)客流需求满足约束。OD 对 (Si,Sj) 间开行的所有列车的载客能力要满足此 OD 对间的客流需求,计算公式为式中:x(Si,Sj,Tu) 为 0-1 变量,x(Si,Sj,Tu) = 1为列车Tu服务于 OD 对 (Si,Sj) 间的客流,即列车Tu在线路上Si和Sj站均停车,否则x(Si,Sj,Tu) = 0;ATu为列车Tu的定员;λTu为列车Tu的满载率;q(Si,Sj) 为从Si到Sj的客流需求量。
(5)旅客出行时间约束。根据对旅客出行时间所受影响的分析,每一列G类列车在城际线路上的旅行时间不应超过由容忍系数所确定的旅行时间的上限,计算公式为

式中:vG为线路中断条件下G类列车在城际线路上运行时的平均速度;tG为在正常运营条件下,G类列车在高速线路上从S1到Sn的平均旅行时间;β为G类列车在城际线路上运行时,旅客对出行时间的最大容忍系数。
(6)列车停站约束。每一列车在运行径路两端的车站都必须停车,计算公式为
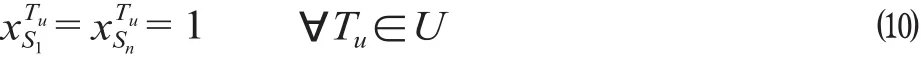
(7)决策变量约束。列车开行数量的取值应该为非负整数,计算公式为

3 高速铁路线路中断条件下列车开行方案求解算法
经分析,所构建模型为非线性整数规划模型,利用现有的求解软件求解较为困难,因而采用模拟退火算法求解上述模型。
3.1 初始解的构造
(1)随机生成满足约束式 ⑷~⑺、⑾ 的D类列车和G类列车的开行数量。
(2)D类列车初始停站方案均为站站停,由约束式 ⑼ 可得G类列车在城际线路上运行时的最大停站次数,据此随机生成G类列车的停站方案,使其总停站次数与最大停站次数相等;结合约束式 ⑽,确定每一列车的停站方案。
(3)根据上述生成的停站方案,确定出所有服务于 OD 对 (Si,Sj) 间的列车数量,即在Si和Sj均停站的列车。由此判断其是否满足约束式 ⑻,如果满足,则将此解作为列车开行方案的初始解;否则,随机调整列车的开行数量和停站方案,直至出现可行解。
3.2 模拟退火算法步骤
模拟退火算法步骤如下。
步骤 1:初始化。基础参数设定,初始温度T0,令当前温度T=T0,终止温度为Tend,每个温度T时的迭代次数为L,温度下降比例为Ψ,令l= 1,m= 0。
步骤 2:初始解的生成。按照初始解的构造方法确定初始解N0,令当前解N1=N0。
步骤 3:邻域解的生成。随机生成满足约束式⑷~⑺、⑾ 的D类列车和G类列车的开行数量并随机生成满足约束式 ⑽ 的列车停站方案,由此可以产生新解N2。
步骤 4:判断新解是否满足约束。根据列车停站方案确定出服务于 OD 对 (Si,Sj) 的列车数量和每列车的停站次数,由此可判断新解N2是否满足约束式 ⑻~⑼,如果满足则转步骤 5,否则转步骤 7。
步骤 5:计算目标函数值及其增量。根据公式 ⑵ 计算f(N1) 和f(N2),并计算目标函数值的增量Δf=f(N2)-f(N1)。
步骤 6:根据 Metropolis 准则判断是否接受新解N2。如果 Δf>0,则接受新解N2,即N1=N2;否则计算新解的接受概率 exp (Δf/T),生成 (0,1) 区间上均匀分布的随机数η,如果满足 exp (Δf/T)>η,也接受新解N2,即N1=N2;否则,保留当前解N1。
步骤 7:令l=l+ 1,如果l≤L,则转步骤 3,否则转步骤 8。
步骤 8:降温。令Tm+1=ΨTm,T=Tm+1,m=m+ 1。
步骤 9:算法终止检验。如果T<Tend,结束程序,输出当前解N1;否则令l= 1,转步骤 3。
4 算例分析
4.1 基础数据
以某地区高速铁路线路为例进行实例分析,高速铁路线路及区间里程示意图如图1 所示。正常运营条件下,D类列车、G类列车分别在城际线路和高速线路上运行;假设高速线路因事故灾害发生中断并且短时间内难以恢复,G类列车和D类列车均在城际线路上开行;由于旅客列车大都是成对开行的,因而仅考虑研究一个方向上开行方案的制订,即 A→E 方向;高速铁路线路中断条件下,各城市间某日OD 客流数据如表1 所示。
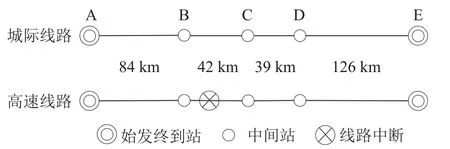
图1 高速铁路线路及区间里程示意图Fig.1 Diagram of the line and section mileage
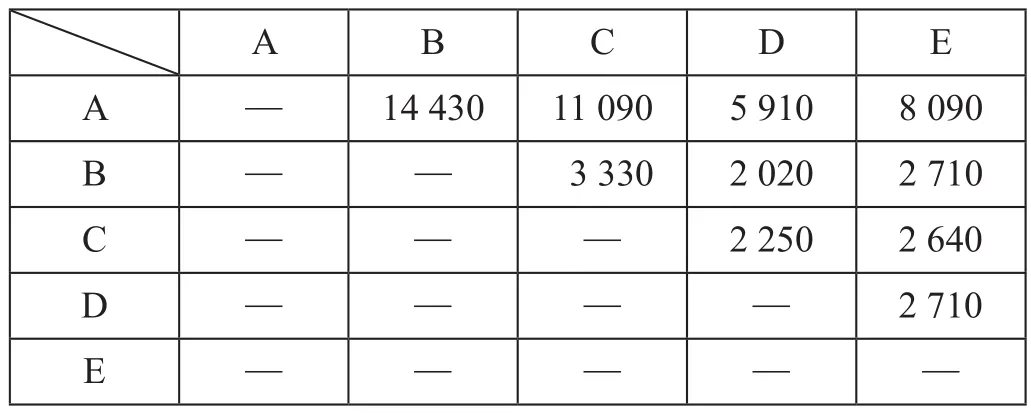
表1 高速铁路线路中断条件下某日OD 客流数据Tab.1 OD passenger fl ow under the condition of high-speed railway interruption
由于高速铁路线路里程较短,列车所经车站较少,因而旅行时间相对较短,将G类列车在城际线路上降速运行时的旅客出行时间容忍系数设为 1.3[11],城际线路上 A→E 方向通过能力为130 列[3,11-12],列车运营时段取 16 h。G类列车和D类列车的其他参数取值如表2 所示。
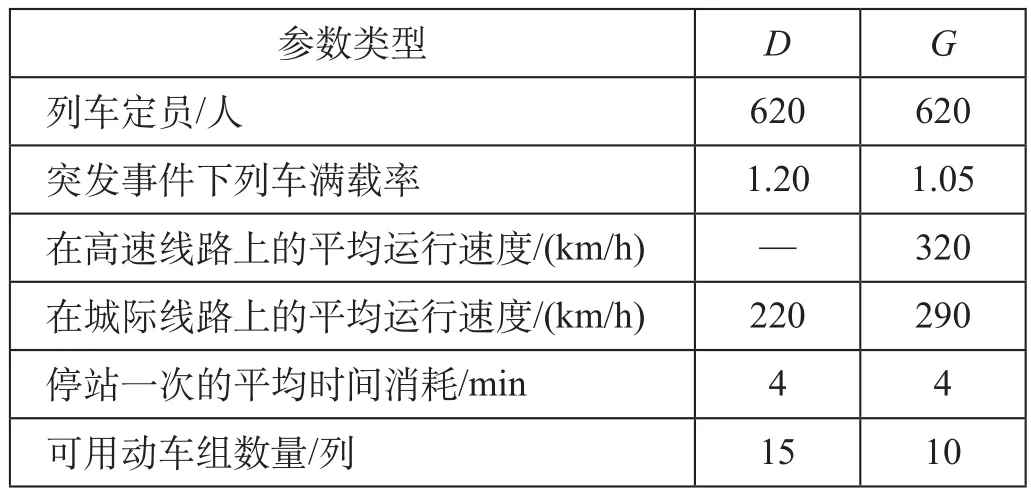
表2 列车参数取值Tab.2 Train-related parameters
4.2 算例结果
采用 Matlab 编程实现算法,初始温度T0= 106,终止温度Tend= 10-6,迭代链长L= 10,温度下降比例Ψ= 0.95。最大迭代次数为 539 代,迭代过程如图2 所示,当迭代到 341 代后目标函数值达到最大且趋于稳定,此时目标函数值为 540.3,开行D类列车 38 列,G类列车 44 列,列车开行方案计算结果如图3 所示。
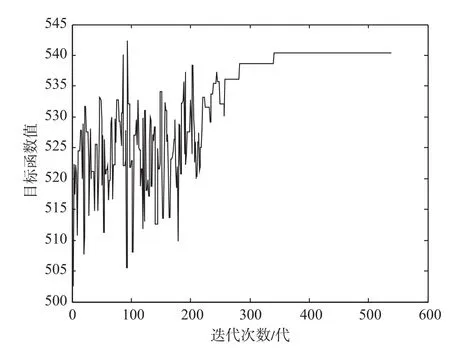
图2 迭代过程图Fig.2 Iterative process diagram
4.3 结果分析
由G类列车在城际线路上降速运行时的旅客出行时间容忍系数为 1.3 可得,列车在中间站的最

图3 列车开行方案计算结果Fig.3 Calculation results of train operation plan
大停站次数为 2,因而没有站站停的G类列车;G类列车比D类列车开行数量略多,保证了在突发事件下旅客的疏散速度;所有G类列车的总停站次数为 51,D类列车的总停站次数为 64,G类列车总停站次数较少也保证了旅行速度较高;既有 OD 客流总需求为 55 180,所求列车开行方案总运能为56 916,在保证 OD 客流需求的同时使列车虚糜度较低,说明了所求的解较优。
5 结论
针对高速铁路线路中断条件下的列车开行方案的编制问题,构建以最大化旅客疏散速度为目标的优化模型,并且设计了模拟退火算法进行求解,主要结论如下。
(1)在模型中考虑旅客出行时间的影响,将G类列车在城际线路上降速运行后的旅行时间限制在一定范围内;同时把动车组运用数引入到约束中,使开行方案中所用动车组数量不至过高。
(2)利用文中所构建的模型求解列车开行方案,可以在尽快疏散旅客的同时,使列车的运能虚糜度较低。
(3)研究了局部线路列车开行方案问题。实际上,某条高速铁路线路发生事故后会对与其相关联的其他线路造成不同程度的影响;同时,开行方案与客流具有相互影响的关系,而非单纯地由客流决定开行方案,旅客的换乘行为亦会对开行方案造成一定的影响,应深入研究和解决这些问题。

