组合载荷作用下平盖双开孔接管结构强度性能分析

， ， ，

(1.江苏省特种设备安全监督检验研究院 泰州分院， 江苏 泰州 225306；2.中国特种设备检测研究院， 北京 100083；3.南京工业大学 机械与动力工程学院， 江苏 南京 211800)

平盖双开孔接管结构在石油、化工和能源行业中的板壳式热交换器中有着广泛的应用。由于平盖开孔接管区存在结构不连续，接管区应力的分布比较复杂，导致局部应力集中，加之平盖接管外载荷的耦合作用，如接管弯矩、轴向力、扭矩，使得平盖双开孔结构应力分布更加复杂。因此，对平盖双开孔结构的应力分布规律进行研究就显得尤为重要。关于接管载荷的研究，国外学者Bijlaard[1]早在1955年就提出了圆筒形容器在接管外载荷作用下的应力计算方法。1984年，Meshon J L等人[2]通过对圆筒形容器在接管外载荷作用下的局部应力研究对WRC107公告进行了补充。2001年，Aleksandar Petrovic[3]在对接管端部施加外载荷情况下，研究了压力容器的应力分布情况。

国内学者对圆筒形容器在接管外载荷作用下的应力分布规律进行了大量研究。桑芝富等人[4-5]采用实验的方法研究了接管轴向推力作用下圆筒开孔接管结构的应力分布，并对接管弯矩作用下压力容器开孔接管局部应力进行研究。吴本华等[6]研究了接管弯矩作用下容器开孔结构弹性应力。唐清辉等[7-9]研究了接管轴向载荷和内压共同作用对筒体强度性能的影响，同时还研究了接管弯矩和内压作用下接管区的弹性应力分布和极限载荷分布规律。徐心怡等[10]采用应力分析法和极限载荷分析法研究了在内压和支管外力矩作用下的圆柱壳径向开孔接管。张小平等[11]采用有限元分析方法获得轴向和环向双开孔-接管结构的应力集中系数分布图。任智杰[12]通过实例分析了作用在接管端面上的轴向外力对承受内压的压力容器接管部位的强度计算结果的影响。左春梅等[13]通过有限元分析很好地解决了接管承受复杂外载荷情况下的应力计算。郭崇志等[14]对封闭式开孔接管问题进行了分析设计方法研究，并推导出了结构的求解方程。

以上国内外文献研究的一个共同点是圆筒上接管外载荷对接管区的应力影响，而针对平盖双开孔接管结构在接管外载荷和内压共同作用下的应力分布研究则一直很少。为此，笔者通过有限元方法，研究了平盖双开孔接管结构在接管轴向力与内压共同作用下的应力分布规律，其结果可为组合载荷作用下的平盖双开孔接管结构强度设计提供参考。

1 平盖双开孔接管结构尺寸及参数

某板壳式热交换器中的平盖双开孔接管结构示意图见图1。图1中，D为筒体外径，δ1为筒体壁厚，δ2为平盖厚度，L为接管N1、N2之间的中心距离，d0为接管外径，δ0为接管的壁厚，mm。

本例中，D=340 mm，δ1=12 mm，δ2=30 mm，L=160 mm，d0=60 mm，δ0=6 mm。

图1 平盖双开孔接管结构示图

平盖双开孔结构的设计压力2.5 MPa，设计温度150 ℃。筒体和平盖结构的材质为Q235B，接管材质20钢，各部件材料力学性能见表1。

表1 平盖双开孔接管结构部件材料力学性能

2 平盖双开孔接管结构有限元分析

2.1 有限元计算工况

平盖双开孔接管结构除了承受设计压力p外，在接管端面处会承受轴向力F的作用。根据轴向力F作用方向的不同，可分为轴向推力F1和轴向拉力F2。考虑不同组合载荷作用下轴向力对整体结构性能的影响，设置了4种计算工况，见表2。

表2 平盖双开孔接管结构计算工况

表2中，工况1表示整体结构仅承受内压，接管N1、N2处无轴向力作用；工况2为受内压作用的同时，轴向推力同时作用于接管N1和N2；工况3为受内压作用的同时，轴向拉力同时作用于接管N1和N2；工况4为受内压作用的同时，轴向推力作用于接管N1，轴向拉力作用于接管N2。

2.2 有限元模型网格划分及边界条件

鉴于平盖双开孔结构的对称性，以平盖、接管N1、N2和部分筒体的1/2进行有限元建模。

选取Solid185实体单元对平盖、接管、筒体各部件进行六面体网格划分，得到的平盖双开孔接管结构有限元模型见图2。

图2 平盖双开孔接管结构有限元模型

对于平盖双开孔接管结构载荷及边界条件，在筒体、平盖、接管承压内表面施加设计压力p。针对不同工况，在接管N1和N2端面施加轴向推力F1或轴向拉力F2，在对称面施加对称约束。在筒体端面施加全约束。

2.3 计算结果分析

4种计算工况下平盖双开孔接管整体结构应力云图见图3。

从图3可知，①平盖双开孔不连续结构表现出了明显的应力集中。由于双开孔不连续的交互作用， 使得两接管之间平盖部分为高应力区。②仅在内压作用下，工况1的最大应力点位于接管N1与平盖相连接的内表面，最大应力值为109.6 MPa。③在内压和接管轴向推力的作用下，工况2的最大应力点位于筒体与平盖相连处的内表面，最大应力值相比工况1下降，为62 MPa。④在内压和接管轴向拉力的作用下，工况3的最大应力点位置与工况1一致，但最大应力值相比工况1上升，为196.7 MPa。⑤轴向推力作用于接管N1，轴向拉力作用于接管N2，工况4中最大应力点位于接管N2与平盖相连内表面，最大应力值为149.2 MPa。

图3 4种计算工况下平盖双开孔整体结构应力云图

根据JB 4732—1995(2005年确认)《钢制压力容器——分析设计标准》[15]中的应力分类方法，将应力分为一次总体薄膜应力Pm、一次局部薄膜应力PL、一次弯曲应力Pb、二次应力Q和峰值应力F，并根据不同的组合对应力进行评定。根据有限元计算结果，沿最大应力点处提取4种工况下的局部薄膜应力、一次加二次弯曲应力，平盖双开孔接管结构危险点、应力评定结果见表3。

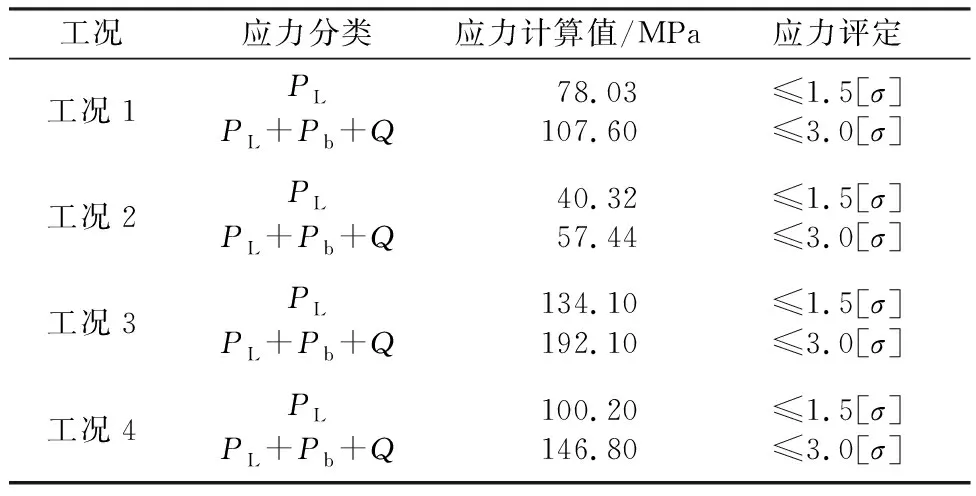
表3 不同工况下平盖双开孔结构危险点应力评定结果

从表3所示的应力评定结果来看，4种工况下应力值均满足评定要求且具有较大的安全裕量。比较4种工况下的应力值，工况2的局部薄膜应力和一次加二次弯曲应力值最小，工况3 的局部薄膜应力和一次加二次弯曲应力值最大。相比工况1仅受内压作用时的应力值，在双接管轴向推力和内压共同作用下，接管与平盖不连续处的应力集中有效降低，从而应力值减小。而在双接管轴向拉力和内压共同作用下，接管与平盖不连续处的应力集中显著加剧，应力值明显增大。对于工况4，轴向推力减缓了接管N1与平盖相交处的应力集中，但轴向拉力加剧了接管N2与平盖相交处的应力集中。

以上模拟计算结果表明，接管轴向推力使平盖开孔接管区弹性应力变小，提高了平盖开孔接管区的承载能力。而接管轴向拉力使平盖开孔接管区弹性应力变大，应力集中程度提高，降低了平盖开孔接管区的承载能力。这种规律是在给定的轴向拉力和推力条件下得出的，当接管上轴向推力或拉力逐渐增大时，平盖双开孔接管结构各部件的应力水平随组合载荷的变化规律，还有必要作进一步详细分析。

3 不同组合载荷对平盖双开孔接管结构应力分布的影响

设计压力p=2.5 MPa恒定，组合载荷的变化是根据轴向力的大小来决定，取轴向推力和轴向拉力的数值为5～35 kN，每5 kN单调增加。

根据JB 4732—1995中的应力分类，以接管、平盖、筒体各部件的最大应力点进行线性化处理，提取各部件的局部薄膜应力SⅡ和一次加二次应力SⅣ，详细分析平盖双开孔结构各部件在不同组合载荷变化下的应力分布规律。

3.1 轴向推力F1变化

在内压p和轴向推力F1作用下，平盖双开孔接管结构各部件的局部薄膜应力SⅡ和一次加二次应力SⅣ分布规律分别见图4和图5。

图4 p+F1变化下平盖双开孔结构3个零件的局部薄膜应力SⅡ

图5 p+F1变化下平盖双开孔结构3个零件的一次加二次应力SⅣ

从图4和图5中可知，①接管、 平盖、筒体上的局部薄膜应力和一次加二次应力变化基本一致。②内压恒定，随着轴向推力的逐渐增大，各部件的应力变化均呈现先减小后增大的趋势。③接管轴向推力可以使平盖双开孔结构的弹性应力变小，提高结构的承载能力，在轴向推力F1=15 kN附近，弹性应力最小，平盖双开孔结构的承载能力达到最佳。④随着轴向推力变大，各部件的应力反而增大，表明较大的轴向推力反而降低了平盖双开孔结构的承载能力。

3.2 轴向拉力F2变化

在内压p和轴向拉力F2作用下，平盖双开孔接管结构各部件的局部薄膜应力SⅡ和一次加二次应力SⅣ分布规律分别见图6和图7。

从图6、图7可知，随着轴向拉力的增大，平盖双开孔结构各部件的应力均呈现增大的趋势。接管和筒体的应力随轴向拉力增加呈现线性增加，平盖上的应力增幅较为平缓，接管上的应力增幅度最大。以上变化规律表明，轴向拉力的增大，使得各部件的应力值增大，降低了平盖双开孔结构的承载能力。

图6 p+F2变化下平盖双开孔3个零件的局部薄膜应力SⅡ

图7 p+F2变化下平盖双开孔结构3个零件的一次加二次应力SⅣ

3.3 轴向推力F1和轴向拉力F2变化

在内压p和轴向推力F1及轴向拉力F2作用下，平盖双开孔接管结构各部件的局部薄膜应力SⅡ和一次加二次应力SⅣ分布规律分别见图8和图9。

图8 p+F1+F2变化下平盖双开孔结构3个零件的局部薄膜应力SⅡ

图9 p+F1+F2变化下平盖双开孔结构3个零件的一次加二次应力SⅣ

从图8、图9可知，各部件的应力变化趋势与组合载荷p+F2的变化规律基本一致，随着轴向推力和轴向拉力的增加，接管、平盖和筒体上的应力均呈现单调增大的趋势。不同的是，各部件的应力值相对较小，其原因是接管N1受轴向推力，接管N2受轴向拉力，轴向推力和轴向拉力共同作用所致。

4 结论

(1)采用有限元法对组合载荷作用下的平盖双开孔结构进行分析，对4种工况下的平盖双开孔结构强度进行应力评定，评定结果表明，4种工况下应力值均满足评定要求且具有较大的安全裕量。

(2)内压和轴向推力作用下的平盖双开孔结构，当轴向推力F1<15 kN时，轴向推力的增加可以提高平盖双开孔结构的承载能力，当轴向推力F1>15 kN时，轴向推力的增加反而降低平盖双开孔结构的承载能力。

(3)内压和轴向拉力作用下的平盖双开孔结构，轴向拉力会使结构应力增大，显著降低平盖双开孔结构的承载能力。而在内压和轴向拉力及轴向推力的共同作用下，平盖双开孔结构承载能力会下降，但相比内压和轴向拉力作用下较小。