储罐大脚焊缝裂纹裂尖应力强度因子研究
, , ,
(中石化管道储运有限公司, 江苏 徐州 221008)
进行大脚焊缝焊接时,由于焊接技术或焊接设备等原因,会出现一些焊接缺陷,在腐蚀介质不断侵蚀下,缺陷将不断扩展,包括焊缝上的小尺寸凹坑和短裂纹、焊缝与底板连接处的咬边或未熔合导致的短裂纹和长裂纹、底板上在大角焊缝附近热影响区的长裂纹等。随着储罐的大型化,计算其底板、罐壁以及大角焊缝处应力的更精确方法不断出现[1-5],这为对大角焊缝处裂纹缺陷进行精准的断裂分析奠定基础。在对T型焊趾表面裂纹断裂性能的不断探索过程中,也出现了可用于工程实际的焊趾放大系数Mk[6-13],且Bowness D的焊趾放大系数表达式已经被英国规范BS7910采用,GB/T 19624—2004《在用含缺陷压力容器安全评定》[14]中也给出了计算焊趾裂纹应力强度因子K1的焊趾放大系数的取值表格。
大脚焊缝处是储罐在静压作用下应力水平最高的位置,出现在该位置的裂纹是最危险的,所以研究焊缝裂纹缺陷的断裂性能至关重要。
文中首先对储罐进行静力分析,根据底板的位移和变形,得到建模方便且计算量较小的简化储罐有限元模型,并在储罐简化模型的基础上,建立了多组焊缝缺陷,进行大量的数值模拟,获得不同位置、不同尺寸的裂纹最深处的应力强度因子数值变化规律,并与Bowness D和GB/T 19624—2004的计算结果进行对比,为焊缝缺陷的检测及剩余强度评估提供指导意见。
1 简化储罐模型
1.1 储罐参数
文中所选取的储罐原型是中石化大榭岛油库扩建改造工程的6×100 000 m3大型原油储罐,主体材料为08MnVR钢板,钢材弹性模量E=2.06×105MPa、泊松比υ=0.3、密度ρ=7.85×103kg/m3、屈服应力σs=490 MPa,地基土弹性模量E0=24 MPa、泊松比υ0=0.2。油罐内半径R=40 m,罐壁高H=21.8 m,充水实验高度h=20.2 m,边缘板厚t=20 mm,地基厚度取环梁的高度h0=2.3 m,地基与罐底的摩擦因数μ=0.5。大型原油储罐各层壁板的高度hi以及壁板的厚度ti见表1。

表1 储罐各层壁板尺寸
1.2 弹性地基接触模型及其简化
文献[5]已经验证了地基-底板接触模型的模拟结果更接近于实际值,所以在对二维完整储罐数值模拟时建立接触单元。
在已知储罐底板外边缘部分会翘离地面的情况下,可将几乎无沉降的环梁地基去掉,代之以在底板最外边缘施加竖向位移。经过运算后,提取储罐底板翘离地面位置处界面上的竖向位移9.961 5×10-3m,横向位移为沿截面高度变化的函数:Δx=9.211 8×10-4-0.018 2×(0.02-y),以截面上的位移代替未翘离的底板和地基得到图1所示的简化模型。

图1 二维储罐简化模型
利用简化模型与完整模型计算得到的应力结果对比见图2和图3。由图2和图3看出,底板、罐壁以及大角焊缝处的Von Mises应力分布趋势完全一样,应力值相差不到1%,底板翘离的最大高度与底板边缘滑移的距离相差不到0.2%,所以该简化二维模型完全可以用于代替完整的储罐模型进行有限元分析。

图2 储罐二维完整模型应力计算结果
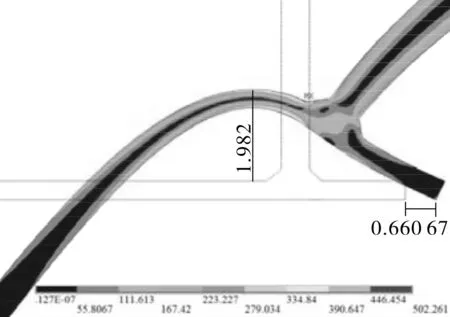
图3 储罐二维简化模型应力计算结果
对不同精细程度的网格划分进行对比,发现当厚度方向、底板的径向、管壁的轴向单元尺寸分别为4 mm、13 mm、25 mm时便能达到精度要求。将二维储罐模型旋转0.5°得到三维储罐模型,并按照上述3个尺寸划分网格,最后得到86 230个单元,普通计算机已能够在较短完成计算任务。
2 应力强度因子理论计算公式
表面裂纹的应力强度因子K1按照以下公式进行计算:
(1)

对于焊趾位置的表面裂纹,则在式(1)中加入焊趾放大系数Mk:
(2)
可根据GB/T 19624—2004中附表D.9和D.10查找Mkm和Mkb的值,也可根据B.FU等给出的公式计算得到[8]。
3 平板裂纹验证
选取与储罐材料相同的0.1 m×0.2 m的平板,在平板横向中心建立深3 mm、长9 mm的半椭圆裂纹,裂纹模型建立方法参考鲁丽君等人[10]的方法,对于裂纹体的网格划分则采取刘刚等[11]、陈景杰等[12]、王永伟等[13]的研究结果提供的意见。在平板底面施加15 MPa的压力,两端施加三向约束,正面施加正对称的边界条件。
利用ANSYS的相互作用积分法计算裂纹最深处的应力强度因子K1,输出20组计算结果,取收敛后波动幅度较小的5组数据的平均值,并与公式计算的理论解对比。平板裂纹的数值模拟结果与理论解对比见图4。

图4 平板裂纹的数值模拟结果与理论解对比
图4中有限元相互积分法计算的结果与理论解吻合良好,说明相互作用积分法适用,网格划分合理。随着裂纹长深比(c/a)的增大,裂纹最深处的应力强度因子值增长趋势逐渐变缓。根据这种现象,便可考虑将一些长度远大于深度的长裂纹作为二维裂纹进行建模求解。
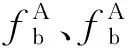
4 焊趾附近裂纹
焊缝对焊趾位置处裂纹的影响,是在薄膜应力和弯曲应力项中分别加入了各自的放大系数来考虑的。但焊缝对与焊趾距离很短的底板裂纹是否有影响也需考虑。首先,在上述简化的三维储罐模型基础上对各位置无缺陷时进行应力线性化分析,得到的薄膜应力和弯曲应力用于公式计算K1值,应力线性化的结果见表2。
以同样的方法和网格划分方式在焊缝附近建立三维裂纹模型。

表2 距焊趾不同距离处的薄膜应力和弯曲应力
4.1 与焊趾不同距离的底板裂纹
与焊趾不同距离裂纹的各方法计算结果对比见图5。当裂纹位置与焊趾距离超过8 mm后,随着裂纹长深比的增加,文献计算的应力强度因子值波动较大,而规范计算的值与有限元模拟的结果越来越接近,且与不考虑Mk的计算结果几乎没有差异。但是当裂纹与焊趾的距离在8 mm之内时,有限元计算的结果却与公式计算的结果有很大差异,主要表现在:①数值模拟的结果普遍高于公式计算的结果。②从距离焊趾很近的位置到焊趾位置,数值模拟的裂纹最深处的应力强度因子值表现为持续增大的趋势,而公式的结果却均是突然下降的趋势。
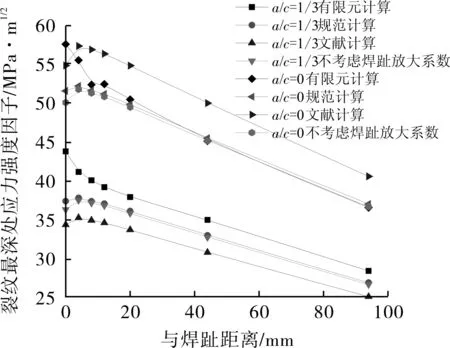
图5 与焊趾不同距离裂纹的各方法计算结果对比
4.2 各深度下与焊趾不同距离的二维裂纹
改变二维裂纹的深度,变化范围为2~8 mm(深厚比为0.1~0.4),各深度下应力强度因子计算结果见图6。同样可以看出,在深度变化时,文献的计算结果仍具有较大的波动性。当裂纹深厚比大于0.2时,规范中焊趾放大系数的取值已经非常接近1,所以不考虑Mk的计算结果与考虑了规范中Mk的计算结果几乎一致。当裂纹与焊趾的距离在8 mm之内时,各深度的裂纹均有着与上述相同的差异。而且当裂纹深度超过5 mm时,这种差异出现在与焊趾更远的距离。这是因为当裂纹深度超过5 mm时,裂纹尖端的塑性区面积扩大,从输出的20组计算结果来看,此时有限元计算的应力强度因子数值的收敛性不再良好,均值得到的结果规律性较差,此时相互作用积分法计算的应力强度因子将不再准确。
观察表2中薄膜和弯曲应力的分布情况,从94 mm的位置到4 mm的位置,薄膜应力变化幅度很小,弯曲应力逐渐增大。但从4 mm的位置到焊趾位置,薄膜应力却突然增加,弯曲应力突然减小,这导致公式计算的焊趾位置的应力强度因子值较小,所以在结构不连续位置,应力线性化得到的薄膜应力和弯曲应力不能直接用于公式计算裂纹的应力强度因子。
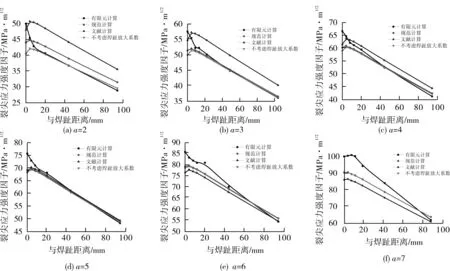
图6 不同深度时二维裂纹应力强度因子计算结果比对
4.3 焊趾位置不同角度的二维裂纹
建立焊趾位置的二维裂纹,取裂纹深度3 mm,裂纹与竖直线的角度为θ,焊趾裂纹应力强度因子随角度的变化数值计算结果见图7。
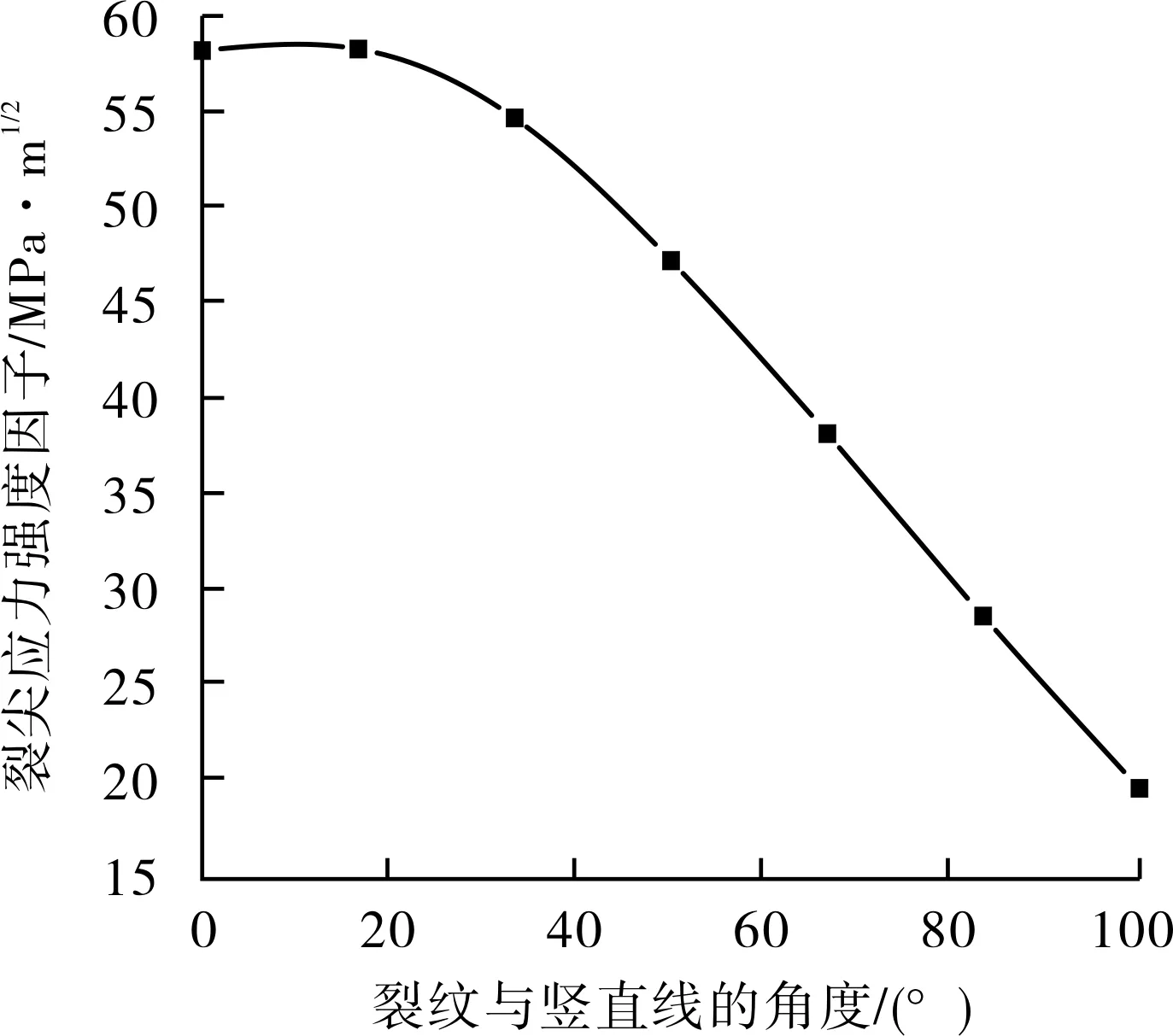
图7 焊趾裂纹应力强度因子随角度的变化
裂纹垂直于底板时,应力强度因子最大,随着与竖直线的夹角逐渐增大,裂纹深度在厚度方向的投影逐渐减小,所以深厚比越来越小,导致裂尖的应力强度因子逐渐减小,且减小趋势呈三角函数形式。
4.4 焊缝上不同角度和位置的三维裂纹
在焊缝上建立深度为2 mm、长度为9 mm的三维短裂纹。当裂纹在焊缝中间位置时,改变厚度方向与竖直线的夹角;当裂纹与竖直线夹角为45°时,改变其与焊趾的位置。数值计算得到的裂纹最深处的应力强度因子随裂纹角度、与焊趾距离的变化趋势见图8。

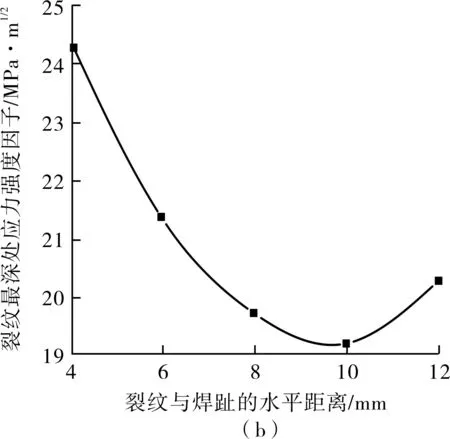
图8 焊缝纵向裂纹最深处应力强度因子随裂纹角度及与焊趾距离的变化趋势
由图8a可知,当裂纹与竖直线夹角为39°左右时,裂纹最深处应力强度因子最大,而此时裂纹与焊缝斜面垂直,所以相同尺寸下,垂直与焊缝斜面的裂纹是最危险的。而图8b大致趋势为越靠近焊趾位置,最深处的应力强度因子越大,这是因为越靠近焊趾应力水平越高。
5 结语
在可代替完整储罐受力的简化模型基础上建立裂纹模型,利用相互作用积分法对焊缝附近的裂纹进行大量的数值模拟,并与规范及文献中的结果进行对比,得到如下结论:①文献[8]中给出的Mk的取值波动性较大,不适用于储罐的大脚焊缝裂纹。 ②当裂纹与焊趾的距离超过12 mm后,计算裂纹的应力强度因子时,可不考虑焊缝的影响;当裂纹与焊趾距离在8 mm之内时,应力线性化的结果不再准确,将导致公式计算的应力强度因子值偏小。③对焊趾处深度大于5 mm的裂纹,由于裂尖塑性区过大,有限元中相互作用积分计算方法将失效。④焊趾附近,无论是底板还是焊缝上的裂纹,当裂纹深度方向垂直于构件表面时,裂纹最深处的应力强度因子最大,且越靠近焊趾位置,其值越大。
根据研究结论,裂纹所在的位置及角度均对裂纹最深处的应力强度因子有很大影响,所以在对裂纹进行检测时,不能仅对裂纹的深度和长度进行检测,还需注重其与焊趾的距离以及与构建表面的角度。
—— 储罐

