水平管蒸发器管外降膜流动数值分析

， ， ，

(1.南京工业大学 机械与动力工程学院， 江苏 南京 211800；2.南京国祺新能源设备有限公司， 江苏 南京 211500)

换热设备作为重要的过程设备之一，在石油化工等行业的热量回收和综合利用中发挥着重要的作用[1]。水平管降膜蒸发器能够有效利用低品位热源，具有传热温差小、总传热系数高、过热区小及不易结垢等优点，在海水淡化以及工业废水处理等领域已经得到了广泛应用[2]。然而，在水平管降膜蒸发器的实际应用中也发现，液膜沿管外壁的分布不够均匀。当局部液膜过薄时，换热管外壁可能会出现干斑现象，而液膜过厚时，换热管外壁的热阻则会增加，这两种情况的出现都不利于管内外介质之间的传热。因此，研究管外液膜厚度的分布规律有助于提高水平管蒸发器的工作效率。

Nusselt[3]忽略液面波动及相界面剪切力的作用，通过理论分析得出液膜厚度的经典计算公式。Gstoehl等[4]利用激光测试技术，以水、乙二醇为介质，测得不同管间距、不同喷淋雷诺数下管外液膜厚度，发现在下半管周Nusselt理论值大于实验值。Wang等[5]对光滑圆管及Turbo-CII管的液膜厚度进行测量，总结出液膜厚度最小值出现在周向角度95°～120°。邱庆刚等[6-7]通过数值模拟研究了管外液膜厚度分布规律，认为管外液膜流经周向角度120°附近时出现最小值，当喷淋密度减小时液膜厚度也减小。朱晓静等[8]分析了液膜流动的瞬态过程，发现液膜厚度在周向角度100°～140°时达到了最小值。

众多学者通过大量实验研究及数值模拟，对液膜厚度沿管周的分布规律达成共识，但对液膜厚度最小值出现的周向位置仍然存在分歧，同时当前研究主要在常温、常压的条件下进行。在实际蒸发环境中，料液的性质会发生变化，对液膜厚度分布也将产生影响。

文中建立二维模型，利用Fluent模拟喷淋密度、管外径及水温对管外降膜流动过程及液膜厚度分布规律的影响，其结果可为水平管降膜蒸发器设计工作提供一定的参考。

1 水平管蒸发器数值模拟

1.1 结构

水平管蒸发器由布液器及水平管束等零部件组成。热流体走水平管管内，可为管外蒸发提供热源。水通过布液器以一定的初速度流出，接触水平管管顶后沿管外壁面以液膜的形式向下流动，在管底汇聚后流向下一排水平管，管外液膜在流动过程中实现蒸发。

水平管蒸发器流体流动示意图见图1，单根管外液膜流动示图见图2。

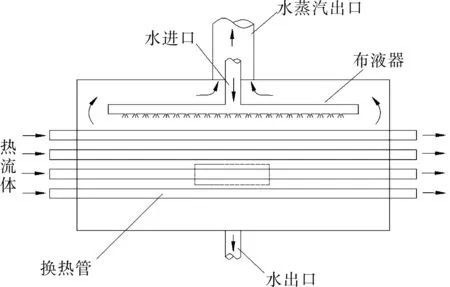
图1 水平管蒸发器流体流动示图

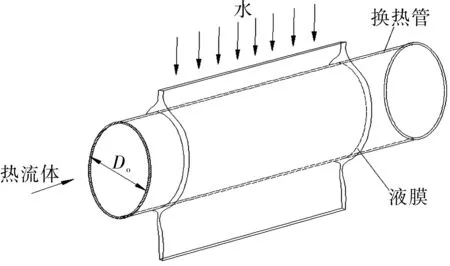
图2 单根管外液膜流动示图

1.2 物理模型

文献[9]认为，沿管轴向不同位置的液膜厚度在同一时刻具有相同的随机分布特性。

以此为据，且考虑圆管对称性，选择喷淋孔中心剖面的一半建立二维对称模型，见图3。图3中，H为布液高度，d为喷淋孔径，Do为管外径，δθ为液膜厚度，mm；θ为自管顶沿顺时针方向取的周向角度，(°)；Γ为喷淋密度，kg/(m·s)。

本例中，H=5 mm，d=2 mm，θ=10°～170°，Do=19～108 mm，Γ=0.12～0.3 kg/(m·s)，其中Do和Γ的具体数值根据研究需要选取。

图3 单根水平管物理模型

1.3 工质物性及基本假设

选择常温、常压条件下水和空气，温度为40 ℃、50 ℃、70 ℃的饱和水及饱和水蒸气作为研究对象，根据文献[10]获得4种工况下工质的物性参数，见表1。

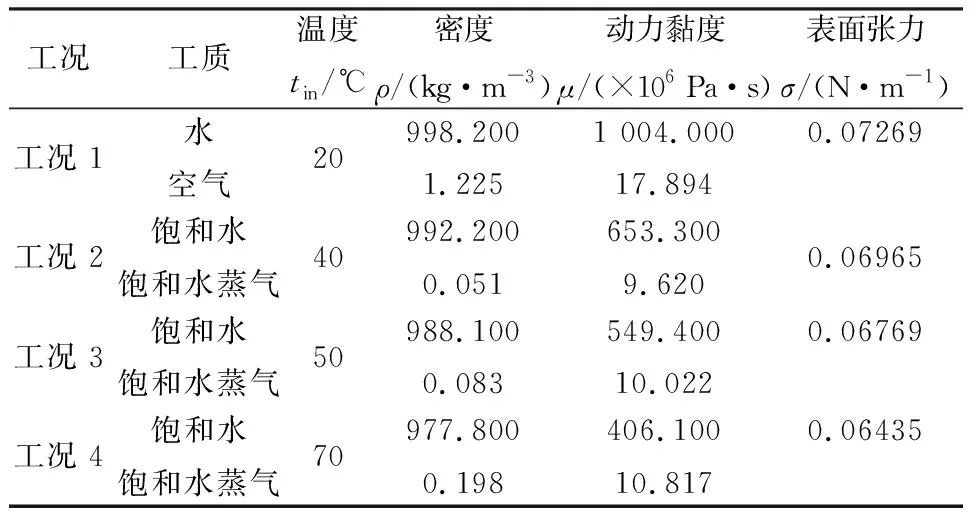
表1 流体工质物性参数

文中基于以下假设进行数值计算：

(1)水的喷淋密度范围0.12～0.3 kg/(m·s)，考虑水温对动力黏度的影响，液膜沿管外流动雷诺数Reo≤2 995，假设水在管外流动为层流[11]。

(2)忽略相变及传热。假设流动过程中工质物性保持不变，仅考虑不同工况对工质物性的影响。

(3)计算初始时，假设计算区域充满气相介质，压力为对应的饱和压力。

(4)假设液相体积分数为0.5处界面为气液相界面[12]。当管外流动稳定后，对周向角度θ=10°～170°的液膜厚度进行分析。

1.4 数值计算方法

1.4.1网格模型及边界条件

利用Gambit软件建立模型，采用结构化网格对计算区域进行划分，并对液膜区域网格做加密处理，单根水平管的网格划分见图4。

图4 单根水平管网格模型

在Gambit软件中对计算区域各边界条件进行如下设置。

(1)将A边界设置为速度进口边界条件，假设进口速度均匀分布，具体数值根据水的喷淋密度计算得到。

(2)B、C边界均设置为压力进口边界条件，进口的表压设为0。

(3)D边界设置为压力出口边界, 出口的表压设为0。

(4)E边界为换热管外壁面，设置为无滑移壁面边界条件。同时，将水与壁面的接触角设置为0°，以保证壁面完全润湿[13]。

(5)F、G边界设置为对称边界条件。

1.4.2求解器设置

文中模拟二维不可压缩常物性非定常流动过程，该过程流体力学控制方程[14]由连续性方程和动量方程组成。利用Fluent软件，选择2D瞬态求解器进行数值计算，求解器设置如下。

(1)采用VOF模型追踪气液相界面，并选用计算精度较高的Geo-Reconstruct算法。

(2)压力-速度耦合方式选用PISO算法。

(3)压力离散方式选用Body force weighted算法。

(4)选用CSF模型计算水的表面张力。

(5)考虑重力的影响，设置重力加速度为9.81 m/s2。

2 无关性验证及数值模拟方法验证

2.1 无关性验证

非定常流动数值计算过程中，时间步长的选取和网格划分对计算结果有很大的影响。当时间步长小于0.1 ms时计算结果满足时间步长无关性[7,8]，求解时设置时间步长在0.05～0.01 ms自动调整，同时将Courant number控制在1以内，以防计算结果失真。

当改变网格密度对计算结果的影响在5%以内时，可以认为计算结果满足网格无关性[15]，据此对不同管外径的计算模型均进行网格无关性验证。现选取水-空气两相流动作为研究对象，以管外径为19 mm、水的喷淋密度为0.3 kg/(m·s)为例，介绍网格无关性验证过程。利用边界层技术对管外液体区域网格进行局部加密，建立了网格数为8 552、12 026、17 359、23 775的4种计算模型，不同网格数时管外液膜厚度分布见图5。

图5 不同网格数时管外液膜厚度分布

由图5可知，网格数从17 359增大到23 775时，液膜厚度最大相对误差为2.62%，此计算结果满足网格无关性要求。

选择网格数为23 775的划分方法处理计算区域，即近壁面边界层按0.1 mm划分为20层(共计2 mm)，其余区域采用pave格式划分四边形面网格，单元尺寸为0.3 mm。

2.2 数值模拟方法验证

为验证所用数值模拟方法的正确性，对文献[4]中以水为介质、Reo=574、管间距S1=6.4 mm、S2=9.5 mm的圆管实验工况进行模拟，将液膜厚度模拟值同文献[4]中实验值作比较，见图6。

图6 液膜厚度实验值与模拟值比较

由图6可知，液膜厚度的模拟值与实验值沿管外周向角度分布规律基本一致，均呈现先减小后增大的趋势。液膜厚度模拟值在上半管周较实验值偏大，而在下半管周与实验值较为吻合。

为了对液膜厚度模拟值与实验值的误差进行定量分析，以液膜厚度实验值为基准与模拟值进行比较，得到误差散点图，见图7。

由图7可知，89%的液膜厚度模拟值与实验值的误差在±25%以内。产生误差的原因可能有三方面：一是文中采用简化的二维模型，忽略了轴向液膜的影响；二是模拟过程中作出的假设及边界条件的设定与实际情况具有一定的差异性；三是实验测量过程中存在不可避免的误差。

图7 基于液膜厚度实验值的模拟误差对比散点图

综上可知，利用文中模拟方法捕捉气液相界面并研究管外液膜厚度的分布规律是可行的。

3 液膜厚度数值模拟结果及分析

3.1 喷淋密度对液膜厚度的影响

改变水的喷淋密度，会对水在水平管管外流动及液膜厚度的分布产生影响。以管外径为19 mm建立计算模型，选择工况1进行模拟分析，得到不同喷淋密度下液膜厚度沿管外周向角度的分布情况，见图8。

图8 不同喷淋密度下液膜厚度沿管外周向角度的分布

由图8可知，①当喷淋密度一定时，θ=10°～90°内液膜厚度快速减小，随后减小趋势变缓，并在θ=120°～150°出现最小值，靠近管底部时液膜厚度有小幅度增大。②当喷淋密度增加时，液膜厚度在整个管周均明显增大。③下半管周(θ=90°～170°)液膜厚度分布相较于上半管周(θ=10°～90°)更均匀。这是因为下半管周液膜在重力、表面张力等作用下流动，而上半管周液膜流动过程中还受到冲击作用的显著影响，所以上半管周液膜流速变化快，液膜厚度也随之迅速减小。

3.2 换热管外径对液膜厚度的影响

不同的换热管外径直接改变液膜在管外流动的轨迹，进而影响液膜厚度沿管周的分布。对工况1进行模拟分析，水的喷淋密度为0.25 kg/(m·s)时管外径变化对液膜厚度的影响见图9。

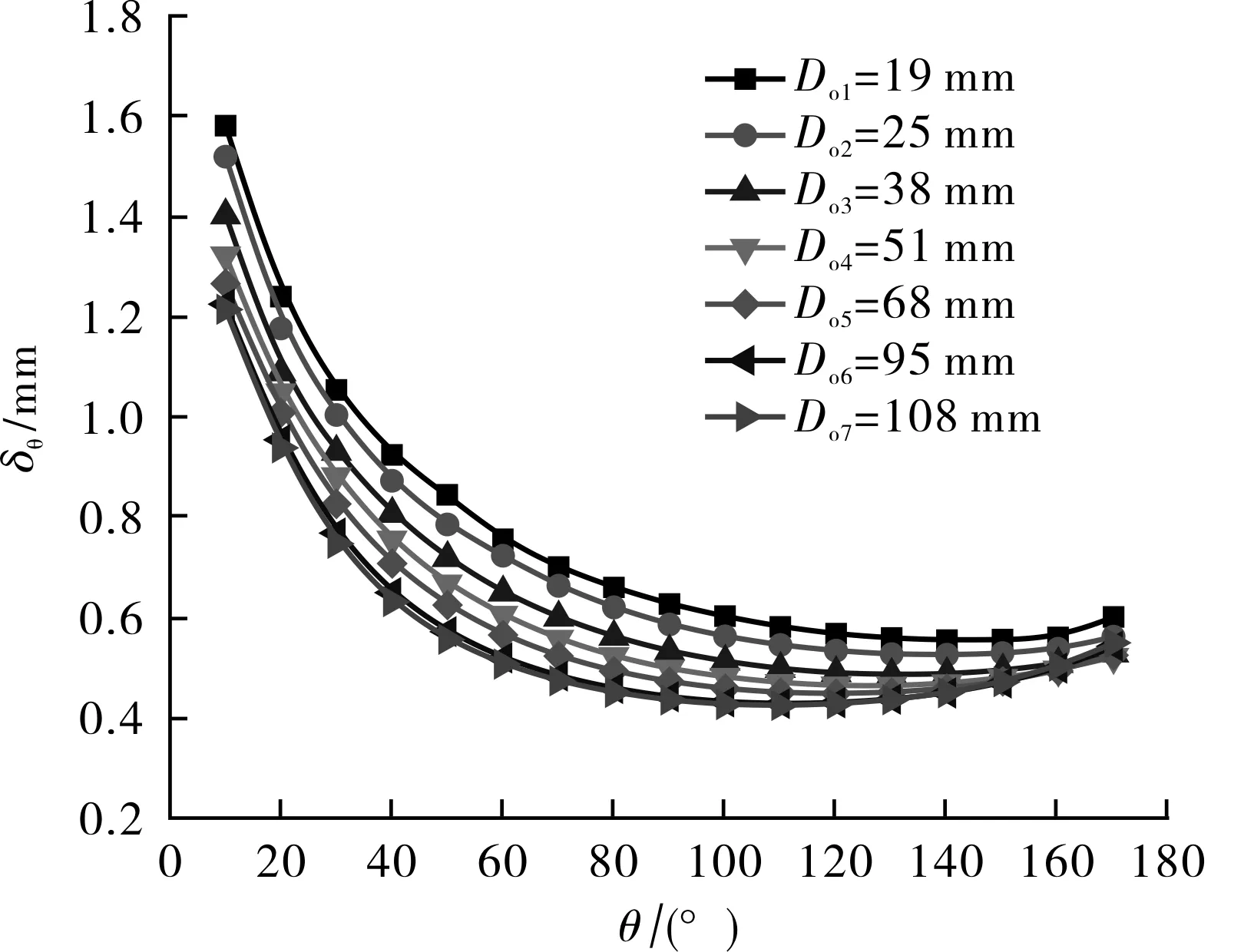
图9 相同喷淋密度和不同管外径条件下液膜厚度随周向角度的分布

由图9可知，①当喷淋密度一定时，不同管外径下液膜厚度随周向角度变化规律一致。②当管外径增大时，液膜厚度的分布范围变窄，液膜厚度分布越均匀。原因是管外径增大时，圆管曲率半径减小使液膜沿管外壁面流动的变化减缓。另外，液体接触管顶时产生冲击作用的影响区域也随管外径增大而减小，在这两方面作用的影响下液膜厚度分布变得更均匀。

对不同角度处液膜厚度取算术平均值，记为平均液膜厚度δm。不同喷淋密度下，平均液膜厚度δm随管外径的变化规律见图10。

图10 不同喷淋密度下平均液膜厚度随管外径的变化

由图10可知，相同喷淋密度下，平均液膜厚度随着管外径的增大而减小，但减小趋势逐渐变缓。分析认为，①当管外径增大时，液体自管顶流动到相同周向角度处经过的距离增加，重力对液体做功增加，使液膜流经同一周向角度处速度变大，所以液膜厚度减小。②当管外径Do在51～108 mm内增大时，圆管曲率半径减小幅度降低，液膜沿管外壁面流动时受到管外径改变的影响减小。因此，管外径较大时，液膜厚度随管外径增大而减小的趋势变缓。

3.3 水温对液膜厚度的影响

不同温度下，水的性质会随之发生变化。为研究水温对管外液膜厚度分布的影响，选择了管外径为19 mm建立计算模型，在水的喷淋密度为0.12 kg/(m·s)条件下，对工况2、3、4进行模拟分析，得到水温对液膜厚度影响(图11)、水温对液膜平均速度um的影响(图12)。

图11 相同喷淋密度和不同水温条件下液膜厚度沿管外周向角度的分布

图12 相同喷淋密度和不同水温条件下液膜平均流动速度沿管外周向角度的分布

由图11、图12可以知道，①水温不变，当周向角度θ≤90°时，液膜平均速度快速增大，并且液膜厚度迅速减小；当90°<θ≤150°时，液膜厚度及液膜平均速度变化都趋于平缓，且液膜厚度最小值出现在120°≤θ≤150°。由于水在150°<θ≤170°内汇聚，液膜流动速度降低导致液膜厚度增大。②喷淋密度不变，随着水温的升高，管外同一周向角度处液膜平均速度增大，液膜厚度减小。这是由于水的动力黏度随温度升高而显著减小，导致水在管外流动过程中所受黏滞阻力减弱，液膜流经管外相同角度时重力对其作用增强，从而导致液膜流速加快，液膜厚度变薄。

4 结论

(1)当喷淋密度一定时，液膜厚度在周向角度θ≤90°时快速减小，在90°≤θ≤170°时，分布比较均匀。液膜厚度最小值出现在120°≤θ≤150°。当喷淋密度增大时，液膜厚度增加。

(2)当管外径增大时，液膜厚度减小，并且液膜分布更加均匀。当管外径在Ø19～Ø51 mm增大时，平均液膜厚度明显减小。当管外径在Ø51～Ø108 mm继续增大时，液膜平均厚度减小的幅度趋于平缓。

(3)当水温升高时，水的动力黏度显著减小，液膜平均速度增大，且液膜厚度变小。