挖掘几何本质 破解向量难题

□浙江省宁波市李惠利中学 杨 栋

一、抛砖引玉

人教A版高中数学必修4有一道典型的例题：2.4A组第2题，笔者以此为载体作变式题的拓展研究。

例1：（必修4习题2.4第2题改编）如图1，在△ABC中，a=6，c=8，b=10．

图1

图2

方法4：建立图2所示的平面直角坐标系，则B（0，0），C（6，0），A（0，8

通过例1的四个方法可以归纳出平面向量数量积常见的运算方法：用定义、用投影、基向量、坐标法等。四种方法各有特点，投影法相对比较直观，能反映问题的几何意义，甚至直接观察得到答案，本题要注意向量投影的正负。

二、抽丝剥茧

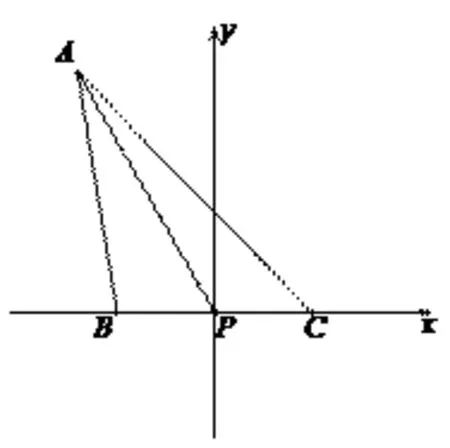
图3

P（0，0），B（-3，0），C（3，0），设A（x，y），则 由 ｜AP ｜==（-3-x，-y）·（3-x，-y）

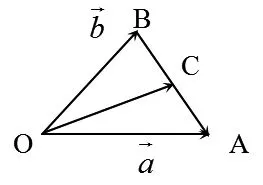
图4

在例1基础上加入动点P构造变式题：

变式2：已知△ABC中，AB=8，BC=6，AC=10，P点在平面ABC内，且，则 ｜PB ｜的取值范围为__________．

方法二：设O是AC的中点，建立图5所示的平面直角坐标系，则O（0，0），A（-5，0），C（5，0），设P（x，y），则由（-5-x，-y）·（5-x，-y）=x2-25+y2=-9，∴x2+y2=16，故点P的轨迹是以点O为圆心，4为半径的圆，∴ ｜PB ｜∈［｜BO ｜-4，｜BO ｜+4］，即 ｜PB ｜∈［1，9］．

图5

变化例1的部分已知条件，构造变式题：

同理可得

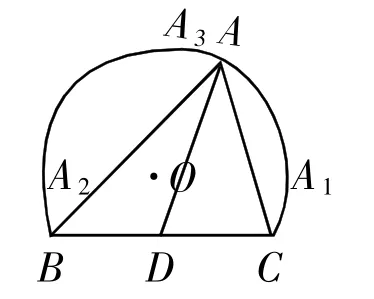
图6

利用向量投影的几何意义，结合极化恒等式，能快速突破此题。

结合动点P再构造变式题：

变式4：在△ABC中，AB=8，AC=10，P为BC的中点，求AP·BC的值。

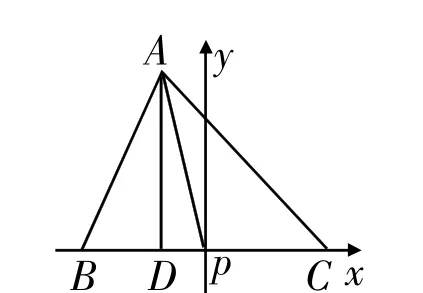
图7

方法三：过点A作AD⊥BC于D，设BD=m，CD=n，则

=AD2=102-n2，得n2-m2=36，∴AP·BC=18．

图8

解：方法一：如图8，过点P分别作PE⊥AB于点E，于PF⊥AC点F，

由点P为△ABC的外心知，点E，F分别为边AB，AC的中点，

方法二：过点P分别作PG⊥BC于点G，则点G为边BC的中点，且下同变式4可知

若点P改为边BC垂直平分线上的动点，同方法二过点P分别作PG⊥BC于点G，则点G为边BC的中点，且

几何本质：当点P在边BC垂直平分线上运动时，AP在BC=上的投影始终不变，所以数量积是定值．

把三角形△ABC和点P放在四边形中作变式研究：

变式5：如图9，在△ABC中，BC=6，BC边上的高为3，BCDE是△ABC的外接矩形，点P为CD上的动点，且满足的取值范围．

图9

解：方法一：建立图9所示的平面直角坐标系,设A（x，3），P（6，y），x∈［0，6］，y∈［0，3］y-3）=x2-6x-3y+9=+0（6，y）·（6-x，-3）=36-6x-3y=27-x2∈［-9，27］

方法二：由题意，AB⊥AP，CB⊥CP由数量积投影的几何意义得

坐标法可以转化为函数或不等式问题，而利用投影的几何意义，能更直观简洁地解决数量积问题．

把点P放在空间中作拓展研究：

变式6：如图10，△ABC是以∠A为顶角的等腰直角三角形，点D是底边BC的中点，点P是平面ABC外的一点，且满足的值。

图10

解：设E为AD的中点，由已知，AD垂直平分边BC，故DE·BC=0．

以上这些变式问题，都可以找到相应的几何背景，或挖掘其几何意义，从而获得事半功倍的效果．

三、直击高考

图11

结合几何直观能挖掘问题的几何背景，从而快速突破高考难题．此外，由的投影绝对值之和恒小于等于利用向量减法的三角形法则同理可此时夹角最大起点相同），

四、结束语

向量数量积作为向量的一种重要运算，反映和揭示了向量的代数特征和几何背景，凸显了向量作为数形结合经典载体的地位。向量的数量积问题可以从定义、基向量、坐标法、投影等角度入手，综合运用极化恒等式、三角函数、不等式、函数等有关知识突破。同时如果能多关注和挖掘数量积的几何意义，常常能另辟蹊径地收到事半功倍的效果，甚至还可以领略到命题者的出题意图和命题思路，加深对问题本质的理解，以达到举一反三、触类旁通的目的。