基于平均逻辑相似度的α-反向三I算法的鲁棒性

王 蓉，惠小静，井 美

延安大学 数学与计算机科学学院，陕西 延安 716000

1 引言

模糊控制的理论基础是模糊推理，1973年，Zadeh提出了模糊推理的CRI[1]算法，但是CRI算法不具有还原性且缺乏严格的逻辑基础。因此，我国学者王国俊教授等提出了模糊推理的三I[2]算法，该算法有良好的逻辑基础。因此诸多学者对此进行了研究，文献[3]提出反向三I支持算法和反向三I约束算法理论；文献[4]研究了基于反向支持度的三I算法；文献[5]研究了基于反向三I约束算法等。

设L是模糊推理系统，A是L中的模糊输入，B是L中的模糊输出。如果模糊输入A的微小偏差不会对模糊输出B产生很大的影响，则称模糊推理系统L具有良好的鲁棒性。鲁棒性问题与控制系统的相对稳定性有着密切的联系，因此许多学者对此进行了研究。文献[6]介绍了模糊集扰动的概念；文献[7]研究了CRI算法的鲁棒性；文献[8]研究了三I算法的鲁棒性。文献[9]用灵敏度的方法讨论了模糊推理的鲁棒性；文献[10]基于Minkowski距离研究了模糊推理的鲁棒性；文献[11]基于Moore距离研究了区间值模糊推理三I算法的鲁棒性。

用什么去衡量两个模糊集之间的偏差，文献[12]提出一种新的衡量模糊集之间远近程度的扰动参数，即极小逻辑相似度，极小逻辑相似度最终是用取小算子去对原始数据进行聚合，这样容易导致信息丢失。因此文献[13]是在极小相似度的基础上提出了一种新的扰动参数：平均逻辑相似度，采用平均逻辑相似度对原始数据做了更精细的处理，比极小相似度保留更多信息，其所得到的结果越精确。因此，在上述工作的基础上以平均逻辑相似度为扰动参数分别讨论了α-反向三I支持算法和α-反向三I约束算法的鲁棒性。

2 预备知识

X、Y为非空论域，F(X)、F(Y)分别是论域X与

定义2.3[14]T是格L上的t-模，若存在另一个二元算子ℜ:L2→L使得：T(a,b)≤c，当且仅当a≤ℜ(b,c),a,b,c∈L，则称(T,ℜ)为L上的伴随对，并且称(L,T,ℜ)为剩余格。

定义2.4[14]设T是格L上的左连续的t-模，则存在另一个二元算子ℜ：L2→L使得(T,ℜ)为L上的伴随对，其中

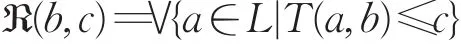
以下，称ℜ是由T诱导的剩余蕴涵。

定义2.5[15]设→：[0,1]2→[0,1]是[0,1]上的二元算子，若满足如下条件：

（1）0→0=1,0→1=1,1→1=1，1→0=0。

（2）关于第一变量不增，第二变量不减。则称→是[0,1]上的模糊蕴涵算子。

定义2.6[14]设→是[0,1]上的二元算子，若对任意的a,b,c,d∈[0,1],→满足如下条件：

（1）a→b=1当且仅当a≤b。

（2）a≤b→c当且仅当b≤a→c。

（3）a→(b→c)=b→(a→c)。

（4）1→a=a。论域Y上的模糊集的全体。

定义2.1[14]设L为完备格，二元算子T：L2→L被称为L上的一个t模，如果T满足交换律、结合律，对每个变量都不减，且∀x∈L,T(1,x)=x。

定义2.2[14]设T是格L上的t-模，T称为左连续的，如果对L的任意非空子集B，以下等式成立：

（6）a→b关于a单调不增，且关于b单调不减，那么→称为[0,1]上的正则蕴涵算子。

定义2.7[16]设(L,T,ℜ)是剩余格，∀a,b∈L，规定

a↔b=ℜ(a,b)∧ℜ(b,a),a,b∈L以下记为s(a,b)=a↔b。

定义2.8[17]设 X={x1,x2,…,xn},A,B∈F(X),→ 是[0，1]上满足的模糊蕴涵，令

称S∗(A,B)为A与B的平均逻辑相似度。

3 逻辑连接词的鲁棒性

引理 3.1[17]设 |X|=n,A,A′,B,B′∈F(X),x∈X,→是[0，1]上满足a+(a→b)≤1+b的正则蕴涵，T是L上左连续t-模，ℜ是T生成的剩余蕴涵，则有以下的不等式：

（1）s(A(x)∨ B(x),A′(x)∨ B′(x))≥s(A(x),A′(x))+s(B(x),B′(x))-1。

（2）s(A(x)∧ B(x),A′(x)∧ B′(x))≥s(A(x),A′(x))+s(B(x),B′(x))-1。

（3）s(T(A(x),B(x)),T(A′(x),B′(x)))≥s(A(x),A′(x))+s(B(x),B′(x))-1。

（4）s(ℜ(A(x),B(x)),ℜ(A′(x),B′(x)))≥s(A(x),A′(x))+s(B(x),B′(x))-1。

命题3.1[17]设|X|=n,A,A′,B,B′∈F(X),x∈X,→是[0，1]上满足a+(a→b)≤1+b的正则蕴涵，T是L上左连续 t-模，ℜ 是 T 生成的剩余蕴涵，若 S∗(A,A′)≥δ1，S∗(B,B′)≥δ2则

S∗(A∘B,A′∘B′)≥δ1+δ2-1,其中∘∈{∧,∨,ℜ,T}

命题3.2[17]设 |X|=n,A,A′,B,B′,C,C′∈F(X),x∈X,→是[0，1]上满足a+(a→b)≤1+b的正则蕴涵，T是L上左连续t-模，ℜ是T生成的剩余蕴涵，若S∗(A,A′)≥δ1，S∗(B,B′)≥δ2，S∗(C,C′)≥δ3，则

S∗(T(C,ℜ(A,B)),T(C′,ℜ(A′,B′)))≥δ1+δ2+δ3-2

4 α反向三I算法的鲁棒性

本章以平均逻辑相似度作为扰动参数分别讨论了α-反向三I支持算法和α-反向三I约束算法的鲁棒性。

引理4.1[17]令 ai,bi∈[0,1]，i=1,2,…,n,→ 是满足a+(a→b)≤1+b的正则蕴涵。则有：

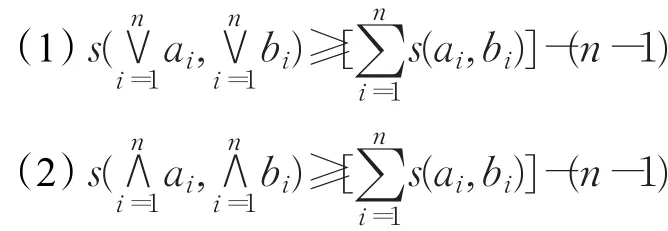
定理4.1[18]设([0,1],T,ℜ)是剩余格，α∈[0,1]。A,A∗∈F(X)，B,B∗∈ F(Y),则：

（1）FMP(A,B,A∗)的 α-反向三I支持算法解 B∗的形式如下：

（2）FMT(A,B,B∗)的 α-反向三I支持算法解 A∗的形式如下：

定理4.2 设→是[0，1]上满足a+(a→b)≤1+b的正则蕴涵，T是L上左连续t-模，ℜ是T生成的剩余蕴 涵 。 令 |X|=n,|Y|=m,A,A′,A∗,A∗′∈F(X),B,B′,B∗,B∗′∈F(Y)且 B∗和 B∗′分别是定理4.1FMP(A,B,A∗)和FMP(A′,B′,A∗′)的 α-反向三I支持算法的解。

若 S∗(A,A′)≥δ1，S∗(B,B′)≥δ2，S∗(A∗,A∗′)≥δ3，则S∗(B∗,B∗′)≥1-n(3-δ1-δ2-δ3)。

证明 S∗(B∗,B∗′)=

定理4.3 设→是[0，1]上满足a+(a→b)≤1+b的正则蕴涵，T是L上左连续t-模，ℜ是T生成的剩余蕴 涵 。 令 |X|=n,|Y|=m,A,A′,A∗,A∗′∈F(X),B,B′,B∗,B∗′∈F(Y)且 A∗和 A∗′分别是定理 4.1FMT(A,B,B∗)和 FMT(A′,B′,B∗′)的 α-反向三I支持算法的解。

若 S∗(A,A′)≥δ1，S∗(B,B′)≥δ2，S∗(B∗,B∗′)≥δ3则S∗(A∗,A∗′)≥1-m(3-δ1-δ2-δ3)。

证明 S∗(A∗,A∗′)=

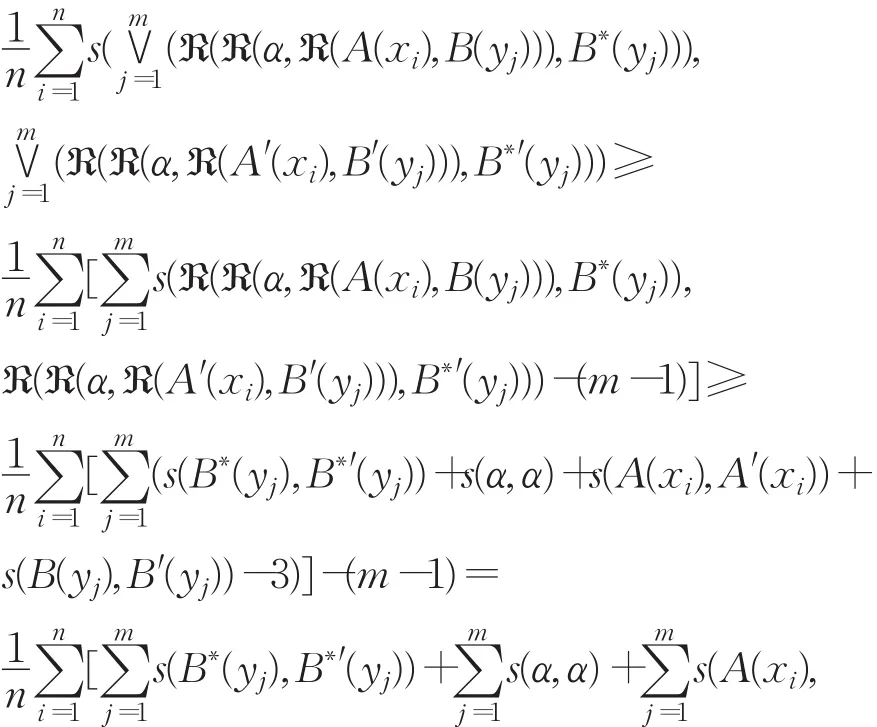
注 由定理4.2和定理4.3可知当假设δi(i=1,2,3)无限接近1，可得 S∗(B∗,B∗′)也非常接近1。由以上事实可见，当输入A,B和A∗存在微小偏差将会导致FMP(A,B,A∗)的α-反向三I支持算法的解B∗微小的改变。因此关于FMP问题的α-反向三I支持算法有良好的鲁棒性。同理分析可知FMT问题的α-反向三I支持算法也具有良好的鲁棒性。

定理4.4[19]设([0,1],T,ℜ)是剩余格，α∈[0,1]A,A∗∈F(X)，B,B∗∈ F(Y),则

（1）FMP(A,B,A∗)的 α-反向三I约束算法解 B∗的形式如下：

（2）FMT(A,B,B∗)的 α-反向三I约束算法解 A∗的形式如下：

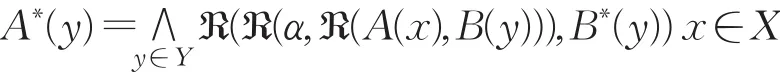
定理4.5 设→是[0，1]上满足a+(a→b)≤1+b的正则蕴涵，T是L上左连续t-模，ℜ是T生成的剩余蕴 涵 。 令 |X|=n,|Y|=m,A,A′,A∗,A∗′∈F(X),B,B′,B∗,B∗′∈F(Y)，且 B∗和 B∗′分别是定理4.4FMP(A,B,A∗)和 FMP(A′,B′,A∗′)的 α-反向三I约束算法的解。

若 S∗(A,A′)≥δ1，S∗(B,B′)≥δ2，S∗(A∗,A∗′)≥δ3，则S∗(B∗,B∗′)≥1-n(3-δ1-δ2-δ3)。

证明 S∗(B∗,B∗′)=

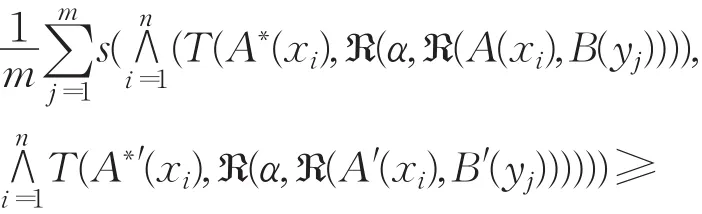
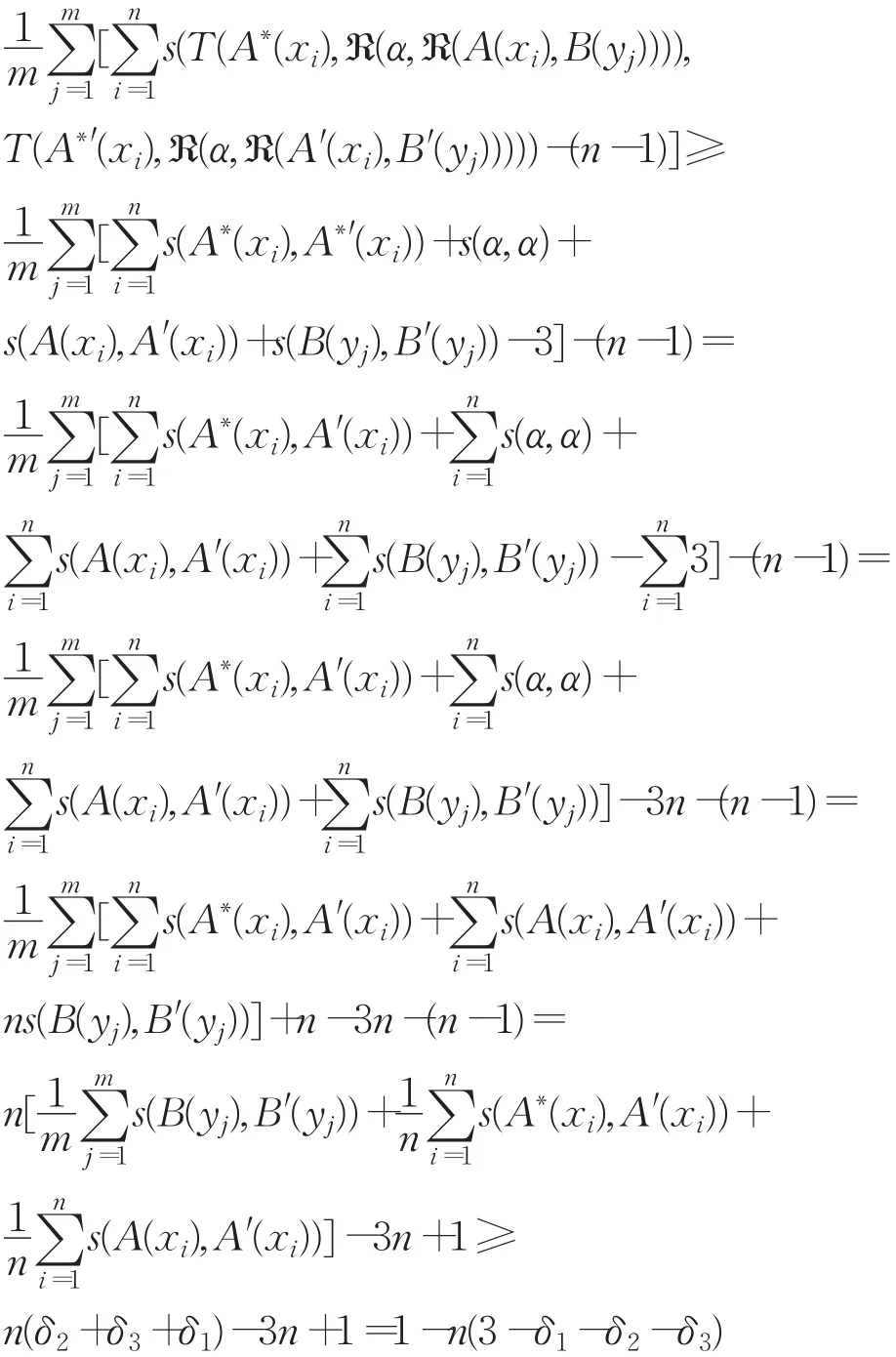
定理4.6 设→是[0，1]上满足a+(a→b)≤1+b的正则蕴涵，T是L上左连续t-模，ℜ是T生成的剩余蕴 涵 。 令 |X|=n,|Y|=m,A,A′,A∗,A∗′∈F(X),B,B′,B∗,B∗′∈F(Y)且 A∗和 A∗′分别是定理 4.4FMT(A,B,B∗)和 FMT(A′,B′,B∗′)的 α-反向三I约束算法的解。

若 S∗(A,A′)≥δ1，S∗(B,B′)≥δ2，S∗(B∗,B∗′)≥δ3，则S∗(A∗,A∗′)≥1-m(3-δ1-δ2-δ3)。

证明 S∗(A∗,A∗′)=

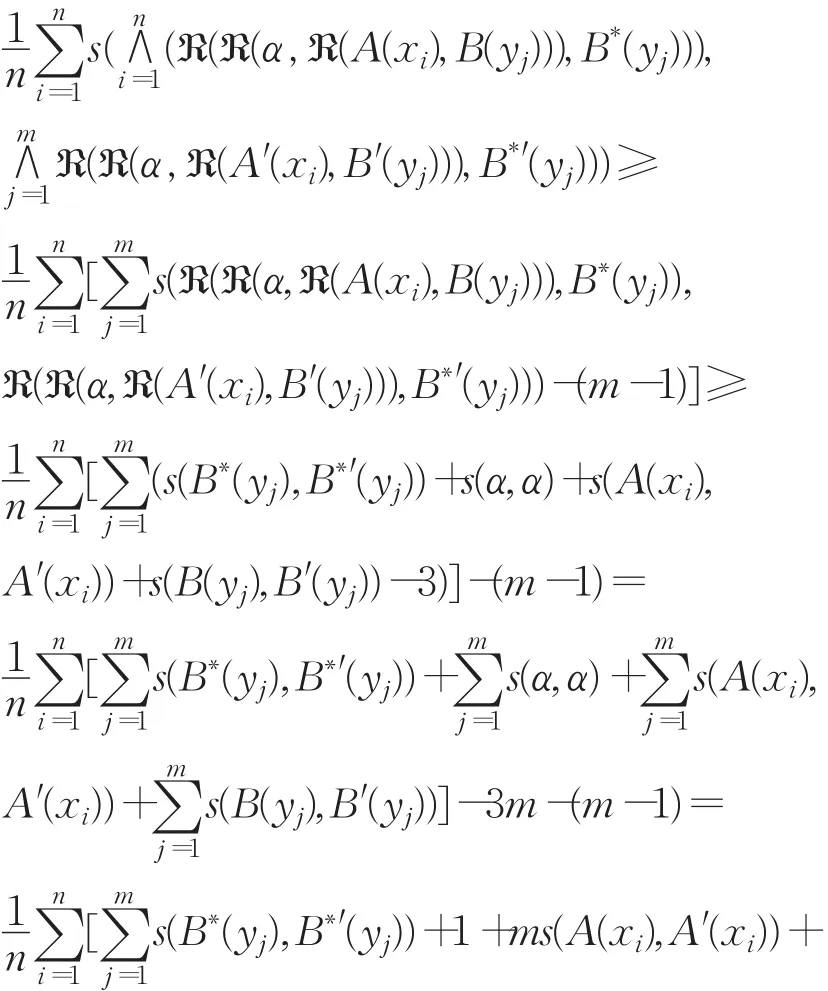
注 由定理4.5和定理4.6可知当假设δi(i=1,2,3)无限接近1，可得 S∗(B∗,B∗′)也非常接近1。由以上事实可见，当输入 A,B和 A∗存在微小偏差将会导致FMP(A,B,A∗)的 α-反向三I约束算法解 B∗微小的改变。因此关于FMP问题的α-反向三I约束算法有良好的鲁棒性。同理分析可知FMT问题的α-反向三I约束算法也具有良好的鲁棒性。

5 结束语

本文以平均逻辑相似度作为衡量扰动的指标，分别研究了α-反向三I支持算法和α-反向三I约束算法的鲁棒性。把模糊集拓展到区间值模糊集，讨论基于区间值模糊推理α-反向三I支持算法和基于区间值模糊推理α-反向三I约束算法的鲁棒性，将于另文中讨论。