报废汽车挡风玻璃边缘轮廓的双圆弧优化拟合方法研究

毛慧俊 ，周自强 ，蒋波

（1.苏州大学机电工程学院，江苏苏州215000；2.常熟理工学院机械工程学院，江苏常熟215500；3.江苏省机电产品循环利用技术重点建设实验室，江苏常熟215500）

随着我国汽车保有量的持续增加，目前中国已经成为世界上汽车保有量最大的国家。但同时报废汽车的回收与处理也成为日益严重的社会问题[1]。过去由于对拆解回收行业的技术支持不足，整个报废汽车拆解行业大多处于简单的分解和材料回收的层面。实际上报废汽车上仍然有大量的零部件是可以再利用或者再制造的，通过这种方式不仅可以增加报废汽车拆解企业的整体经济效益，也有利于降低全社会对自然资源的消耗[2]。挡风玻璃由于是非金属材料，且不属于运动部件，基本可以不考虑疲劳寿命。因此在无损拆解后是可以在维修市场上继续利用的。而目前影响挡风玻璃再利用的主要原因是拆卸成本较高，如果能够通过自动化设备快速高效地拆卸档风玻璃，就能够大大提高挡风玻璃的再利用率。

在用机器视觉对挡风玻璃的边缘数据进行提取后，由于图像中环境噪声的影响，会使得很多边缘点偏离理论轮廓。如何通过技术手段对这些存在误差的轮廓特征点进行光顺处理，并生成运动控制系统能够接受的指令，是整个挡风玻璃自动切割机的重要环节。

1 基于机器视觉的报废汽车挡风玻璃轮廓点提取

对报废汽车挡风玻璃的轮廓特征提取方法如图1所示，首先通过摄像头采集挡风玻璃的平面图像。然后通过边缘锐化、最大轮廓提取、二值化等图像处理算法，最后得到挡风玻璃边缘轮廓的连续离散点。对这些离散点可以通过曲率的变化关系提取其轮廓特征点，然后将这些轮廓特征点拟合成曲线轨迹，挡风玻璃自动切割机的跟踪传感器在控制系统的作用下，沿该曲线轨迹运行一周，通过所获得的纵向偏差数据和原有的曲线轨迹形成挡风玻璃的三维切割轨迹，并最终控制切割头将挡风玻璃的边缘车身进行切割分离。

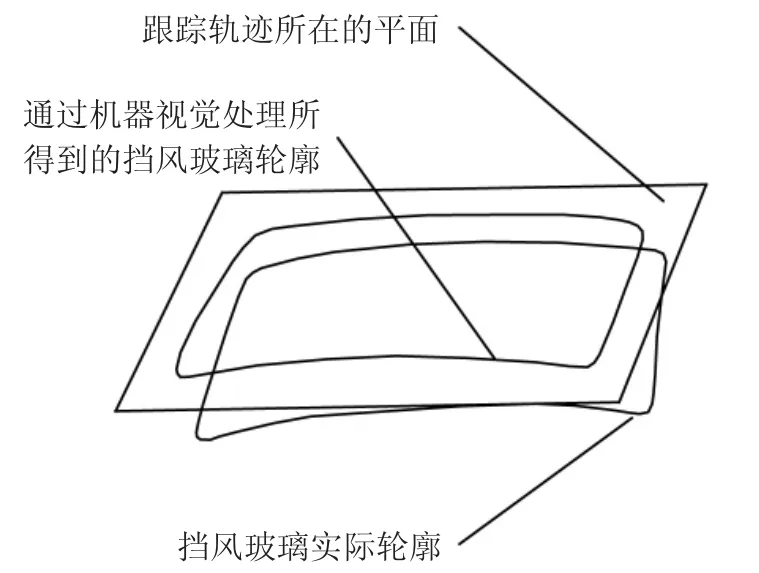
图1 挡风玻璃轮廓特征提取方法

2 基于最小二乘法的轮廓特征点曲线拟合

由于图像噪声的影响，这些轮廓特征点会存在一定的误差，因此如果用小直线段直接拟合这些特征点，就会造成很大的轨迹误差。其次，全部用直线段表示的曲线轨迹对于设备的平稳运行也是不利的。因此需要通过理论方法来消除这些误差数据。最小二乘法是一种优化拟合算法，该方法并不要求拟合曲线通过所有的特征点，大偏差特征点的作用会通过残差计算而被抑制，因此可以从总体上提高拟合曲线的精度。

最小二乘法拟合的基本原理是构造一条曲线，使原数据点与拟合点的误差的平方和为最小，那么这条曲线就是最小二乘拟合曲线，该曲线的函数表达式为最小二乘拟合函数[3]。

在Matlab中，polyfit函数可以有效地处理最小二乘曲线拟合问题。如图2所示，polyfit函数的基本原理是构造一个多项式函数f（x）=a1xn+a2xn-1+···+anx+b，使其满足最小二乘原理，并返回多项式的系数矩阵。

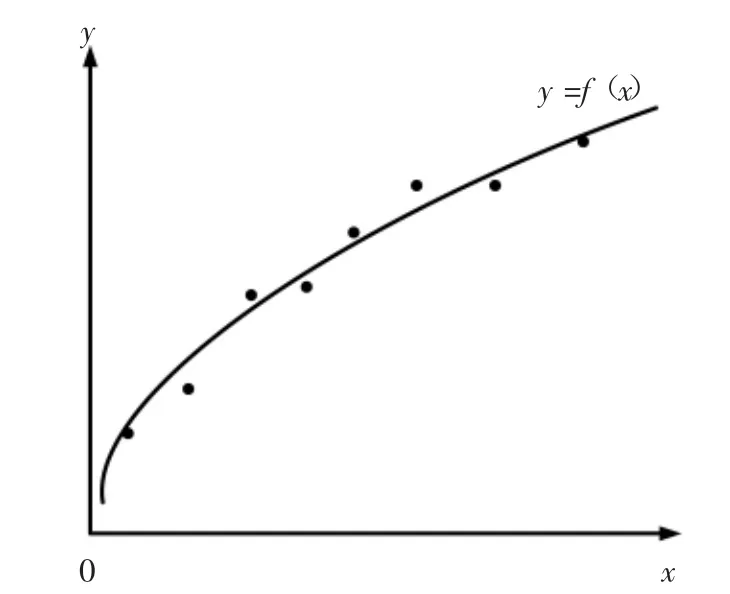
图2 最小二乘拟合原理图

3 基于双圆弧的轮廓轨迹表征

由于通过最小二乘法得到的拟合曲线的方程是一个多项式方程，该方程无法直接对挡风玻璃自动切割机的运动控制系统进行控制，必须将其转换成运动控制系统能够接受的指令信号。虽然目前很多运动控制系统可以接受插补方式的运动控制，但是该方法计算量大，系统的运行速度受到很大限制。而一般的经济性运动控制系统只支持直线插补和圆弧插补指令，因此需要在指令数和指令精度之间进行综合优化。

双圆弧拟合方法的基本原理是在每两个相邻的节点之间插入两段彼此相切圆弧，同时过每一个节点的左右两段圆弧也依次相切，从而形成整体的G1连续光滑的曲线[4]。为了确定唯一的双圆弧拟合曲线，需要确定节点位置及公切点位置。目前，大多数研究集中在公切点的选取上，主要有以下3种方式：内心法，即公切点的位置选在由相邻节点及节点矢量所构成的三角形的内心；平行弦法，即取两节点连线的斜率作为公切点的斜率；优化双圆弧拟合方法，它是通过改变公切点的斜率来控制误差大小，使每段双圆弧均在给定的误差范围内。

3.1 优化双圆弧拟合模型

采用优化双圆弧拟合方法，通过合理的选择公切点的斜率，就可以将拟合误差控制在给定范围内，从而提高轮廓提取时的精度。如图3所示，为了对双圆弧拟合模型进行研究，设曲线上相邻的两节点为Pi，Pi+1，它们的切矢方向分别为PiP，PPi+1，这两条切线交于P，它们的斜率分别为Ti和Ti+1，N为双圆弧拟合的公切点，过N作双圆弧的切线交PPi和PPi+1于点P3，P4，设a=PiP，b=PPi+1，c=PiPi+1，过点 Pi作 P3P4的平行线交 PPi+1于点P5，此时，若公切点N的斜率TN已知，则PiP5和Pi+1P5的长度均可求出。

由圆的切线长定理可得：PiP3=P3N，Pi+1P4=P4N，因此，要想求公切点N的坐标，首先要求点P3的坐标。设m=PiP3，d=PiP5，e=Pi+1P5，由文献［5］可知：

当P3的坐标确定后，即可由等式PiP3=P3N和TN的值进一步确定公切点N的坐标。现对式（1）作进一步讨论。

（1）当 d＞e时，m＞0，此时公切点 N 唯一确定；若此时 Ti＜TN＜Tp，则 m 可由式（1）确定；当 Tp＜TN＜Ti+1时，此时，点P5落在线段PPi+1的延长线上，根据△PP3P4和△PPiPi+1相似，可得出：

（2）当 d＜e时，则 m＜0，此时应以点 Pi+1为基点，过Pi+1作P3P4的平行线，同理亦可求出公切点N的坐标。

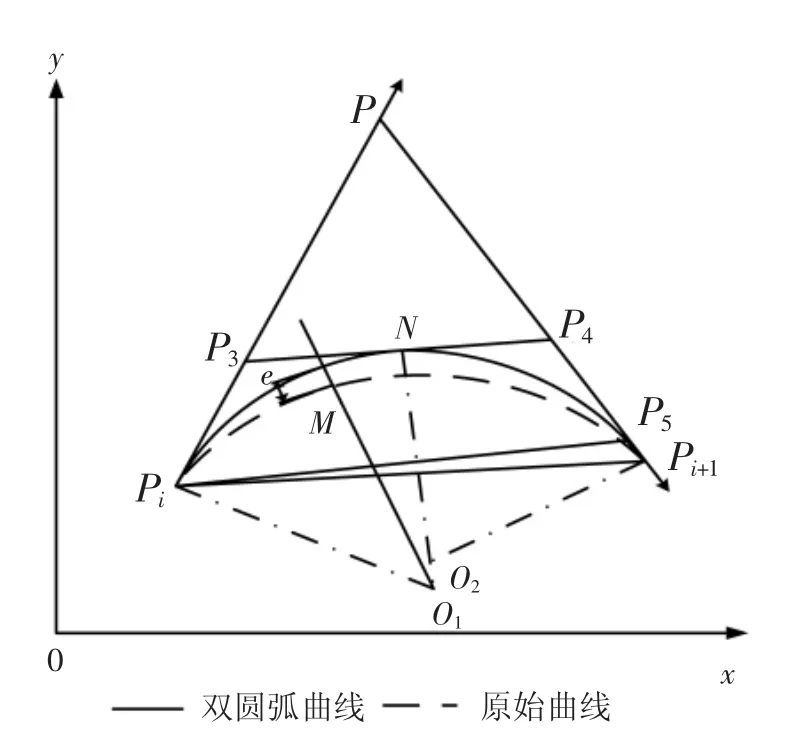
图3 双圆弧拟合基本原理图

3.2 公切点斜率TN的选取方法

采用优化双圆弧拟合模型，最重要的就是公切点斜率TN的选取方法。选择恰当的TN值，可以有效地减小误差。在以往的研究中，多是采用随机取值的方法，满足误差要求则TN值符合要求，不满足则重新取值。

文中在TN的取值方法上作了一定改进，由于目标曲线的曲率变化较小，因此，可采用均分法取TN值，即将Ti～Ti+1均分为4～5段，计算出在每个TN取值下的最大拟合误差，比较过后选取其中的最小值及其对应的斜率TN，采用这种方法得到的误差相对较小，但该方法仅适用于曲率变化不大的曲线，而对于曲率变化大的曲线，分段数会变多，大大增加计算量，延长求解时间。

3.3 双圆弧拟合的误差分析

双圆弧拟合曲线的误差通常是用法向误差来表示的，如图3所示，当数据点在以O1为圆心的圆弧一侧时，其误差如式（3）所示：

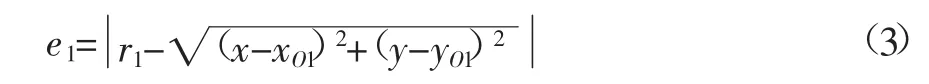
相反，若数据点在以O2为圆心的圆弧一侧时，误差表达式为：

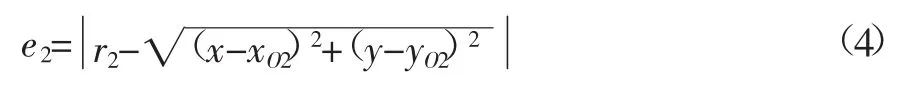
为了求出最大误差值，可对式（3）中根号内部分进行求导[6]：

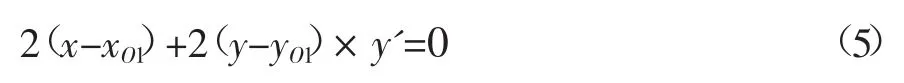
整理得：

式中：x，y 为数据点的坐标；xO1，yO1为圆心 O1的坐标；y'为y的导数。

由式（6）可以看出，当原始曲线上的点的法向量穿过所在圆弧的圆心位置时，该处产生的误差为最大值，只要该点满足误差要求，则该段双圆弧曲线均能达到规定的误差要求。

4 计算实例

为验证优化双圆弧拟合及TN取值方法在轮廓提取时的正确性，使用Matlab软件编写程序，绘制经过最小二乘拟合和双圆弧拟合后整块平面玻璃的轮廓曲线。图4a为采集的汽车挡风玻璃的平面图像，在经过边缘锐化、最大轮廓提取、二值化等图像处理后，获得其部分轮廓点的坐标，如图4b所示。

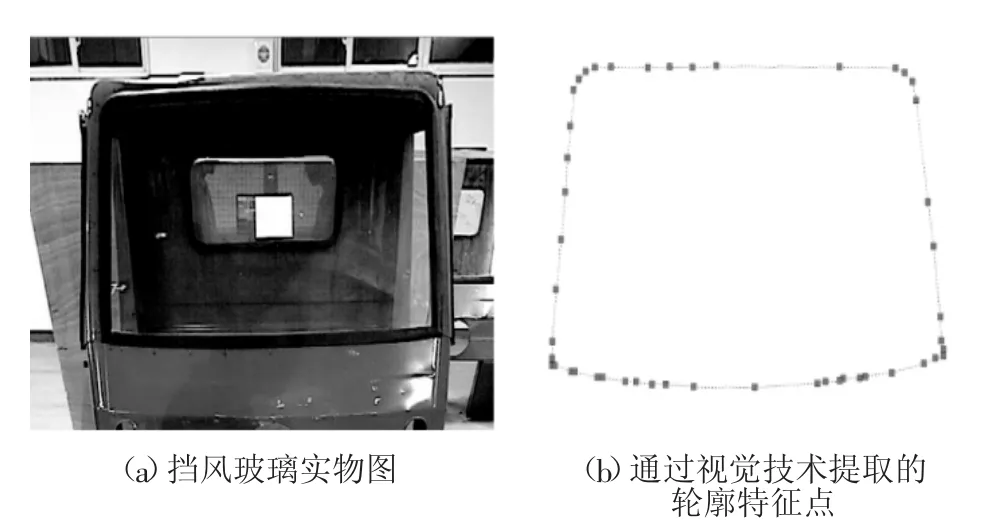
图4

获得轮廓数据点的坐标后，使用Matlab软件编程，求出双圆弧拟合的节点坐标、公切点N的坐标及圆心O1，O2的坐标，并使用plot函数绘制整个经过双圆弧拟合后的挡风玻璃轮廓曲线，程序运行结果如图5所示。

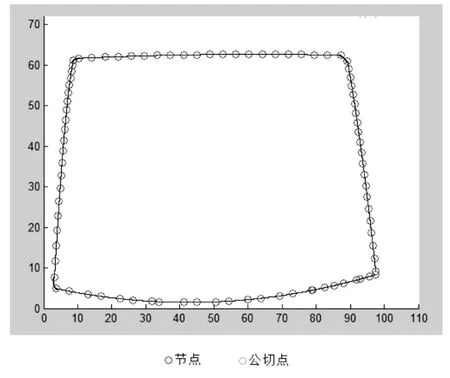
图5 挡风玻璃轮廓拟合程序运行图

5 结论

提出一种将最小二乘法与双圆弧拟合方法相结合的挡风玻璃轮廓点拟合方法。首先通过图像处理技术提取挡风玻璃部分轮廓点的坐标，然后使用最小二乘拟合法对轮廓点进行曲线拟合，最后采用优化双圆弧拟合方法对整个轮廓曲线进行优化拟合处理，以便控制挡风玻璃自动切割机的运动控制系统，进而规划其切割路径。采用该方法明显消除了基于图像处理所得到的轮廓点中误差较大的特征点，形成了较为光滑的拟合曲线，从而有利于后续的运动控制的实现。