基于特征融合的静态手势识别∗

缑新科 王 瑶

（兰州理工大学电气工程与信息工程学院 兰州 730050）

1 引言

人机交互就是人与计算机为协同完成某项任务而进行的信息交换过程。随着科学技术的发展，人机交互技术的研究也日益受到众多学者重视，成为研究的热点。针对传统人机交互的缺点与不足，最近几年发展了较多新的交互模式，如指纹识别、人脸识别、语音识别、手势识别、运动跟踪等等，手势识别交互作为一种自然、人性化的交互方式被越来越多的采用。手势识别可分为静态手势识别和动态手势识别，本文主要研究静态手势识别。

现有的识别方法，其中大多数是基于机器学习的检测方法。该检测方法主要包括两个重要方面，一个是特征提取，另一个是学习算法。图像特征提取主要：Haar-like［1］、HOG（Histogram of Oriented Gradient）［2］和 LBP（Local Binary Pattern，局部二值模式）［3］等。学习算法主要有支持向量机（SVM）和级联Adaboost。SVM通过核函数将样本映射到能够进行线性可分的高维空间，在高维空间进行点积运算即可得到判别结果，鲁棒性较好，解决小样本情况下的机器学习问题。Adahoost是一种迭代算法，针对同一训练集反复训练并且根据上一次样本的权重得到不同弱分类器的组合形成最终的强分类器，实时性好。本文针对单一特征的局限性和融合特征维度过高的缺点，提出了利用PCA降维HOG特征［4］再与LBP特征融合［5～6］的描述算子选用SVM分类器进行手势识别。

2 理论基础

2.1 HOG特征

像素的边缘分布的方向可以较好的描述一副图像中对象的局部外观或者外形，以此为理论基础Dalal和Triggs在2005年提出了HOG特征的描述算子［7］，提取HOG特征的具体为以下步骤［8］：

1）标准化的Gamma空间和颜色空间。平方根Gamma标准化可以调节图像的对比度，降低光照变化所造成的影响，同时可以抑制噪音的干扰。Gamma=1/2时压缩公式：

2）计算图像每个像素的梯度（包括大小和方向），主要是为了捕获轮廓信息，同时进一步弱化光照的干扰。

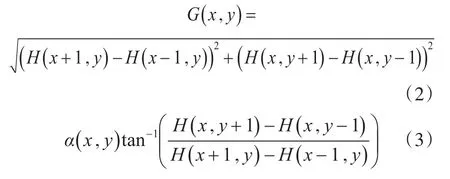
其中，G(x ，y )，α(x ，y )，H(x ，y)分别表示像素点的梯度幅值、梯度方向以及像素点的灰度值。

3）实验中的检测窗口大小是64*64，块大小是16*16，块的步进是8*8，每个块划分为大小为8*8的胞元。设置每个胞元的直方图的bin值为9，所以每个块有4个胞元，也就是每个块有4*9=36个特征向量。利用公式（window_size-block_size）/block_stride+1可得每个窗口有49个块，所以一个64*64的检测窗口的HOG特征向量为49*36=1764维。如图1所示是提取HOG的特征图。

图1 提取的HOG特征

2.2 LBP特征

LBP是一种用来描述图像局部纹理特征的算子；它具有旋转不变性和灰度不变性等显著的优点。它是首先由T.Ojala，M.Pietikäinen和D.Har⁃wood在1994年提出，用于纹理特征提取［9］。目标的纹理特征非常稳定，不受背景颜色和光照的影响，所以使用纹理特征有助于图像之间的区分。

基本的LBP算子是对于图像中的每一个像素点，以该点的灰度值作为阈值，对其3*3邻域内的像素灰度值作比较，若周围8个像素点的值大于阈值，则为1，否则为0。按照一定的顺序比较，得到一个8位的二进制数，以此二进制数作为对该像素点的响应。图2所示为提取过程。

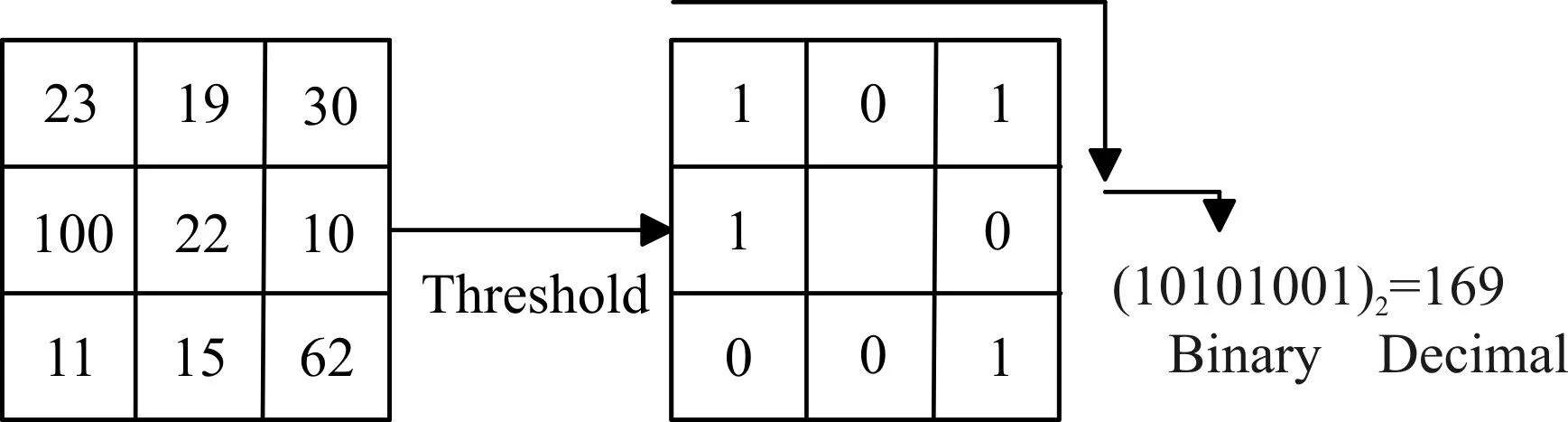
图2 基本LBP算子

其计算公式如下：

后来，对基本LBP算子进行了改进。采用圆形的邻域并结合双线性插值运算，从而可以获得任意半径和任意数目的邻域像素点。但是这样的LBP描述特征能力有限，且不具备旋转不变性。很容易想象，如果图片进行了旋转，则LBP值也会随之改变。

本文采用了LBP旋转不变模式与等价模式相结合的模式。旋转LBP模式一幅图像中存在分布出现的频率差异较大的缺陷，得到的效果并不是很好，而研究者发现，在实际图像中，90%以上LBP模式最多只包含两次从1～0或从0～1的跳变。对于8个采样点，灰度不变性LBP将产生256种输出，旋转不变性LBP将产生36种输出，等价模式中有58种输出，而基于等价的旋转不变LBP将只有9种输出（如图2所示）［10］。将检测窗口划分为16*16的小区域（cell），则共有16个cell，每个cell有9种输出，所以LBP特征向量为9*4*4=144维。旋转不变的等价LBP的计算公式如下：

图3是分别原图（a）、旋转不变LBP图（b）、等价LBP图（c）和旋转不变的等价LBP图（d）。由图3分析可知，随着输出种类的不断减少，得到的LBP图也就越来越黑。

图3 四种LBP图

2.3 特征提取与融合

HOG-PCA特征提取：

HOG特征向量维度很高，所以存在大量的冗余信息而导致检测速度慢等不足。所以对HOG特征向量进行降维处理就显得尤为重要，本文运用PCA（主成分分析法）对特征降维［11］。PCA的实质就是在能尽可能好地代表原特征的情况下，将原特征进行线性变换、映射到低纬度且相互正交的空间上。

PCA就是通过将原来的变量做线性投影形成新的变量。通过式（5）计算特征的主成分得到式（6）

其中 y表示主成分特征，xˉ为训练样本的特征均值，xi为提取的原特征向量，UT为协方差矩阵，UT的计算公式如式（7）所示：

PCA降维HOG特征步骤如下：

1）对所有训练样本中对应像素点的HOG特征的进行零均值化，即减去这一行的均值。由前面可知xˉ是一个1764维的特性向量。

2）通过训练样本的HOG特征，样本均值，根据式（7）可以计算协方差矩阵及协方差矩阵的特征值及对应的特征向量。其中，协方差矩阵的大小为1764*1764。

3）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵，对训练样本中的每个HOG特征向量，通过式（6）进行降维，得到降维后的特征，向量维数为k维，即HOG-PCA特征。

2.4 LBP特征与HOG-PCA特征融合

当背景覆盖凌乱的噪声边缘时，HOG处理效果很差，而LBP却可以处理，它可以过滤出噪声，结合了边缘/局部形状信息还有纹理信息，能够很好的表示手势的特征，所以将HOG特征和LBP特征联合起来［12～13］，既可以获取手势的梯度信息，又可以获取手势的纹理信息，提高在复杂背景的手势的识别率。目前常用的特征融合方法为串行融合和并行融合［14］。特征融合流程图如图4所示。

图4 HOG-PCA特征与LBP特征融合流程图

设在样本空间Ω上存在两个不同的空间A、B，对于任意模式样本ε∈Ω，其对应的两个特征向量分别为α∈A何 β∈B，串行融合后的特征矩阵为 γ=(α ，β ) 。 并 行 融 合 后 的 特 征 矩 阵 为γ=α+iβ ，其中i为虚数单位。

串行特征向量的计算过程如图5所示，分别计算将LBP特征直方图和HOG-PCA特征直方图，串行连接形成联合直方图。

图5 联合直方图

2.5 分类器训练

在分类器算法中，应用比较广泛的是线性SVM和Adaboost算法。支持向量机（SVM）是近些年发展起来的一种有监督的学习模型［15］，在解决小样本、非线性和高维模式识别中具有许多优势。SVM采用核函数将输入的数据x映射到一个高维特征空间，然后在高维空间求广义的最优分类面，而原本在原空间不能线性可分的数据，就可以在高维空间进行线性分类。本文采用了线性SVM分类器训练。

3 实验与分析

3.1 实验环境

本试验的平台为Visual Studio 2010，使用Opencv 2.4.9的库资源。计算机安装Win7系统，配置i3处理器，主频3.5GHz，内存4G。训练集由6种手势，如图6所示。每种手势55张训练样本组成，实验测试图像大小为64*64。手势样本中背景复杂多变，所以适应性更强。

图6 识别的六种手势

3.2 实验过程

本文采取HOG特征、HOG-PCA特征、LBP特征以及本文的HOG-PCA+LBP融合特征，结合SVM分类器进行训练。对于HOG特征降到多少维是最合适的，本文将通过具体数据来确定。在实验中尝试取多个主成分值并对比，实验结果如表所示，表1是提取HOG特征不降维的情况下各个手势的识别率，平均识别速度为13.3ms；表2是提取LBP特征下各个手势的识别率，LBP特征维数为144维，平均识别速度为2.5ms；表3是选取手势B，运用PCA降维HOG特征后不同维数的识别率和识别速度；表4是HOG-PCA+LBP融合特征在不同维数的识别率和识别速度。

表1 提取HOG特征的识别率

分析表格可知，直接提取HOG特征时识别率高，但由于特征维数多，所以耗时多；LBP特征耗时少，但识别率不太理想；PCA-HOG特征可以在保持一定的识别率的同时识别速度也有了较大的提升。基于本文的将LBP特征与PCA-HOG特征融合的方法，识别率更优于PCA-HOG特征，却识别速度与PCA-HOG保持一致。融合特征在维数为164维时识别率和识别速度是最理想的，在维数更低或更高的情况下，识别率都保持大致不变，识别速度却大幅提高。

表2 提取LBP特征的识别率

表3 PCA-HOG的维度与识别率和识别速度关系

表4 HOG-PCA+LBP融合特征的维度与识别率和识别速度关系

4 结语

本文分析了图像分类的一般原理及步骤，并提出一种简单高效的分类方法，将PCA-HOG特征和LBP特征相结合，既获取了手势的梯度信息又获取了手势的纹理信息。实验结果表明，此方法在保证准确性的同时实时性上也有明显的提高。实验表明，本文提出的方法可以达到较好的识别效果。