一种面向航空集群的集中控制式网络部署方法

吕娜，刘创，陈柯帆，曹芳波

空军工程大学 信息与导航学院，西安 710077

近年来，随着飞行器的更新换代，尤其是无人机的迅速发展，航空平台的信息化、智能化水平不断提升，推动了空中作战模式的改变。为了使多个航空作战平台实现综合化、体系化作战，研究人员将生物集群的理念应用到航空作战领域，提出航空集群的概念[1-3]。航空集群作战为了实现多平台间战术协同和平台能力优势互补，需要依托机载网络将大规模空中平台灵活组网。

当前，以航空数据链和航空自组网为代表的机载网络一直遵循着传统分布式网络架构的设计思路[4]。通过不断升级网络设备的各种软硬件虽然能够一定程度上保证网络性能的提升，但是这种“打补丁”的方式效率很低，不仅使得网络变得更加臃肿，也使得网络管理与配置过程复杂且僵化，导致网络服务能力扩展和升级变得十分困难，难以保障未来航空集群各成员间的灵巧作战协同。

软件定义网络(Software Defined Networking，SDN)的出现为传统分布式网络的发展带来了全新的研究思路，它使网络控制平面与数据平面分离，通过逻辑集中控制的方式对网络设备进行统一管理[5]。与传统网络相比，SDN具有更高的灵活性、更强的可编程性和更大的开放性。SDN在小型数据网络中已经得到了广泛应用，但是随着SDN在大中型网络中的应用，控制平面的健壮性和可扩展性面临着重要挑战[6]。

从网络演进的角度看，SDN的灵活性、开放性、可编程性等优势正好可以弥补现有机载网络在航空集群作战应用背景下存在的弊端，具有较好的应用前景。目前相关的研究已经展开，如文献[7-8]均指出SDN网络范式应用于机载网络能够带来众多优势。文献[9]在总结航空集群作战特点和SDN设计思想的基础上提出了软件定义航空集群机载战术网络，并对其基本网络架构进行阐述。但是这些研究的内容主要聚焦在概念和基本网络架构描述，缺乏深入的理论建模分析。在航空集群环境下由于节点的高移动性和航空信道的不可靠性等因素使得控制器难以像地面网络一样与网络节点有效可靠地交互信息，这对控制平面的健壮性和可扩展性提出了更大挑战。而如何在航空集群作战环境下，构造符合网络需求的控制平面，解决大规模及动态网络下控制平面可扩展性差的问题，是实现SDN范式在机载网络中实际应用的重要前提。

为了解决单一控制器的性能瓶颈和单点失连问题，提高网络的可扩展性，多控制器的架构被普遍采用。现有的多控制器架构主要分为3类[10]：扁平式体系结构如Onix、Ethane,垂直架构如Kandoo、Logical xBar等，和以Orion为代表的混合层次式体系结构。在多控制器的架构下，研究人员发现控制器的部署位置和数量会直接影响到控制层面的性能，近年来针对控制器部署问题(Controller Placement Problem，CPP)的研究逐渐成为研究热点[11-12]。控制器部署是实现控制平面构建的基础和前提。在网络拓扑动态变化和网络连通性不稳定的机载网络中，控制器的位置不仅会影响到新流建立的时延，而且会直接影响到网络的配置和管理效率和网络的可靠性等方面。因此，在以航空集群为背景的集中控制式网络中对控制器部署问题进行研究，提出合适的优化模型和求解方法，对于提升网络性能具有重要意义。

前期对于CPP的研究背景主要集中在地面有线SDN，研究内容主要集中在性能尺度以及搜索算法两个方面。文献[13]首次提出控制器放置问题，指出CPP问题求解的关键点是控制器数量和控制器在网络拓扑中的位置，同时作者阐述了不同控制器部署方案对网络时延性能的影响。在此基础上，文献[14]提出了可靠性优化的控制器部署问题，并针对这一问题提出了相应的贪心算法和模拟退火算法进行求解。除时延和可靠性外，控制器的负载均衡及网络弹性和容错性也是求解CPP问题考虑的重要性能尺度。文献[15]针对控制器的负载均衡问题，首次提出容量限制的控制器部署问题(Capacitated Controller Placement Problem, CCPP),并针对这一问题提出基于K-center的启发式算法，求解满足控制器容量限制的最小控制器数量。上述研究主要针对扁平式的控制器架构，没有考虑层次型控制器部署的需求。文献[16]针对层次型多中心SDN控制器部署问题，通过减少图划分的域间割边数以降低SDN跨域流数量来提高流表构建效率。文献[17]在综述已有研究的基础上，也指出未来对CPP的研究应从实用性角度出发设计求解方法，以便指导同类或相似的网络场景中CPP的求解。

可以看出，现有CPP的研究主要面向固定拓扑的地面有线网络，没有考虑到动态拓扑下无线网络的部署需求。由于机载网络与地面有线网络的巨大差异，如在控制器架构上，受高动态的网络拓扑和频繁的链路中断影响，以往CPP研究基于的扁平式多控制器架构就难以适用于航空集群场景，同时针对地面网络所设计的性能尺度和搜索算法也不能符合航空集群的优化需要。因此在航空集群背景下对CPP研究，应该在总结网络场景需求特点的基础上，结合控制器架构设计符合实际应用的性能尺度选取和求解算法。而目前相关研究由于缺乏这些考虑，在实际应用时很难有较好的指导意义。

针对上述问题，本文从航空集群控制平面的可扩展性出发，研究了混合层次式的多控制器架构及其部署问题。在提出适合航空集群的控制器架构基础上，将传统的多控制器直接部署转化为子域划分和域内部署两个步骤。提出了基于节点密度排序(Node Density Ranking, NDR)的子域划分算法。考虑到控制器的负载均衡，对NDR扩展提出了容量限制下(Capacitated Node Density Ranking, CNDR)的子域划分算法。考虑到网络的动态特性，从网络整体性能角度选取控制链路的平均时延和平均失连率作为优化目标，在子域划分的基础上提出了改进的Pareto模拟退火(Improved Pareto Simulated Annealing，IPSA)对多目标优化问题求解。

1 模型设计

1.1 场景及控制器架构描述

本文讨论是基于如图1(a)所示的集群作战应用场景，该场景中存在预警机、战斗机、侦察机、无人机等多种类型的作战平台，它们依据作战阶段的不同任务动态组织。与传统SDN应用场景不同，在航空集群环境中，网络节点的移动性使得控制器与控制域内传输节点的稳定互联变得十分困难；高对抗的战场环境使得控制器存在较高的失连风险；无线链路的不可靠性使得扁平式控制器架构难以实现多个控制器之间及时有效的信息共享；基于上述考虑，为实现对集群平台的有效网络管控和提高网络的可扩展性，航空集群环境中应采用混合层次式控制器架构实现对网络的逻辑集中控制。

文献[18]提出了一种用于大规模网络的混合层次式控制器架构，本文在此基础上，考虑到航空集群的特殊应用场景，做出以下设定。航空集群环境下的混合层次式控制器架构如图1(b)所示，考虑到网络规模，本文将控制平面分为两层。顶层由全局控制器(Globe Controller，GC)组成，GC负责跨区域流量计算和转发。由于航空集群平台能力之间存在较大差异，GC应该部署于预警机、指通机等生存能力和综合信息处理较强的平台之上，GC之间通过定向天线对各自负责区域内收集到的网络视图信息进行交互，进而形成掌握全局网络信息的主控制平面。主控制平面从全域战场的视角对整个航空集群网络进行管控，具有最高的控制优先级。

底层由本地控制器(Local Controller，LC)组成，其仅具有自身控制域内的本地网络视图信息，向上与GC共同维护全局网络视图，向下负责管理本地设备和本地流量的转发。LC是根据网络节点规模和分布、网络流量等情况按需部署在集群平台上的。由于其与平台内的网络设备共用底层物理硬件资源，可以根据网络变化情况在相应平台上开启或者关闭本地控制器，实现对本地网络设备的弹性管控。动态变化的本地控制器形成本地控制器资源池，与全局控制器共同形成控制逻辑集中的航空集群网络的控制平面。本文只对该控制器架构进行简要概念描述，重点研究该架构下本地控制器的部署问题。

1.2 问题建模

在上述混合层次式控制器架构下，本文研究内容为在已知网络节点和全局控制器数量和位置的情况下，求解满足网络管理的性能需求时的LC控制器数量和部署位置。

考虑到实际部署SDN时，传统分布式网络和SDN是共存的，控制器部署是按照覆盖网(overlay)方式，即在原有网络基础上部署一个逻辑控制层面[19]。针对部署场景做以下假设：

1) 网络中每个节点代表一个交换机，本文统称为传输节点，控制器为co-located部署方式，即控制器和交换机可以部署于网络同一节点，此种情况下认为两者的传输时延为0。

2) 除GC之间单独配置定向链路共享网络视图信息，其他控制路径均为带内(in-band)方式，即控制信息和数据信息走相同路径，不单独部署控制信道。

3) 网络中每个交换机在同一时间只能由唯一的LC控制，每个LC也只能由唯一的GC控制。

为形式化地描述本地控制器LC部署问题，将网络建模成一个无向图G=(V,E,S,M)，其中V={v1,v2,…,vq}代表拓扑中网络节点集合，q为拓扑中节点数量;E={(vs,vt|vs,vt∈V)表示网络节点之间链路的集合；M={m1,m2,…mm}表示全局控制器集合;S={s1,s2,…,sk}表示本地控制器集合，其中S⊆V且M⊆V；定义传输节点与LC的连接矩阵G=[xvs]|V|*|S|和LC与GC之间的连接矩阵H=[ysm]|S|*|M|，xvisj=1时，说明节点vi属于控制器sj的控制域下，反之则为0。相应的ysimj=1时，表示LC节点si属于GC节点mj的控制域下。

2 子域划分算法的设计

航空集群执行任务过程中，网络拓扑结构相对保持稳定。作战任务改变，网络拓扑结构发生变化。在航空集群环境下，应当由掌握全网视图信息的全局控制器根据网络环境变化运行LC部署算法得到部署结果，并将LC启动信息在全网广播。根据该信息，网络中的相应节点启动控制器模块成为LC。

从上述部署流程中可以看出，LC资源池的方式使得控制器部署可以灵活适应网络拓扑结构的变化，有利于对本地网络设备的弹性管控。但这也给CPP算法的设计提出了较为苛刻的要求。首先集群构型的改变具有时间限制；其次航空集群规模通常较大，平台数量一般能达到上百架以上。对于CPP的求解是NP难问题，当网络规模达到上百个时，根据使用算法不同，求解时间最大能够达到几个小时。为防止在大规模动态网络环境下求解CPP时间过长导致LC部署无法完成，本文算法的设计重点是在简化算法时间复杂度并保证解的精确性基础上，求解出较优的LC部署方案。

2.1 基于节点密度排序的子域划分算法

为了区分节点在网络中的位置，本节首先引入两个定义，邻居密度ρi和最短距离δi。

定义1节点的邻居密度ρi为

(1)

式中:Dij为节点si和节点sj之间的实际距离;Dc为距离阈值，函数Γ被定义为

(2)

从式(1)中可以看出节点的邻居密度仅与Dc的取值有关。由于不同拓扑构型的网络节点邻居密差异较大。在相同拓扑下，阈值越大，计算越复杂，而阈值越小，难以有效区分不同节点的邻居密度。因此，本文设置Dc为

Dc=0.3max(Dij)

(3)

定义2节点最短距离δi为

(4)

根据定义一个具有较大ρi和δi值的节点，更有可能成为子域的顶点。对于在一定区域内随机分布的节点，为了找到子域的顶点，首先根据定义计算每个节点的邻居密度ρ和连接距离δ。然后分别根据ρ值和δ值对节点排序，将排序号相加得到节点的总排序号，按照总排序号值和LC数量k得到区域顶点集Scon。最后按照到区域顶点距离最短的原则将网络节点划分为k个子域。算法1给出了NDR的描述细节。

算法1基于密度排序的子域划分算法NDR

输入：节点位置，LC数量k

输出：子域集N

1) for eachs∈Sdo

2) 根据式(1)和式(4)分别计算每个节点的pi和δi3) end for

4) 将节点集V分别按照p值和δ值降序排列得到V1和V2

5) 记录每个节点的对应排列序号i和j

6) 将每个节点的p值排列序号i和δ值排列序号j相加，得到总排列序号

7) 将节点集V按照总排列序号值升序排列得到Vcon

8) 取前k个点形成区域顶点基Scon

9) for eachs∈Sdo

10) 计算每个节点到区域顶点的距离

11) end for

12) 按照距离区域顶点距离最短的原则，将网络分成k个子域N={N1,N2,…,Nk}

2.2 控制器容量限制下的子域划分算法

上述对子域的划分没有考虑控制器容量的限制，无法得到符合网络需求的控制器数量，实现对CCPP问题的求解。对于逻辑集中控制的机载网络，控制器的数量对网络性能有着重要影响。因为在集群作战过程中，平台多以编队云的形式执行作战任务。属于同一编队云的作战单元空间跨度较小、信息交互需求较高。将同属于一个编队云的节点放到同一本地控制域下，可以有效减少对GC的访问降低流表建立的开销和时延，因此子域数量应该尽可能小。但是子域数量对应于需要部署的LC数量k，当k值过小时，本地控制器负载将会失衡，这将严重影响控制器的控制效能。综合以上考虑，本文将考虑控制器容量的LC部署问题定义为满足网络负载性能要求的最少LC数量。

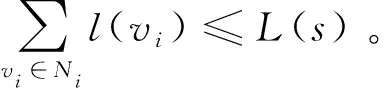
算法2给出了容量限制的子域划分算法CNDR。首先，根据算法1得到区域顶点集Scon。然后，根据Scon中节点排序情况，依次选取序号靠前的节点作为子域顶点，形成多个子域，计算每个子域的LC负载情况。最后逐渐增加子域规模直到求出所有子域都满足负载均衡要求时的最小k值。

为了评估多个子域之间的负载情况，文献[20]定义了负载均衡指数B，其表示子域间交换机提交的平均信息量之和的最大差值。需要说明的是，由于航空集群的特殊环境，部署结果发送到相应节点时间周期较长。而请求信息量是动态变化的，算法2使用的节点平均信息量只能通过预测或统计来大致判断子域的负载情况。

(5)

算法2容量限制的子域划分算法CNDR

输入：节点位置，网络负载均衡指标

输出：子域N,LC数量k

1) 首先根据算法1的1)～7)行，得到按照总排列序号值排序的Vcon

2) fori=1:n

3) 取Vcon中前i个节点作为顶点

4) 按照距离区域顶点距离最短的原则，将网络分成i个子域

5) 根据式(5)计算每个区域内的负载情况

7) 返回此时的i值和分域情况N

8) break

9) end if

10) end for

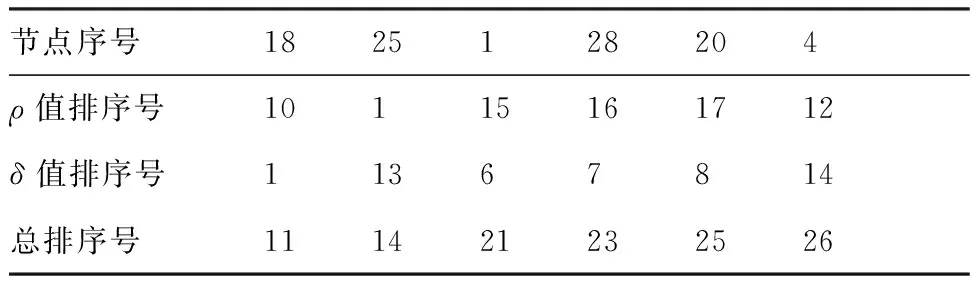
为了说明CNDR-DPA算法的计算过程，在400 km×300 km的区域随机部署36个节点，对节点编号，节点分布如图2(a)所示。设置节点的通信半径R=80 km。根据算法1的1)～7)行，得到按照总排列序号值排序的Vcon，表1为Vcon总排序号靠前的部分节点排序情况。假设每个节点的流表策略配置需求l(v)相同，本地控制器的额定负载L(s)=t×l(v)。当t为9，并取至Vcon的第5个节点时，计算所有子域的负载情况,均满足额定负载要求，此时网络将以节点{18,25,1,28,20}为子域顶点，按照最短距离优先原则将节点分成5个子域，得到节点分区结果如图2(b)所示，分别用5种不同形状的点表示。

节点序号1825128204ρ值排序号10115161712δ值排序号 11367814总排序号 111421232526

3 域内LC的部署优化

3.1 优化性能指标

将网络节点划分成多个子域后，需要根据网络性能尺度和搜索算法找到控制器在每个子域中的适当位置。由于航空平台的动态移动性和网络状态的时变性，本文在LC部署过程中从网络的整体性能角度出发，考虑到混合层次式的控制器架构设计了以下两种性能尺度。

1) 控制路径平均传播时延

网络的控制路径平均传播时延反映的是网络中控制路径传播时延的整体情况。在大尺度分布的航空集群应用场景下，网络的发送时延、排队时延和处理时延相对于传播时延小很多，传播时延为整个通信时延主要的影响因素。控制路径的平均传输时延包括交换机与LC间平均传播时延和LC与GC之间的平均传播时延，它严重影响控制平面对网络事件的响应速度和管控效率。本文将控制路径的平均传播时延定义为传输节点到LC间平均传输时延和LC与GC之间的平均传输时延之和：

(6)

式中：d(vi,sj)为传输节点vi及LC节点sj之间的最短路径时延集合；d(si,mj)为LC节点sj与GC节点mj之间的最短路径时延集合。

2) 控制路径平均失连率

在逻辑集中控制式的网络中管理和控制网络的命令是通过控制路径传输的，控制路径的可靠性直接关系到整个网络的可靠性。由于航空链路质量的不稳定性，控制链路出现容易出现中断现象，同时在战场环境下传输节点具有较高的失连概率。文献[21]已经做出了关于网络可靠性的研究工作。在这里，为了对网络控制路径的可靠性进行评估，本文定义控制路径的平均失连率，它是指控制路径失去连接概率的均值，包括交换机与LC失连概率和LC与GC失连概率。设控制链路中断率为d1和传输节点失效率为p1，则控制路径平均失连率为

(7)

式中：l∈(V,S)为传输节点到LC节点的控制路径集合；l∈(S,M)为LC节点到GC节点的控制路径集合。

3.2 域内LC部署算法

本文对每个子域内LC的部署位置求解过程中以最小化控制路径平均传播时延和控制路径平均失连率为目标，这是一个多目标优化问题。由于多个目标之间存在冲突，因此多目标优化最终得到多个Pareto解。

以往对于CPP的求解主要考虑的是域内的性能尺度，因此在子域划分完成之后，可以通过逐个子域进行遍历搜索的方式求解到控制器在每个子域内合适的位置。而本文设定的优化目标考虑的是控制链路的整体性能，LC的位置是相互影响优化目标的，因此必须从整个网络的角度来求解出控制器在每个子域内的部署位置，但这也显著增加了计算的复杂度。

对于多目标优化问题求解的时间复杂度和精确性取决于所选取的算法，为了在有限时间内搜索出精确结果，本文采用Pareto模拟退火(Pareto Simulated Annealing，PSA)算法。PSA算法是基于蒙特卡罗迭代求解法的一种多目标启发式随机搜索算法，实现简单、计算效率高，通过合理的参数设置可以在计算时间和解的精确性之间权衡，具有较高的灵活性。

根据以上分析，利用算法1或算法2对网络节点分区后，需要在每个子域内部署一个控制器。为了满足LC部署问题需求和求解方便，本文对PSA算法进行改进(IPSA)，算法3中描述了求解流程，有如下关键步骤：

1) 种群个体初始化。算法中的种群个体是由k个元素构成的向量X，k为LC节点的数量。PSA算法通常会采用完全随机的初始种群，这种方法虽然能够保持较好的种群多样性，但是容易生成适应度差的个体，不利于算法收敛。本文设置初始种群为子域顶点集Sopt，这样邻居密度更高的节点成为初始种群可以有效节省PSA算法的初始运行时间，提高精度。

2) 目标函数权重。合理的目标函数权重可以保证产生的解具有良好的多样性。PSA算法在每迭代过程中用一系列产生样本的解来控制目标函数权重的大小。如果x第一次迭代或者没有一个最靠近样本x的非劣解x′，则设置权重为随机值且满足∀λi≥0，∑λi=1；否则，则设置每个目标函数fi的权重为

(8)

式中：α>1。

4) 接受概率P。PSA算法的接受概率与权值大小有关，通过对权值大小的控制可以增加或降低某个目标的接受概率。PSA是以概率P接受新解。

(9)

算法3基于改进PSA的域内LC部署

输入：G=(V,E)，Sopt，k，m，初始温度T0，降温系数p

输出：Pareto解集M，LC部署位置

1) 初始化目标权重λi,T=T0

2) 初始解X=Sopt，计算所有目标函数值并加入Pareto解集M中

3) whileT>1 do

4) 产生邻域解Y，并计算其所有目标函数值

5) 比较新产生的邻域解Y与Pareto解集M中的每个解并更新Pareto解集M

6) 根据式(8)和式(9)分别计算权重λi和接受概率P

7) 如果Y未进入Pareto解集M，以概率P接受Y，如果新解被接受，则令其为X，如果新解未被接受，则保留当前解

8) if 完成m次迭代 then

9)T=Tp

10) end if

11) end while

4 实验结果及分析

4.1 仿真环境及参数说明

对于实验的相关环境和参数作出如下说明：

1) 在一台主频为3 GHZ、内存为8 GB的PC上，基于MATLAB环境下对本文算法进行仿真。

2) 由于目前尚不存在实际应用的具体参数作为参考，为简化实验过程作出以下假设：所有本地控制器都有相同的负载容量、处理能力等；所有的传输节点向控制器提交的请求信息量相同，设l(vi)=1；单个节点和链路的故障率为区间[0,0.04]和[0,0.08]之间的随机数；值得说明的是，这种参数设置仅影响具体的计算值，并不影响对算法正确性的验证，实际应用时可根据全局控制器掌握的具体参数信息进行计算。IPSA算法的具体参数在4.4节实验中根据节点数量进行设置。

3) 本文算法并不考虑GC的数量和位置对网络性能的影响。因此规定在实验过程中，节点数量小于100时，GC数量为1。节点数量大于100时，GC数量为2。GC的部署位置为随机指定的节点。

4) 考虑到航空集群中各作战单元依据作战动态组织，在网络拓扑上表现为随机动态变化。为了体现这一特点，实验中使用的拓扑是在给定区域内随机生成多个节点，利用Dijkstra算法得到任意两点间的最短路径方式获得的。实验中设置网络节点分布区域的大小为700 km×600 km，节点的通信半径R为120 km。

由于在相同节点数量下，不同网络拓扑结构的网络性能具有一定差异。为了验证本文算法在不同网络节点规模下的有效性和适用性，实验过程中将相同节点数量作为一种实验条件，为了排除节点位置变化对算法验证的影响，对比的性能指标是相同实验条件下得到不同网络拓扑结构性能优化结果的均值。具体实验次数和网络拓扑数量在各小节实验中说明。

为了综合评估本文算法的有效性，在实验过程中，选取3种解决大规模SDN控制器部署问题的算法作为对比，3种算法的主要描述如表2所示。第1种是基于社团发现的控制器部署算法。第2种是以K-means代表的聚类问题求解算法。第3种是将启发式算法引入到CPP问题求解。前两种算法为降低时间复杂度，都采取了子域划分域内部署控制器的设计思路。

表2 对比算法描述Table 2 Description of comparison algorithms

4.2 NDR划分算法分析

为了验证NDR对网络节点的子域划分情况，分别在节点规模为60、100、140的航空集群网络环境中，每个节点数量下随机生成10个拓扑，比较不同节点规模下的负载均衡指标随控制器数量变化情况，并以LPA和K-means算法作为对比。对于LPA和K-means算法，因为子域划分过程带有随机性，因此实验结果采用多次仿真取平均值的方法。

实验结果如图3所示，子域划分LPA和K-means算法的子域规模不可控，负载均衡指数波动较大，且远远高于NDR算法，因此极易出现控制器负载不均衡的情况。3种子域划分算法在计算过程中都没有对控制器容量进行限制，LPA算法利用节点标号在网络中任意传播直至收敛来进行子域划分，K-means算法是通过迭代计算将节点按照最小时延划分为K个类别，而NDR算法在划分子域过程中主要考虑周围节点的密度和网络节点的分布情况，因此可以获得更优的负载均衡指数。需要说明的是，本节仅比较了不同算法的子域负载均衡指数，实际上控制器的负载状况不仅与子域规模有关，也与控制器在子域中的位置相关。实验也表明，利用NDR算法将网络划分多个子域，可以有效限制子域规模之间的差距，对实现控制器的均衡具有良好效果。

4.3 CNDR划分算法分析

为了验证CNDR算法对于CCPP求解的有效性，本节在节点规模从50～200的区间里，随机生成100个网络拓扑，使用CDNR算法计算每个拓扑在具有相同控制器容量限制下所需的最小LC数量。本文使用文献[15]提出的求解CCPP问题的K-center算法作为对比。K-center算法是一种基于启发式的随机搜索算法，通过迭代寻找满足控制器负载均衡的K个中心，来求解出网络所需的控制器部署数量和位置。实验中，每个传输节点向LC提交的请求信息为[0.5,1.5]之间的随机数，但所有传输节点向对应LC提交的请求信息总量为N，N为节点数量。实验结果如图4所示，x轴表示LC数量，y轴表示满足控制器负载均衡的拓扑在所有拓扑中所占比例。

从图4中可以看出，使用CNDR算法,当控制器个数超过10时，50%以上的拓扑能够满足控制器容量的要求;当控制器个数达到20时，所有的拓扑都可以满足控制器容量的要求。而使用K-center算法，需要的控制器数量为15～26个。实验结果表明，使用CNDR算法相比于K-center算法求解所需的控制器数量更少，求得CCPP问题解的质量更高。这是因为本质上K-center是一种启发式搜索算法，主要思想是通过反复迭代找到满足控制器容量限制的K个中心。在节点数量较多的情况下，K-center算法容易陷入局部最优解。而CNDR算法只需数学计算即可，不会陷入局部最优。

4.4 IPSA性能分析

为了评估IPSA算法的优化性能，本节设置场景中的节点个数为80，LC数量为k=6，在子域划分基础上，以控制路径的平均传播时延Tavg和平均故障率σavg作为目标函数，对LC部署进行优化。为了在求解精度和求解时间之间权衡，根据网络节点规模，设置IPSA中迭代次数m=30，初始温度T0=150，降温系数p=0.90。实验过程中使用穷举算法(Brute Force，BF)对子域间所有解的组合进行遍历搜索，寻找问题最优解，作为对比验证IPSA算法在求解精度上的损失和计算时间上的优势。

首先重复实验100次，验证IPSA算法的稳定性，记录Tavg和σavg的取值情况。图5为100次实验平均传播时延和平均失连率的取值情况变化，图中横线为使用BF算法得到的最优值。Tavg在[0.807,0.887]内波动，波动幅度为±2.36%；σavg波动区间为[0.122,0.135]，波动幅度为±1.36%。

表3给出了BF、IPSA和PSA 3种算法的平均性能比较。3种算法都是在利用NDR算法进行子域划分的基础上进行优化求解的。从表中结果可以看出，通过改进的PSA算法——IPSA算法具有更高的稳定性，且更接近最优解。

表3 100次独立实验平均性能比较

图6为采用IPSA、POCO、PSA和BF算法获得的Pareto解最优前沿。从图中可以看出，控制路径平均失连率和平均传输时延成反比。相比于PSA算法和POCO算法，IPSA算法得到了较为平滑且均匀的Pareto面，且解更接近BF算法得到的结果。注意图中给出的Pareto解为满足优化目标的一组权衡解，实际的控制器部署过程中应该根据网络性能需求，从Pareto解集中选择合适的方案。

4.5 本文算法的优化性能分析

本节利用LPA、K-means、POCO和本文所提的NDR和IPSA算法(以下用NDR-IPSA统一表示)对LC部署优化性能进行验证。节点规模为100，对比算法的迭代次数均为200次，IPSA算法参数中m=20，初始温度T0=100，降温系数p=0.95。首先，验证LC数量对网络性能的影响。图7和图8分别给出了在不同LC数量下控制路径的平均传播时延Tavg和平均失连率σavg，实验数据为各算法重复计算50次的平均值。

从图7和图8均可以看出，随着LC个数的增加，平均传播时延Tavg和平均失连率σavg均逐渐降低。其中，Tavg平均降低了46.7%，σavg平均减少了24.8%。因此，在航空集群集中控制式的网络中增加本地控制器的数量可以有效减少控制链路的平均时延和平均失连率。对比其他3种算法，POCO优化性能更好，这是因为当划分子域过多时域内节点数量将变少，这直接限制了算法的优化能力。而与本文算法在子域划分中仅考虑节点邻居密度不同的是，K-means是根据预先定义的优化目标进行子域划分的，更具灵活性，在子域数量较多的情况下优化性能也好。

图9为4种算法的计算时间随LC数量变化情况，可知LPA和K-means算法随着LC数量的增加，计算用时平稳增长，增长幅度较小。而POCO随着LC数量的增加，计算用时显著增长，增长幅度较大。与这3种算法不同，本文算法的计算用时快速减小。这是因为随着LC数量增加，子域数量也在增加，IPSA算法的搜索空间逐渐减小。LPA和K-means是基于迭代的子域划分方法，因此在网络规模一定的情况下，子域数量增多反而增加了时间复杂度，而NDR-IPSA算法只需要一次计算就可以实现网络区域的划分。

图10给出了在不同节点数量下计算时间的对比情况。随着节点数量的增加，4种算法的计算时间都在增加，其中POCO算法计算时间远高于LPA、K-means和本文算法，在节点数量为120以上时POCO的平均计算时间是本文算法的6倍左右。可以看出，与使用启发式算法的POCO表现不同的是，使用子域划分域内部署控制器的方式可以显著降低大规模SDN控制器部署的时间复杂度，但是结合图7和图8的仿真可以看出，这种方式也损失了解的精确度。对比可知，本文所提算法更适用于大规模网络及动态拓扑环境下的控制器部署问题。

5 结 论

1) 针对航空集群的特殊环境，通过扩展控制层级和定义本地控制器资源池的方式，使得控制器部署可以灵活适应网络拓扑的变化，增强了网络的可扩展性。

2) 为了满足本地控制器快速部署需求，针对航空集群环境下节点规模大、计算复杂度高的问题，提出了NDR和IPSA算法，通过仿真验证了本文算法提升网络性能的有效性和在大规模网络及动态拓扑环境下的适用性。

3) 考虑到控制器的负载均衡，为了求解出网络需要的控制器数量，对NDR扩展提出了CNDR，并通过仿真验证了该算法对于解决CCPP问题的有效性。