基于DP-SA的机载外辐射源无源协同定位

郭云飞，张沛男, 才智

1.杭州电子科技大学 自动化学院，杭州 310018 2. 中国电子科技集团公司 第二十八研究所，南京 210007

机载外辐射源无源协同定位(Airborne Passive Coherent Location，APCL)是一种新体制无源协同定位技术[1-4]。利用我方/敌方/第3方的预警机/无人机作为机载外辐射源对目标进行无源定位，不仅具有传统无源协同定位(Passive Coherent Location，PCL)的隐身/反隐身、低成本、部署灵活等优势，还因外辐射源的可移动性，扩展了探测范围，提升了探测系统的灵活性，近年来在雷达探测领域引起了高度关注[1-2,5-10]。

文献[1]从认知雷达的角度，首次提出了基于可移动外辐射源的无源协同定位概念。文献[2]系统分析了外辐射源位置未知时的PCL系统可观性，提出一种递推的航迹起始/维持算法，并推导了最优理论性能界。国内对APCL的研究主要集中在信号处理前端，初步构建了外辐射源可移动的接收系统[5]，设计了机载外辐射源条件下的距离徙动校正方法[6-7]和恒虚警检测方法[8]。然而机载外辐射源在提升系统探测灵活性的同时，其可移动性也为无源协同定位带来新的挑战。当机载外辐射源非合作时，由于其准确位置难以获取，会大幅降低APCL的检测跟踪性能[2]。APCL系统在机载外辐射源位置不确定条件下的目标检测与跟踪问题，本质上类似于传感器位置不确定下的目标检测与跟踪问题[2]。文献[9]提出了状态扩维(State Augmentation，SA)算法，降低了传感器位置不确定对目标跟踪精度的影响，文献[10]给出了一种传感器位置不确定时目标跟踪的闭式代数解。然而上述两种算法仅适用于低杂波或无杂波的探测环境[9-10]，在强杂波探测环境下，两种算法均无法保证实时性[2,10]。

当测量方程非线性且机载外辐射源位置不确定时，为了解决强杂波背景下无源协同定位问题，本文提出一种基于动态规划状态扩维(Dynamic Programming-State Augmentation, DP-SA)的无源协同定位方法，该方法耗时少，能保证实时性。DP-SA方法共由动态规划(Dynamic Programming,DP)和SA两部分组成。首先，考虑到传统DP的状态转移范围只适用于线性测量系统，本文利用误差传播理论，在APCL的非线性测量空间内，推导外辐射源位置不确定时DP的状态转移范围。其次，根据极值理论(Extreme Value Theory, EVT)确定回溯阈值，再通过状态回溯提取源于目标的测量值序列。最后，通过SA技术将目标状态扩维，使之包含外辐射源状态，利用提取的测量值序列对扩维状态进行非线性滤波，实现目标状态与外辐射源状态的联合估计。

1 问题描述

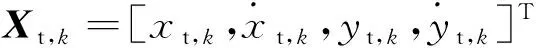
Xk+1=Fk+1Xk+wk+1

(1)

在强杂波环境下假设APCL系统在第k帧共收到Mk个测量，其测量集合Zk为

Zk={zk(i)=(rk(i),θk(i),Ak(i))|1≤i≤Mk}

(2)

式中：zk(i)为第k帧源于目标或杂波的第i个测量，又被称为第i个候选状态[12-13]；rk(i)为双基站距离；θk(i)为回波路径相对于直达波路径的方位角[1]；Ak(i)为回波幅值。

含噪的rk(i)和θk(i)的测量方程为

(3)

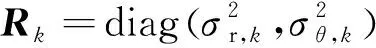
hr,k(i)和hθ,k(i)的具体公式为

(4)

Ak(i)的测量方程为[14]

(5)

hA,k(i)=

(6)

式中：B和C分别为等效椭球体的长轴和短轴半径；S1为外辐射源功率密度；βk为双基站角，即[14]

βk=

(7)

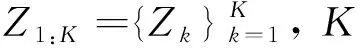
2 基于DP-SA的APCL技术

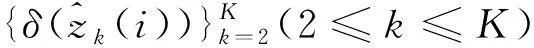
首先，考虑外辐射源位置的不确定性，基于误差传播理论，在非线性测量空间(即候选状态空间)构建DP的状态转移范围。其次，根据幅值测量值构造值函数[12-13]，在每个测量值(候选状态)的状态转移范围内寻找相邻帧中最大的值函数进行递推幅值积累。再次，基于极值理论离线计算DP的航迹回溯阈值，进而获得目标状态序列在非线性测量空间的映射。最后，对目标状态扩维，

使之包含外辐射源状态，利用上述映射序列对扩维状态进行非线性滤波，实现目标状态与外辐射源状态的联合估计。

2.1 非线性测量空间状态转移范围

(Δrk)2=(Δxk)2(∂rk/∂xk)2|xk=ε(zk(i))+

(8)

(Δθk)2=(Δxk)2(∂θk/∂xk)2|xk=ε(zk(i))+

(9)

ε(zk(i))=

(10)

η(zk(i))=

(11)

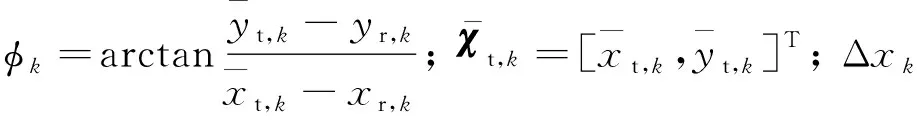
2.2 幅值积累和基于EVT的门限状态回溯

zk(i)的幅值积累函数记为I(zk(i))。

步骤1初始化：当k=1时，遍历所有候选状态z1(i)，令I(z1(i))=A1(i),δ0(z1(i))=0。

步骤2幅值积累：当k>1时，遍历第k帧候选状态并进行幅值积累。幅值积累过程为

(12)

(13)

式中：Ψk-1(zk(i))为可能转移到zk(i)的第k-1帧候选状态的状态转移范围。对于Ψk(zk-1(j))内没有第k帧候选状态的zk-1(j)，可利用动态模型预测其第k帧的状态zk(i)。

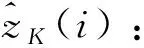
(14)

根据极值理论[20]，单帧杂波幅值的极大值服从Gumbel分布，杂波幅值关于虚警率PFT的函数为

(15)

(16)

(17)

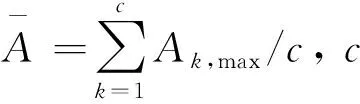
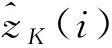
2.3 基于状态扩维的目标-外辐射源联合估计

外辐射源位置不确定时，系统的等效观测噪声协方差会增大，其修正公式为[21]

(18)

式中：Ht,k为hk(i)关于外辐射源状态Xt,k的雅克比矩阵，具体表达式为

(19)

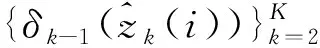
1) 目标和辐射源预测

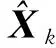
(20)

(21)

2) 目标-外辐射源状态联合估计

(22)

(23)

PA,k+1≜diag(Pk+1,Pt,k+1)=PA,k+1|k-

Kk+1Hk+1PA,k+1|k

(24)

式中:Hk+1表示hk+1(i)关于目标状态和外辐射源状态的雅可比矩阵，即

(25)

3 仿 真

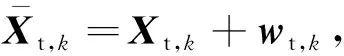
3.1 目标存在

图2分别给出了20帧距离差、方位角和回波幅值的原始测量值。可以看出源于目标的测量值完全淹没于杂波中。

基于EVT理论，用8 000个杂波样本数据离线估计状态回溯阈值。图3(a)给出了单帧杂波幅值极大值概率分布函数，以及估计的Gumbel概率密度函数。图3(b)给出了单帧杂波幅值最大值的积累分布函数，虚警率PFT=5%时对应的单帧回溯阈值为1.26。图3(c)给出了DP-SA方法在测量空间内对前20帧数据的幅值积累效果，可以看出所提方法能有效实现幅值积累。

表1统计了3种方法在不同杂波密度下的单次运行时间。可以看出，随着杂波密度增大，CPHD方法的运行耗时基本保持不变，而DP-SA方法与DP-TBD方法的运行耗时均略微增大，这是因为杂波密度增大时，Ψk+1(zk(i))内的候选状态数目随之增大，从而增加DP迭代步骤的计算量。相同杂波密度下，DP-SA方法的耗时与DP-TBD方法基本持平，较CPHD的运行耗时更少，能保证实时性。

表13种方法在不同杂波密度下的单次运行耗时

Table1Elapsedtimeofthreemethodsfordifferentclutterdensities

方 法单次运行耗时/sλ=1.0×10-2λ=3.0×10-2DP-TBD0.0520.183DP-SA0.0570.188CPHD0.2280.253

3.2 目标不存在

图6为目标不存在时20帧幅值积累值，图7给出了20帧累积的回溯阈值，以及最后时刻幅值的积累值。可以看出杂波幅值积累值低于回溯阈值，未发生误检。

4 结 论

本文针对强杂波背景下外辐射源位置不确定条件下的无源协同定位问题，提出一种基于DP-SA的APCL定位方法。所提方法对外辐射源位置不确定性鲁棒性更好，对目标位置估计更准确，且能保证实时性。在多目标场景下，尤其是多个目标航迹交叉时，所提算法会出现某个目标航迹跟丢的问题，这将是接下来的研究重点。