基于增广Burgers方程的音爆远场计算及应用

张绎典，黄江涛，高正红,*

1. 西北工业大学 航空学院，西安 710072 2. 中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

近年来，随着全球化经济的不断进步，人们对乘坐超声速客机进行长途旅行的渴望愈发强烈，各国也相继开展了不少有关超声速客机的研究项目。音爆噪声是制约早期超声速客机(如“协和”和图-144)持续运营的重要因素之一[1]，各国研究者对其关注的程度也日益增加。

音爆是超声速飞行器在近场产生的一系列以激波为主的扰动波，经过在大气层内的传播，最终在远场演化成的“N”形声波[2]。远场波形类似英文字母“N”的原因是声波在高温高压处的传播速度高于低温低压处，这种非线性传播效应造成了弱激波的堆积，最终在信号的两端形成两道较强的激波。准确的音爆预测是超声速飞机特别是超声速客机设计面临的重要技术问题。音爆模拟的关键是需要精确模拟音爆信号的过压值和上升时间[3]，它们和音爆强度直接相关。通过减小过压值，增加上升时间可以减弱音爆的强度。

目前的音爆预测方法主要分4类[4]：①基于Calson法的半经验预测方法[5];②基于超声速线化理论和声学的预测方法[6];③将计算流体力学(CFD)和声学结合的预测方法[7];④全场直接数值求解[8]。

方法①是半经验法，适用于工程估测。方法②和方法③都是先计算飞行器的近场声压，然后通过声学方法将预测声波传递至远场。二者的不同在于前者采用超声速线化理论计算近场而后者使用CFD的方法。由于线化小扰动理论仅适用于细长体，故方法③的适用面更广。方法④看似最简单直接，但因其巨大的计算量加上需要配套发展低耗散的高精度数值方法，国际上鲜有科学家进行尝试。2016年，东京大学的Yamashita和Suzuki[8]通过使用超算集群首次进行了音爆全场直接求解。但其模拟的海拔仅为500 m，远低于超声速客机的巡航高度(17 km左右)，同时一个模型的计算总时间达到了31.5 h。综上所述，统筹考虑计算量和计算精度，基于CFD和声学的预测方法是比较适合的方法，也是当代研究者主要关注的方法。

在得到近场过压分布后，通过声学的方法模拟远场声波信号也分以下3种方式来实现：①基于弱激波理论的波形参数法[9]；②基于时域、频域分析的Pestorius-Anderson法[10]；③基于非线性声学的增广Burgers方程法[7]。其中波形参数法只能模拟音爆的超压值，无法直接预测上升时间，也无法对结果进行快速傅里叶变换(FFT)得到感觉噪声级(Perceived Noise Level,PLdB)。过去，人们只能通过“3/p”定理[6]或稳态解理论(tanh方法)[11]等经验公式来估计上升时间的大小，这会影响音爆强度的预测精度，可能会导致飞机设计师做出错误的判断[7]。Pestorius-Anderson法需要在计算的过程中不断进行时频域变换，这样会造成误差的堆积，同时计算开销也随之增加。基于非线性声学的增广Burgers方程法直接在时域内对音爆传播过程进行模拟求解，排除了时、频域转换产生的误差，也减小了计算代价。同时，该方法可以考虑温度、湿度等环境条件对音爆传播的影响。因此增广Burgers方程类方法成为了学者较为关注的一类音爆远场预测方法。

近年来，音爆的相关研究也逐渐引起了国内学者的重视。朱自强和兰世隆[1]对音爆预测、优化方法做了详细梳理，指出了高精度流场模拟和增广Burgers方程等方法的优势。王刚等[12]对典型标模的音爆预测方法作了分析，指出采用适当几何修形和采用熵相容格式可以保证近场音爆预测精度。冯晓强等[13-14]发展了一整套基于CFD和波形参数法的音爆优化软件，并对低音爆机理进行了探究。但是，在音爆传播的模拟方法的选择上，国内学者几乎都采用了波形参数法等基于弱激波理论的方法，尚未看到通过增广Burgers方程来模拟音爆传播过程的研究。

本文主要就音爆远场计算展开研究。通过推导增广Burgers方程的无量纲形式，明确了其中各项的物理意义。采用算子分裂法，建立了增广Burgers方程的数值求解方法。接着，提出了一些方法来提高过压值、上升时间等音爆关键参数的计算精度。在此基础上，用自研的基于增广Burgers方程的远场传播程序计算了第二届国际音爆预测研讨会[15](SBPW-2)的两个标模(LM1021、Axibody)以验证程序的准确性。最后基于以上方法，研究了不同大气环境对地面音爆波形的影响，可为飞越不同气候环境的远程超声速客机的音爆预测提供参考。

1 Burgers方程理论

20世纪60年代，Blackstock[16]最早使用Burgers方程来模拟波在有损耗介质(Lossy Media)中的传播，提出了经典Burgers方程。在此基础上，他又和合作者Carlton[17]在70年代将经典Burgers方程扩展为广义Burgers方程(Generalized Burgers Equation)，使其能够模拟几何扩散(Geometrical Spreading)和非均匀介质对波传播的影响。1981年，Pierce[18]又将分子驰豫效应引入广义Burgers方程，并将其称作增广Burgers方程(Augmented Burgers Equation)。至此，该方程用以模拟音爆信号传播的形式基本固定。

1.1 经典Burgers方程

从Navier-Stokes方程可以得到忽略二阶以上小量的非线性波动方程——Westervelt方程[19]，其一维形式为

(1)

式中：p′为扰动声压；z为传播距离;t为传播时间;b和β分别为经典吸收系数和非线性系数;ρ0和c0分别为环境密度和环境波速，随海拔高度而变化。

为简化式(1)，引入坐标变换：

(2)

式中:t′为延迟时间，可以看做是波传播过程中某点的当地时间(即以波传播到当地的时间为时间原点)。

由链式法则可以得到式(1)中的各阶导数为

(3)

忽略二阶以上小量，经过化简后得到经典Burgers方程[18]为

(4)

这里值得注意的是，经过坐标变换后，耗散项为声压对延迟时间的二阶导，这和一般形式的Burgers方程中耗散项为声压对空间的二阶导有所区别。

1.2 增广Burgers方程的无量纲形式

在经典Burgers方程中加入非均匀介质、几何扩散以及分子驰豫效应的影响，即可得到增广Burgers方程[11]为

(5)

式中:S为声管面积[20];(Δc)ν为分子驰豫效应造成的声速变化量；τν为驰豫时间，下标ν表示不同的大气组成成分(如氧气、氮气)的驰豫过程。式(5)等号右边5项分别对应：非线性效应、经典吸收、大气分层、几何扩散以及分子驰豫效应对音爆的影响。

从增广Burgers方程的组成可以看出，该方程可以模拟声波在分层、有损耗的真实大气中的传播。

为了便于求解，首先对式(5)进行无量纲化处理：

(6)

增广Burgers方程的数值解法在附录A中给出。

2 算例验证

基于附录A中的的数值方法，开发了自研软件来进行远场预测，软件的框架如图 1所示。针对研发的过程中遇到的一些问题，提出了一些方法来提高过压值和上升时间的计算精度。使用SBPW-2的两个标准算例LM1021和Axibody来对软件进行校核。

2.1 验证算例简介

本文采用了音爆预测研讨会会议提供的两个标准算例来校核软件。该会议是美国AIAA学会组织的专门研讨音爆预测方法以及可信度校核的会议，至今召开两届(2014[21]年、2017[15,22]年)。该算例提供了完整的飞行数据、近场数据以及大气数据，可以准确设置增广Burgers方程的各项输入参数。由于该会议的影响力和权威性，国际上的学者广泛采用会议提供的标准算例来检验自己的音爆预测工具。

2.2 “缓冲信号”对上升时间的影响

以SBPW-2中的LM1021算例为例，选取周向角φ为0°的音爆信号为近场输入，周向角的定义如图 2所示。官方给出的近场输入信号如图 3中的黑色点划线所示。首先，直接使用官方给出的风洞试验数据作为近场输入进行了计算，并和NASA的sBOOM[23]软件的计算结果作了比较。如图 4所示，发现计算得到的远场信号的首段上升时间会偏小。导致这一现象的原因主要如下：增广Burgers方程中存在强非线性，初始波形中幅值不同的位置传播速度不同，幅值越大的部分传播速度越快。这一速度差就会导致时域中幅值为正的部分波形向左偏移，幅值为负的部分波形向右偏移。如果仅仅将计算域限制在有扰动的区域，最前端的正值信号就没有向左偏移的空间，这就导致了信号的失真。极端情况下会导致远场信号的首个上升段和纵轴重合从而无法正确预测上升时间。

为了验证上述原因，在官方给出的近场输入前加入一段无幅值的“缓冲信号”(如图 3所示)，就可以有效提升上升时间的模拟精度。图 4同时也给出了加入了“缓冲信号”后的远场输出。可以发现在加入“缓冲信号”后，远场输出的首个上升段基本和sBOOM的结果重合。由于非线性扭转的作用，前端信号又向前位移了一小段距离，约为0.005 s。换个角度来说，如果不加入“缓冲信号”，就相当于限制了音爆信号的总长度，在传播的过程中信号实际长度始终不变，从物理上来说也是不合理的。这种不合理的现象在近几年的一些期刊论文[7]中较为常见。

2.3 网格收敛性研究

同样以LM1021算例为例，选取收敛历程较有代表性的周向角为30°的音爆信号作为近场输入进行网格收敛性研究。

增广Burgers方程在时间和空间上各有一个维度，在这两个维度上的网格都是均匀的。下面依次对这两个维度进行网格收敛性分析：首先固定空间网格密度，对时间网格进行收敛性分析，然后固定时间网格密度，对空间网格进行收敛性分析。表 1和表 2分别给出了时间网格收敛性以及空间网格收敛性研究中的网格量和计算时间。其中：numz为空间网格的网格点数目：numt为时间网格的网格点数目。通常，人们更喜欢使用时间采样率(kHz)来表示时间方向的网格密度。

图5和图6分别给出了远场信号在时间和空间上的收敛历程。从中可以发现，远场波形对时间网格的密度更加敏感。加密时间网格后，远场波形的形态发生了较大的变化。需要将网格密度加密到一定程度后，得到的远场声压波形才逐渐收敛。相反，在空间方向加密网格后，地面波形并没有出现很大的变化。在SBPW-2[15]会议中，P4和P10这两位参会者可能因为时间方向的网格加密不充分，提交的结果出现了和低采样率的波形形态相类似的失真现象，如图 5所示。

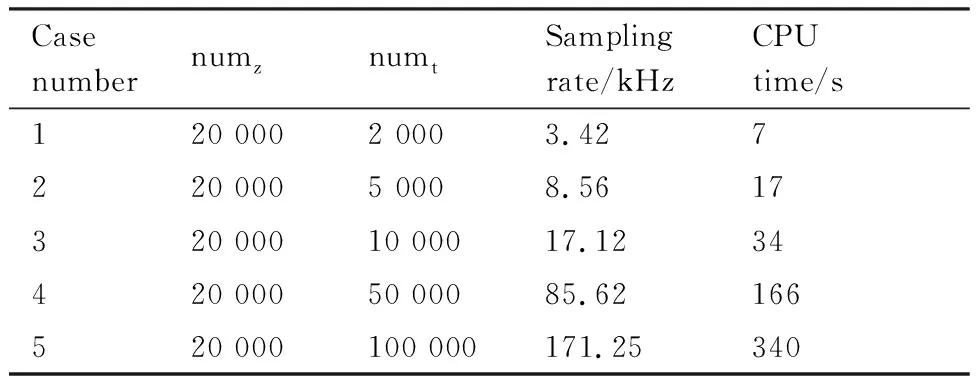
表1 时间网格收敛性分析算例Table 1 Cases for temporal mesh convergence study

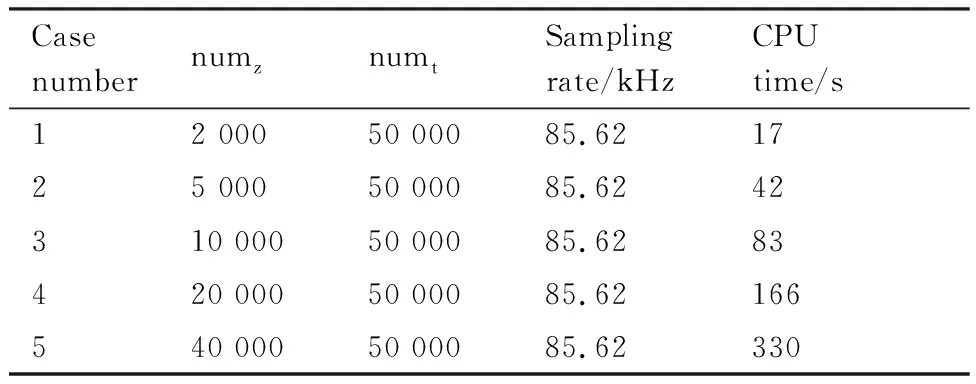
表2 空间网格收敛性分析算例Table 2 Cases for spatial mesh convergence study

综上所述，在运用上述的数值方法求解增广Burgers方程时，建议适当加密计算网格，尤其是时间方向的网格，建议的信号采样率为85 kHz以上。

2.4 LM1021算例验证

LM1021为SBPW-2的第一个标准算例，这是洛克西德·马丁公司设计的一款未来超声速客机，其几何外形如图 7所示，风洞测得的近场过压值分布(φ=0°,30° )如图 8所示。采用的大气参数为SBPW官方给出的标准大气，空气相对湿度为70%。

图9分别给出了自研程序和sBOOM在不同周向角下计算得到的地面波形。可以发现，二者预测的地面波形外形相似。当周向角为0°时(即飞机的正下方)，二者的计算结果基本重合。当周向角为30°时，二者地面波形的最后一个上升段斜率稍有偏差。

2.5 Axibody算例验证

Axibody为SBPW-2的第2个标准算例，其几何外形就是一个简单的几何回转体，如图 10所示。风洞测得的近场过压值分布如图 11所示，因为其对称特性，各个周向角测得的近场过压分布完全一致。采用的大气参数和前一算例一致。

图12分别给出了自研程序和sBOOM在不同周向角下计算得到的地面波形。可以发现，和LM1021算例的结果类似，二者的音爆预测结果达到了基本相当的精度。

3 增广Burgers方程在音爆模拟中的应用

基于上述自研程序，首先研究了经典吸收和分子驰豫效应这两种大气声吸收[24]效应对地面波形的影响，接着通过改变大气参数，分别模拟了超声速客机在大气层中飞行可能遇到的干燥、湿润、高温以及低温的大气环境，研究并比较了湿度和温度对于地面波形的影响。

3.1 大气声吸收对地面波形的影响

增广Burgers方程将经典吸收和分子驰豫效应这两种大气声吸收效应纳入考虑。理论[25]和试验[26]均证实，在低于10 MHz的频率下，经典吸收和分子驰豫效应是可以叠加的，因此在数值模拟中可以对其进行解耦。经典吸收是指声能因大气的黏性和导热性所造成的损失，而分子驰豫效应是因部分声能从声波的集总运动转移到分子内自由度中(转动和振动)而造成的[24]。这两种效应都导致了声波能量在传播的过程中被耗散为内能。

图13给出了分别使用增广Burgers方程法和波形参数法计算上文提到的LM1021这一算例的结果，周向角取0°。可以发现，由于考虑了传播过程中的损失，所以通过增广Burgers方程计算得到的远场信号中的压缩波是有厚度的，可以直接得到音爆的上升时间。而传统的波形参数法并不考虑声能在传播过程中因耗散而造成的损失，计算得到的地面波形是自然界中并不存在的无厚度的压缩波，需要通过一些经验公式来估计上升时间。这是增广Burgers方程类方法与波形参数法等线化理论方法最大的不同。另外由于耗散的原因，增广Burgers方程计算得到的过压值的峰值较低。综上所述，考虑了传播介质中的损耗的基于增广Burgers方程的模拟方法能够更真实地反映声爆在大气层中传播的物理过程。

图13还比较了经典吸收和分子驰豫效应各自对地面波形的影响。可以发现，如果在增广Burgers方程中仅考虑大气经典吸收效应的影响，最终得到的波形和不考虑大气声吸收的波形参数法的结果比较接近，波形的压缩波厚度并不明显。如果仅考虑分子驰豫效应的影响，相比于仅考虑大气经典吸收的情况，压缩波的厚度明显增加，并且最终的波形与增广Burgers方程的结果已经非常接近。基于以上的结果可以得出结论：分子驰豫效应对于音爆信号的耗散更为强烈。

3.2 湿度对地面波形的影响

未来超声速客机力求做到能在大陆上空超声速飞行，沿海和内陆的大气湿度相差很大，而湿度和分子驰豫效应的强度相关，所以有必要研究湿度对地面波形的影响。

为了简化研究，从近场到地面的大气相对湿度取一常数，选取了3个相对湿度(10%、50%、90%)来进行计算，其中10%的相对湿度模拟了沙漠、戈壁等干旱地区的湿度，90%的相对湿度则接近雨林、沿海等湿润地区的最高湿度。在研究的过程中固定温度、气压分布为标准大气分布。

图14给出了音爆信号在上述3种相对湿度的大气中传播得到的地面波形。总体来说，湿度对于波形幅值的影响不大。相对而言，干燥的空气对于声波的耗散更强，地面信号的过压值峰值更低。在起耗散作用的经典吸收和分子驰豫效应中,湿度的降低仅仅会使分子振动驰豫效应增强，而不会改变经典吸收的强度，因此总的声吸收强度会增强。

3.3 温度对地面波形的影响

基于和3.2节相同的原因，对温度对地面波形的影响作了研究。

以SBPW-2官方标准大气的温度分布为基准，分别给所有海拔处的温度增加15 ℃，使地面温度为40 ℃以模拟高温地区的温度。再给所有海拔处的温度相对标准大气减少15 ℃，使地面温度为-10 ℃以模拟低温地区的温度。在研究的过程中固定相对湿度(70%)、标准大气分布等环境参数。

图15给出了音爆在上述高温、低温以及标准的大气中传播得到的地面波形。总体来说，温度对地面波形的影响比湿度更加明显。相对而言，低温大气对声波的耗散更强，传播得到的最大过压值最低。在70%的相对湿度下，考虑起耗散作用的经典吸收和分子驰豫效应，温度的降低虽然会导致经典吸收效应减弱，但是低温亦导致了分子振动驰豫效应的增强，且因其增加的耗散比因经典吸收效应减弱而减少的耗散要多，这两种效应的叠加最终使总耗散增强。同时可以发现：低温的大气增强了传播中的非线性效应，这将导致上升时间的减小。

4 结 论

1) 相比于波形参数法等线化理论方法，增广Burgers方程类方法可以更准确地模拟音爆信号在真实大气中传播的各个物理过程，能够有效提高上升时间的模拟精度。

2) 在近场声压信号前加入一段无幅值的“缓冲信号”可以有效提升地面波形上升时间的模拟精度。

3) 基于算子分解法的增广Burgers方程的数值方法对于时间方向的网格数量更敏感，需要对其进行适当加密，建议的时间采样率为85 kHz以上，否则可能导致波形的失真。

4) 在经典吸收和分子驰豫效应这两种大气环境造成的声吸收机制中，分子驰豫效应对声能的损耗更大。

5) 干燥、低温的大气对地面音爆信号的过压值有抑制作用，但低温大气会减少音爆信号的上升时间。

在本文工作的基础上，未来拟开展结合音爆、气动的多学科优化设计[27]及考虑不确定因素的稳健设计[28-29]。