自适应设计空间扩展的高效代理模型气动优化设计方法

王超，高正红,*，张伟，夏露，黄江涛

1. 西北工业大学 航空学院，西安 710072 2. 中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

基于代理模型的优化(Surrogate-Based Optimization，SBO)方法可以提高优化设计效率，便于实现全局优化搜索，因此在工程设计领域得到广泛应用[1-4]。对于确定的优化问题，代理模型利用设计空间中有限的样本，通过一定的模型假设构建设计变量与目标函数的近似关系，并对设计空间中的未知点进行预测。代理模型的预测精度是影响基于代理模型优化效果的关键，工程设计中常采用具有描述强非线性问题能力的代理模型，如径向基函数(RBF)[5]、Kriging[6]、支持向量回归(SVR)[7]等模型，这类代理模型的预测精度与设计空间内样本的密度密切相关[8]。对于工程优化设计问题，特别是在初步设计阶段，通常需要选择尽可能大的设计空间，以获得具有全局最优的设计结果。然而，设计空间的扩大将直接导致样本在空间中的分布密度急剧下降，严重影响代理模型的精度。增加样本数目可以改善代理模型的精度，但是由此会带来巨大的计算代价，从而大幅度降低代理模型的优化效率。因此，如何构建尽可能包含全局最优设计点的有效设计空间，以及如何选择用于重构代理模型的有效样本是基于代理模型优化方法需要解决的关键问题。

Jones等[9]于1998年提出了基于Kriging模型的高效全局优化(Efficient Global Optimization，EGO)方法。EGO方法将优化搜索与代理模型加点重构相结合，根据Kriging模型对目标函数预测的均值和方差，将目标函数改善的期望(Expected Improvement，EI)作为Kriging模型优化的适应值函数。由于EGO方法同时考虑了代理模型的预测值以及预测的不确定性，因此具有全局优化能力[10]。Jones[11]对Kriging模型不同的加点函数进行对比研究时指出，EI加点准则存在收敛缓慢，优化效率低的问题。为了进一步提高EGO方法的全局性和高效性，Schonlau和Welch[12]将EI函数进行了推广，引入了一个调节算法全局和局部搜索能力的参数；Sasena[13]、韩忠华[14-15]等讨论了不同的加点函数和约束处理方法；Soberster[16]、Ginsbourger[17-18]、Liu[19]等发展了多种并行加点策略。

尽管各类改进的EGO方法提高了样本的利用率，但是对于大设计空间内的优化问题，EGO方法仍然难以实现全局性与高效性的统一。例如，对于气动外形优化设计问题，尤其是机翼/翼型等自由曲线曲面类的外形设计，如果增大设计空间，优化过程中会生成许多流场分离甚至无法计算收敛的“非翼型”外形，给样本带来许多“噪声”；另一方面，大的设计空间会导致代理模型的精度急剧下降[20]，代理优化需要大量的加点和更新，从而导致无法在可接受的计算代价内获得理想的设计结果。因此，应用EGO方法进行气动优化设计时，为了获得全局最优解，一般采用多轮优化的策略，即以上一轮优化的结果作为新的初始外形，重新划定设计空间进行优化。例如，Zhang等[21]对NACA0012翼型进行三轮优化，达到了全局优化的目的。但是，多轮优化的方法会导致人工成本增加，优化效率降低。

针对EGO方法在气动优化设计中面临的主要问题，本文对基于Kriging代理模型优化的加点方法和设计空间的构建问题进行了研究。首先，针对EGO方法本身的收敛性问题，本文采用先全局再局部的优化思想，提出了一种混合加点方法，该方法通过引入EI阈值控制不同的加点准则，以提高EGO方法在确定设计空间内的收敛性。针对设计空间的构建问题，本文对比了扩大设计变量范围和多轮优化两种不同的设计空间构建方法，分析了设计变量范围对设计空间大小和样本密度的影响，进而提出了自适应设计空间扩展的高效代理模型优化方法。自适应设计空间扩展的方法在动态的设计空间中进行优化搜索，只在有潜力的维度扩展设计空间边界，通过构建自适应的设计空间高效地分配样本。最后，通过AIAA气动优化设计讨论组(Aerodynamic Design Optimization Discussion Group，ADDG)[22]发布的标准翼型气动优化设计算例对本文提出的自适应设计空间扩展的优化方法进行了验证。

1 基于Kriging模型的混合加点方法

1.1 Kriging模型

Kriging模型是一种基于统计理论的插值技术，对于一定数目的样本集X=[x1x2…xn]T及其响应值y=[y1y2…yn]T，Kriging模型假设目标函数值与设计变量之间的真实关系可以表示为

y(x)=g(x)+z(x)

(1)

g(x)是回归部分，是用来描述全局趋势的函数，一般由多项式线性叠加表示，即

(2)

式中：fi(x)为低阶多项式基函数，可为0阶、一阶或二阶多项式；p为多项式基函数个数；βi为多项式回归系数，一般通过广义最小二乘法求得。

z(x)是一个静态的随机过程，用来描述真实样本与趋势函数之间的偏差，满足：

(3)

(4)

(5)

Kriging模型在未知点xnew的预测值表示为已知训练样本的线性组合，即

(6)

式中：c为线性加权系数。通过预测方差最小的无偏估计[23]方法，可以求得Kriging模型的预测值为

R-1(y-f(xnew)Tβ)

(7)

同时得到Kriging模型的预测方差为

σ2(xnew)=σz2[1+ζT(FTR-1F)-1ζ-rTR-1r]

(8)

式中：ζ=FTR-1r-f,F=[f(x1)f(x2)…f(xn)]T，R为样本点之间的相关函数R(xi,xj)组成的相关矩阵，r为未知点xnew与样本点之间的相关函数R(xnew,xi)组成的相关矩阵。

基于随机过程的Kriging模型与其他代理模型最大的区别是它的输出是一个随机变量，可以同时给出预测的均值和方差。根据Kriging模型预测的均值和方差，通过一定的加点准则[11]可以实现高效的优化设计。

1.2 EGO方法

基于Kriging模型优化最常用的是EGO方法[24-27]，又称EI加点准则。考虑以下一般性优化问题：

(9)

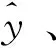
(10)

假设当前样本中目标函数的最小值为ymin，则Kriging模型在未知点处的预测值y相对于ymin的改善值为

I(x)=max(ymin-y,0)

(11)

根据Kriging模型对未知点预测的概率分布，可以计算任意未知点相对于当前最优值改善的期望。图1给出了目标函数改善的几何意义，图中红色部分为目标函数改善的概率，它反映了目标函数改善可能性大小。对目标改善值I(x)

求一阶矩，可以得到目标改善期望的函数为

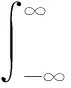
(12)

式中：Φ为标准正态分布函数；φ为标准正态分布的密度函数。

综上，对于式(9)中的原始优化问题，EGO方法的优化模型为

(13)

EGO方法将EI函数作为Kriging模型优化的适应值函数，每次把搜索到EI函数的最大值点加入到样本中，更新代理模型，直到满足终止条件。由于EGO方法可以同时考虑Kriging模型的预测值及其不确定性，因此具有高效的全局优化能力[9]。

用二维Rastrigin函数对EGO方法进行测试， 其函数表达式为

f(x,y)=x2+y2-10cos(2πx)-

10cos(2πy)+20

(14)

图2给出了二维Rastrigin函数图，该函数在x,y∈[-1,1]的设计空间内，存在多个局部最优，其中全局最优值为f(0,0)=0。

采用拉丁超立方取样(Latin Hypercubic Sampling, LHS)方法[28]生成20个样本，构建初始Kriging模型，然后采用EGO方法对Kriging模型进行优化，优化算法采用粒子群算法[29]，加点50次。图3给出了目标函数fmin的收敛历程，图4给出了每次搜索到EI函数最大值EImax的收敛历程。可见，在优化后期，EI函数的最大值变得非常小，其量级已经远小于目标函数的最小值(如图5所示)，此时EI函数已经无法对代理优化进行有效地指引。图6给出了初始样本和加点样本的位置，虽然EGO方法搜索到了最优区域，但是由于EI函数逐渐失效的问题，导致EGO方法在优化的后期基本变为随机搜索，优化收敛十分缓慢。

1.3 混合加点方法

针对EGO方法中EI函数在加点后期失效的问题，本文提出混合(Hybrid)加点方法：当EI函数的最大值小于设定的阈值CEI时，转换为最小预测值(Minimum Prediction, MP)加点准则。MP加点准则直接将代理模型对目标函数的预测值作为适应值函数，具有很强的局部挖掘能力，收敛速度快[11]，因此可以弥补EI函数失效的问题。本文构建的Hybrid加点方法的适应值函数表示为

Fitness=

(15)

式中：CEI=0.01ymin，即当前样本中目标函数最小值改善的期望小于1%时，由EI加点准则转换为MP加点准则。

使用Hybrid加点方法对二维Rastrigin函数重新进行优化，图7给出了加点过程中最大EI值与最小目标值的比值，可见当加到第34个点时，EImax/ymin<0.01，此时EI准则转换为MP准则。

图8给出了Hybrid加点过程中不同适应值函数搜索到的最优值，其中左轴代表EI函数最大值，右轴代表预测目标函数的最小值。

图9给出了Hybrid加点方法与EGO方法中目标函数的收敛历程对比，可见Hybrid方法明显优于EGO方法，EI准则向MP准则的转换大幅度加速了收敛进程。图10给出了Hybrid方法的加点位置，可见Hybrid方法首先采用EI准则，对设计空间的最优区域进行全局探索，当EI函数最大值小于CEI时，说明Kriging模型在设计空间最优区域内已经具有较高预测精度，此时转换为MP准则。由图10可见，Hybrid方法中的MP样本点均在全局最优值附近，可以对代理模型进行局部精细化挖掘，提高优化的收敛速度。

2 基于混合加点方法的翼型优化设计

分别采用EGO方法和Hybrid加点方法对RAE2822翼型进行气动优化设计。该算例为 ADODG[22]发布的第2个标准算例：跨声速黏性条件下RAE2822翼型减阻优化设计。翼型的设计状态为：马赫数Ma=0.734, 升力系数CL=0.824,雷诺数Re=6.5×105，优化目标为固定升力系数下阻力系数CD最小，约束条件为低头力矩系数Cm≤0.92，同时翼型的面积A不减小。RAE2822翼型优化的数学模型为

(16)

采用C型多块结构网格进行CFD计算，RAE2822翼型网格的拓扑结构如图11所示，c为翼型弦长，网格的具体参数如表1所示。

采用CST方法[30]对翼型进行参数化，翼型上下表面各12个设计变量，设计变量数目为24，给定每个设计变量的扰动范围，翼型的设计空间如图12所示。

使用LHS方法在设计空间生成100个初始样本，分别采用EGO和Hybrid方法添加200个样本点，在Hybrid方法中，设定CEI=0.01CD_min，CD_min为样本中的最小阻力系数。采用粒子群算法进行代理模型优化搜索，图13给出了不同优化

Table1ParametersofcomputationalgridofRAE2822airfoil

参数数值远场大小50网格规模601×213物面第一层网格距离5×10-6物面法向网格增长率1.13翼型前缘网格距离0.001翼型后缘网格距离0.001

方法中翼型阻力系数的收敛历程，表2给出了不同方法优化的翼型与初始翼型的计算结果对比，可见Hybrid加点方法的设计结果优于EGO方法，在满足约束的条件下，Hybrid方法优化翼型的阻力系数比RAE2822翼型降低了91.8 counts。

图14给出了使用Hybrid方法优化翼型与RAE2822翼型的外形对比，优化翼型头部变尖，最大厚度位置后移，后缘弯度增大。图15给出了优化翼型与RAE2822翼型的压力系数Cp分布对比，图16和图17分别给出了优化前后翼型流场的压力云图。可见，优化翼型的前缘吸力峰增大，后加载增加，压力恢复平缓，激波得到消除。

Table2OptimizationresultsofEGOmethodandHybridinfillmethod

方法CLCDCmARAE28220.8240.020 31-0.092 70.077 9EGO0.8240.011 25-0.091 90.077 9混合加点方法0.8240.011 13-0.091 90.077 9

3 设计空间的扩展

3.1 代理模型加点分析

为了进一步探讨设计空间对优化结果的影响，首先对RAE2822翼型优化算例中的设计变量进行归一化处理。图18通过平行坐标系显示了Hybrid方法中设计空间各维度的边界以及在优化过程中所有的加点样本，图19给出了所有加点样本对应的翼型外形。统计发现，加点样本中有98.5%的样本的某一维(或多维)落在设计空间的边界，其中最优样本也位于设计空间的边界处。由此可见，第2节RAE2822翼型优化算例中的设计空间不足以寻找全局最优，因此需要对翼型的设计空间进行扩展。

3.2 扩展设计空间

设计空间的构建和样本的选取是基于代理模型优化的关键，为了分析不同的设计空间扩展方法和样本数目对设计结果的影响，本文对比以下两种设计空间扩展方法：

方法1直接扩展空间。将原始设计空间每一维的变化范围扩大一倍，扩展的翼型设计空间如图20所示。该方法中，初始样本数目为100，加点500次，样本总数为原始空间优化的2倍。

方法2两轮优化。以原始设计空间优化的翼型为初始，进行第2轮优化，每一维设计变量的变化范围与第1轮优化保持一致，第2轮优化翼型的设计空间如图21所示。该方法中，初始样本数目为100，加点200次，第2轮优化使用的样本总数与原始空间优化相同。

使用Opt1代表方法1的优化结果，Opt2代表方法2的优化结果，两种方法优化阻力系数的收敛对比如图22所示，优化的翼型外形以及压力分布对比如图23和图24所示。可见，直接扩展空间优化的翼型与原始空间优化的翼型差异很大，翼型上表面仍然存在明显的激波。表3给出了两种设计空间扩展方法优化翼型的计算结果对比，可以发现，直接扩展空间的方法不如原始空间的设计结果，而第2轮优化的结果优于原始空间的设计结果。图25给出了第2轮优化中的加点样本与设计空间边界，可见最优样本落在设计空间内部， 即第2轮优化的设计空间包含了最优点。

该算例表明，设计空间的构建方法对代理模型优化设计结果有重要的影响，在相同的计算成本下，直接扩大设计空间的方法不如多轮优化的方法。

方法CFD调用次数CDCmA初始翼型0.020 31-0.092 70.077 9原始空间优化3000.011 13-0.091 90.077 9第2轮优化3000.011 06-0.091 80.077 9直接扩展空间6000.011 54-0.091 10.077 9

为了进一步分析设计变量范围对设计空间的影响，假设每一维设计变量的变化范围均为R，维数为D，则设计空间的大小可以用空间的超体积表示为

V=RD

(17)

设计空间超体积随着变量范围的变化率为

(18)

可见，设计空间的大小随变量范围呈D-1次多项式增长。对于RAE2822翼型优化算例，如果每一维设计变量的范围增加一倍，则设计空间扩大为原来的224倍。

Kriging模型的精度与设计空间样本的密度密切相关[20]，直接扩大设计变量范围会导致设计空间的暴增，从而带来样本严重的稀疏性，代理模型的精度大幅下降，如图26所示。因此，如果直接扩展设计空间，代理优化难以收敛，无法在可接受的计算代价内获得理想的设计结果。

在两轮优化的方法中，以第1轮优化的结果为初始外形，划定与第1轮优化同样的变量范围，则搜索空间只增加了一倍，所以第2轮优化采用同样的样本得到了理想的设计结果。因此，在实际的翼型设计中，切实可行的方案是进行多轮优化而不是一次性给定足够大的变量范围。

4 自适应设计空间扩展方法

在基于代理模型的气动优化设计方法中，设计者一般难以直接构建合理的设计空间，如果设计空间太大，将导致有限的样本难以满足代理模型的精度要求，从而无法获得理想的设计结果；如果设计空间太小，则需要多轮优化，但是多轮优化不仅增加了人工成本，而且降低了设计效率。针对代理模型气动优化中设计空间的构建问题，本文提出自适应设计空间扩展的优化方法，该方法不再固定设计空间的大小，设计空间在优化过程中进行动态变化，只在有潜力的维度自适应扩展设计变量范围，通过构建自适应的设计空间，提高样本的利用效率。

在RAE2822翼型优化算例中，加点样本大部分都落到设计空间的边界上，主要有两方面的原因：一方面是因为设计空间太小，最优解在设计空间之外，导致优化搜索到了边界；另一方面是因为代理模型在边界处的精度太差，导致优化搜索到了错误的最优。基于上述两点原因，在进行设计空间扩展时，需要同时满足边界要求和精度要求。本文构建的自适应设计空间扩展的代理模型气动优化框架如图27所示，具体步骤为

Step1设定初始的设计空间，即设计变量的个数以及每个设计变量的变化范围。

Step2利用LHS方法在设计空间选取初始样本，将初始样本添加到样本库。

Step3根据样本库确定设计空间的边界Xmin和Xmax，构建当前的设计空间。其中Xmin为样本库中每一维的最小值组成的向量，Xmax为样本库中每一维的最大值组成的向量。

Step4利用样本库中的样本构建代理模型。为了提高优化效率，每添加10个样本，重新训练Kriging模型的超参数。

Step5根据代理模型的加点准则，优化搜索得到Xbest。

Step6CFD评估Xbest，并将Xbest加入到样本库。

Step7判断Xbest是否满足设计空间扩展条件。如果代理模型在Xbest处的预测值满足精度要求，并且Xbest的某些维到达当前设计空间的边界，则生成自适应样本点Xadaptive，CFD评估Xadaptive，并将Xadaptive添加到样本库。

Xadaptive由Xbest通过在某些维度扩展生成，其作用是扩大设计空间的边界。Xadaptive的计算方式为

(19)

式中：coefficient为设计空间扩展系数，本文取0.1。

Step8判断样本总数N是否达到设定的最大样本数目Nmax，如果N>Nmax，则终止程序，否则转到Step 3。

采用本文构建的自适应设计空间扩展的优化方法对RAE2822翼型重新进行优化设计，初始样本数为100，加点200次。以初始设计空间为参考对样本每一维设计变量进行归一化处理，图28给出了初始设计空间与最终设计空间中设计变量的边界对比，对应翼型外形边界如图29所示。由图可见，初始设计空间在某些维度进行了自适应地扩展。表4给出了不同方法的优化结果，自适应设计空间的优化结果与第2轮优化结果基本一致，该方法通过一次优化便达到了多轮优化的效果，因此大幅提高了气动优化的效率。

方法CFD调用次数CDCmA初始翼型0.020 31-0.092 70.077 9原始空间优化3000.011 13-0.091 90.077 9第2轮优化3000.011 06-0.091 80.077 9直接扩展空间6000.011 54-0.091 10.077 9自适应扩展空间3000.011 05-0.091 90.077 9

图30和图31分别给出了使用不同方法优化的翼型外形以及压力分布对比，可见优化的翼型外形以及压力分布十分相似，说明该算例的“最优”翼型集中在初始翼型附近的一个区域。

为了对RAE2822翼型优化结果的可靠性进行验证，将本文的优化结果与文献[21]中的结果进行对比，如表5所示。可以发现，由于网格和CFD求解器的不同，不同方法对初始翼型和优化翼型计算的气动力系数存在一定的差异，因此难以直接衡量优化结果的优劣。从翼型的外形与压力分布来看，文献[21]中优化翼型的外形以及压力分布的形态与本文的结果十分相似，二者均得到一个典型的跨声速无激波压力分布，如图32和图33所示。

与文献[21]中基于代理模型优化方法的计算代价进行对比，本文的CFD计算次数为300，文献[21]采用多轮优化的方式，CFD计算次数为592。由此可以看出，本文提出的自适应设计空间扩展方法的优化效率得到大幅提升。

表5 与文献[21]中RAE2822翼型的优化结果对比Table 5 Comparison with optimization results of RAE2822 airfoil in Ref. [21]

5 NACA0012翼型优化设计

为了进一步验证自适应设计空间扩展优化方法的适用性，本节对NACA0012翼型进行优化设计。该算例为ADODG[22]发布的第1个标准算例：跨声速无黏条件下NACA0012翼型的减阻设计。从文献[31-36]的结果可以看出，该算例的优化结果与初始翼型相比，变形尺度非常大，可以更好地考验自适应设计空间扩展方法的能力。

该算例的设计状态为：Ma=0.85，迎角α=0°，优化目标为0°迎角下翼型阻力系数最小，约束条件为翼型每个位置处的厚度t不减小。NACA0012翼型优化的数学模型为

(20)

由于该算例为0°迎角下对称翼型的优化，本文采用半模外形进行计算和优化，全模翼型的阻力为半模外形的2倍。采用O型多块结构网格进行CFD计算，初始翼型网格的拓扑结构如图34所示，网格参数的设置如表6所示。

采用CST方法对翼型进行参数化，设计变量数目为24，给定每个设计变量的扰动范围，翼型的初始设计空间如图35所示。

采用构建的自适应设计空间扩展的优化方法对NACA0012翼型进行优化，并与固定设计空间的优化方法进行对比。初始样本数目为100，加点200次。图36给出了归一化后初始设计空间与最终设计空间的边界对比，对应的翼型外形边界如图37所示，可见自适应设计空间的方法在翼型的后缘大幅度地扩展了设计变量的范围。

Table6ParametersofNACA0012airfoilcomputationalgrid

参数数值远场大小50网格规模201×201物面第1层网格距离5×10-4物面法向网格增长率1.05翼型前缘网格距离0.001翼型后缘网格距离0.001

图38给出了自适应设计空间与固定设计空间方法优化阻力系数的收敛历程，在相同的计算花费下，自适应设计空间的方法获得了更优的结果。表7给出了不同设计空间下翼型优化结果对比，自适应设计空间优化的翼型阻力系数为55 counts，明显小于固定设计空间的优化结果。

图39和图40分别给出了固定设计空间与自适应设计空间优化的翼型外形以及压力分布对比。可见，自适应设计空间优化的翼型前缘和后缘更加饱满， 翼型前缘半径增加，后缘变形尺度增大；从压力分布来看， 自适应设计空间优化的翼型前缘的吸力峰更高，翼型后缘通过连续地膨胀和压缩使压力得到缓和恢复，从而减弱了激波强度，降低了激波阻力。

方法CLCDNACA001200.047 1固定设计空间00.017 5自适应设计空间00.005 5

从总压损失的角度进一步分析优化翼型阻力系数减小的原因。在可压缩条件下，总压与静压的关系以及总压系数表示为

(21)

(22)

式中：p0为总压;p为静压;Ma为当地马赫数;γ为气体比热比;p∞为远场静压;ρ∞为远场密度;v∞为自由来流速度。

NACA0012翼型以及两种不同方法优化翼型的流场总压系数云图如图41～图43所示，截取翼型表面的总压系数如图44所示。由图可见，NACA0012翼型激波最强，在激波位置处总压下降最明显。图45给出了翼型后缘一倍弦长处(x/c=2)截面总压系数的对比，可以发现，该截面处自适应设计空间优化翼型的总压相对来流总压损失最小，即能量损失最小，因此该翼型的阻力系数最小。

将本文的优化结果与文献[21]中结果进行对比，图46和图47分别给出了文献[21]通过多轮优化方法得到的翼型外形和压力分布，该结果与本文的优化结果具有很强的一致性。表8给出了两种不同方法优化的结果对比，可以发现，本文的方法通过更少的CFD计算代价获得了阻力更小的翼型。

该算例进一步证实，自适应设计空间扩展优化方法对于大尺度变形的气动优化问题具有很好的适应性。

表8 与文献[21]中NACA0012翼型的优化结果对比

6 结 论

本文针对基于Kriging模型气动优化中的加点方法以及设计空间的构建问题进行了研究，提出了混合加点方法和自适应设计空间扩展的优化方法，通过ADODG[22]标准翼型优化算例对文中提出的方法进行了验证。

1) 文中构建的混合加点方法通过引入EI阈值控制EI和MP加点准则，利用先全局再局部的优化思想，可以提高EGO算法在确定设计空间内的收敛性。

2) 设计空间的构建方法对基于代理模型气动优化的结果有重要的影响，如果设计空间的尺度偏于保守，则搜索空间受到限制，从而失去全局优化能力；如果设计空间的尺度偏于激进，将导致有限的样本难以满足代理模型的精度要求，从而无法获得理想的设计结果。

3) 本文构建的自适应设计空间扩展的方法打破了传统代理模型优化依赖人工经验给定设计空间的局限，通过构建自适应的设计空间，实现了样本的高效配置，很好地兼顾了气动优化的高效性和全局性。通过ADODG标准翼型气动优化设计算例证实，自适应设计空间扩展方法可以大幅提高气动优化效率。