理解学生:教学的“最佳路径”
江苏南京市长江路小学(210018) 周 圆
小学语文教材中有一篇文章叫《最佳路径》,说的是世界著名建筑大师格罗培斯从事建筑研究多年,也留下很多杰作,个人成绩斐然,但是却为设计如何联结迪士尼乐园各景点之间的小路而大伤脑筋,无论怎么修改设计方案,都无法找到一条最佳路径。于是格罗培斯放弃所有的设计方案,在乐园的地面上撒上草种。没多久,小草长出来了,整个乐园被绿草所覆盖,在迪士尼乐园提前开放的半年里,草地被人们踩出许多小道,这些小道有宽有窄,优雅自然。第二年,格罗培斯让人按照这些踩出的痕迹铺设了人行道。这条被人们踩出来的路径在1971年伦敦国际园林建筑艺术研讨会上被评为“世界最佳路径”。
那么教学的“最佳路径”又是什么样的呢?显然,教学的“最佳路径”绝不是教师为学生“设计”出来的,无论教师多么有经验,多么优秀,“最佳路径”都应该让学生自己“踩”出来。教师只有基于对学生这种自由的、真实的“踩路”行为的理解,才能找到教学的“最佳路径”。
理解学生,是教学的基本原则,更是有效教学的前提条件。那么,在数学教学中,教师如何才能做到理解学生,从而找到教学的“最佳路径”呢?
一、理解学生数学学习的“出发点”,精准切入
学生在学习“7的乘法口诀”之前,已经学习了“1~4的乘法口诀”“5的乘法口诀”和“6的乘法口诀”。“1~4的乘法口诀”是学生初次接触乘法口诀,重点应落在对乘法口诀意义的理解;“5的乘法口诀”则是以5的乘法口诀为例,系统呈现乘法口诀的编排规律;“6的乘法口诀”再次强化乘法口诀的编排规律。
学生在学习了“1~6的乘法口诀”的基础上,不但理解了乘法口诀的意义,也掌握了乘法口诀的编排规律,多次经历了“情境导入——加法计算——乘法算式——乘法口诀”的过程。那么作为“表内乘法”第二单元开篇的“7的乘法口诀”,还要沿袭这种模式去教学吗?
为了摸清学生的真实学习起点,课前我对两个班共80名学生做了学情调查,发现学生不但对编制口诀的过程了如指掌,而且大多都能背出7的乘法口诀。
面对这样的学情(如图1所示),对于这么高的学习起点,怎能还按部就班地重复同一个学习模式呢?于是我打算这样切入:发布前测情况,准确定位学生学习的出发点,调动学生学习的主动性。由于学生最不熟的就是“四七”的乘法口诀,所以我就让学生小组合作研究“当他们记不清‘四七’了,学生就有了学习的积极性,不再是机械重复地编制口诀的“四部曲”,而呈现了别样的精彩(如图1):有画图的,有转化成加法来推算的,还有根据口诀来推算的……
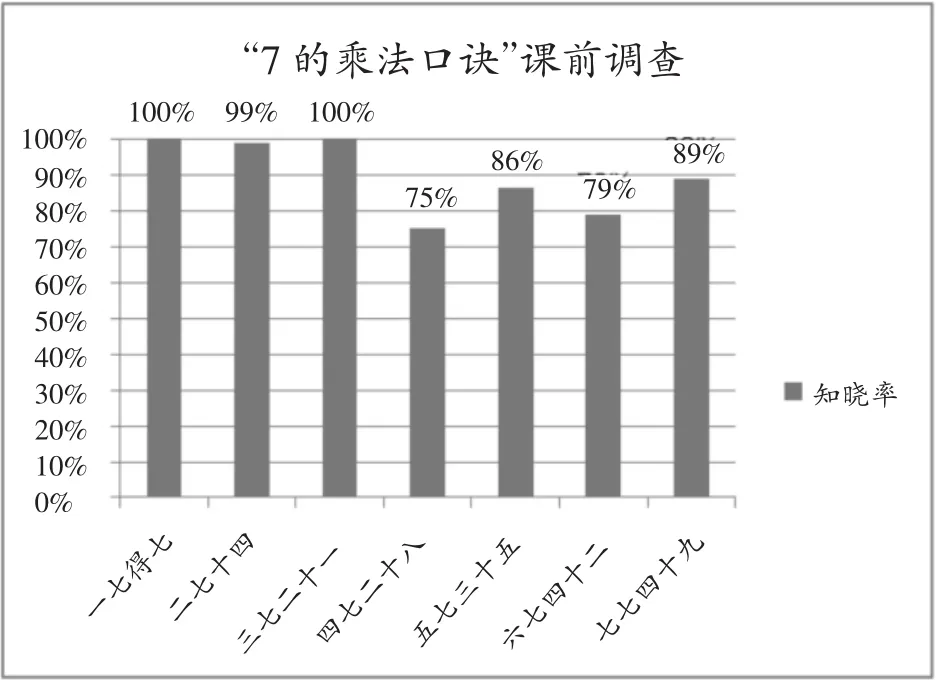
图1
画图的作品中,除了画圆圈、画三角形等外,还有画“糖葫芦串”的,特别是糖葫芦串画法得到了大家的一致好评,认为7个糖葫芦串成一串特别形象,很好地体现了“4个7相加”。
转化成加法的学生也有不同的想法,有的用“7+7+7+7=14+7+7=21+7=28”逐个累加,计算出4个7是28,还有的进行“7+7+7+7=14+14=28”的巧算,这种方法很好地体现了“乘法是相同加数相加的简便运算”这一本质。
有的学生是据自己熟悉的口诀来推算的,但也有不同的思路;有的学生根据前一句口诀“三七二十一”来推算,有的学生根据后一句口诀“五七三十五”来推算,还有的学生根据口诀“四六二十四”来推算。这些学生不但掌握了7的乘法口诀,还和同学分享了口诀之间的联系,尤其是根据“四六二十四”来推算“四七”的学生,他们能够主动构建立体的知识网络,懂得分析和推理,这种能力实在让人不得不点赞!
你给学生多大的舞台,学生就能给你多大的精彩!因为准确切入了学生数学学习的出发点,所以才闪现出了学生如此多的思维火花!
二、理解学生数学学习的“生长点”,巧妙衔接
“生长点”这一概念是由自然科学的含义引申而来的,泛指与某一事物联系较紧密的,由此事物生发出来的,有明显传承或依附关系的事物。数学学习的生长点,就是指与后续学习有明显传承或依附关系的核心基础知识。
例如,探究“三角形的内角和”时,很多学生采用先量再算的方法,但是因为测量有误差,有的学生得出的三角形内角和是181°或179°,对此,教师只能解释:“其实我们测量每个角的度数时是可能产生误差的,所以才导致得出的三角形的内角和不是正好等于180°,事实上三角形的内角和真的是180°。”但一些颇有“追根究底”精神的学生显然对这样的回答不满意,很快就有学生提出可以利用计算机精确测量、自动计算的功能进行科学验证。这种方法,不但可以解决测量误差的问题,而且在理论上可以把所有三角形都验证一遍。
如果教学止步于此,仅停留在利用计算机验证,而没有抓住学生数学学习的生长点就太可惜了。于是,我这样进行教学:紧跟着计算验证这第一个层次,增加了两个层次。第二个层次让学生找出三角形三个角的变化规律:当∠1逐渐变大时,∠2和∠3是怎么变化的;当∠1逐渐变小时,∠2和∠3又是怎么变化的。第三个层次是在前两个活动的基础上引导学生展开想象:随着三角形的高越来越长,∠1变得无限小,并无限趋向于0°,而∠2和∠3无限趋向90°,所以三角形的内角和是0°+90°+90°=180°;随着三角形的高越来越短,∠1 变得无限大,并无限趋向于180°,而∠2和∠3无限趋向0°,所以三角形的内角和是 180°+0°+0°=180°。
根据奥苏伯尔的有意义学习理论,学生认知结构中已有的适当知识对新知识的有意义学习起固着作用。量、算、验证,是学生原有水平就能轻松完成的空间知觉活动,学生能够找出三角形三个角的变化规律,感悟随着一个角的变化另外两个角是怎么变化的,从静态的单个三角形走向动态的、变化的多个三角形,建立三角形的形状、大小等相关空间表象,再基于对变化规律的认识引出极限思想,展开空间想象。从空间知觉水平到空间表象水平,再发展到空间想象水平,是建立空间观念非常重要的“三部曲”。对于同一个数学素材,如何才能巧妙衔接学生的原有认知和新纳认知?关键在于理解学生数学学习的生长点。
三、理解学生数学学习的“延伸点”,深入浅出
《义务教育数学课程标准(2011年版)》提出“要注重培养学生的应用意识”。所谓数学应用意识,是指应用数学知识、思想方法的自觉心理倾向性。它包含两个方面的含义,一方面是从数学到现实(具体化过程);另一方面是从现实到数学(数学化过程)。如果说有意识地利用数学的概念、原理和方法来解释、解决数学问题是学生数学学习的一个生长点,那么利用现实生活中的现象和问题来演绎数学模型、解释数学原理就是学生数学学习的延伸点。
例如,学生在自主探索“小数乘法”的过程中,出现很多错误(如图2)。
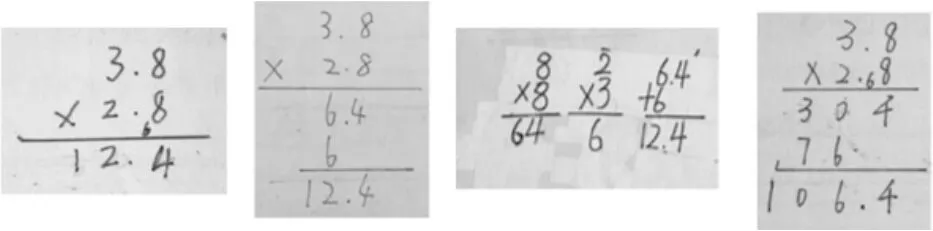
图2
怎样让学生心悦诚服地接受小数乘法的计算方法?并不是教师告诉学生“先按整数乘法的法则算出积,再看因数中一共有几位小数,就从得数的右边起数出几位,点上小数点”,然后学生按照教师给出的运算法则去机械模仿就行了。只有数形结合,用现实模型演绎出算理算法,“深入”探究小数乘法的运算规律,让其中的道理“浅出”,学生的学习才能达到不一样的境界。
因此,当教师给出图3后,学生恍然大悟——原来错在漏算了一部分的面积,正确算法的每一步计算过程分别对应图形中一块的面积:深色部分面积对应的是8分米×38分米,也就是0.8米×3.8米;浅色部分对应的是20分米×38分米,也就是2米×3.8米。这样学生就能知其然且知其所以然,同时对多位数乘法的法则、小数乘法与整数乘法的关系有深刻的感悟。
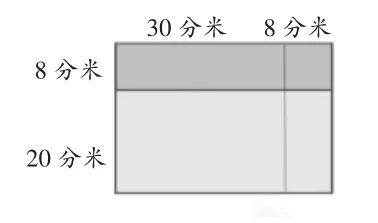
图3
四、理解学生数学学习的“兴趣点”,点燃激情
《义务教育数学课程标准(2011年版)》特别提到,课堂教学应激发学生兴趣,调动学生积极性,引发学生的数学思考。“兴趣好比路灯,引导你走向成功;兴趣好比船桨,带着你驶向远方;兴趣好比是一双羽翼,领着你翱翔天际。兴趣是最好的老师,它会引你走向光明。”如果不能抓住学生数学学习的兴趣点,学生会觉得数学枯燥乏味,就无法产生学习激情。
例如,若按照常规教学思路来教学“万以内数的大小比较”,则是“先比较几组数的大小,然后总结出比较大小的方法:先看数位,数位不同,数位越多,这个数就越大;数位相同,则从最高位依次往下比”。对此,学生是很容易掌握相关知识,但会觉得索然无味。黄爱华老师在教学时利用了游戏的形式,一下就激发了学生的学习兴趣。一共有三轮游戏,第一轮游戏的规则是“第一次抽到的数字就放在个位上,第二次抽到的数字放在十位上,第三次抽到的数字放在百位上……”限定了摆放次序,学生会在摸出下一张牌之前就积极动脑思考,想着摸出什么数字才能赢,殷切期盼着能赢的一类数字会出现,而不是只能遵从教师出示的数去比较某一个固定的数。第二轮游戏的规则改为“第一次抽到的数字放在千位上,第二次抽到的数字放在百位上,第三次抽到的数字放在十位上……”,虽然还是限定摆放次序,但是却从千位摆起(顺序反了),能引导学生在不知不觉中整理归纳比较数的大小的方法。第三轮游戏的规则更开放了,改为“每次抽到的数字由抽签者自己决定放在哪一位上”,这对学生来说真是一个不小的挑战,学生需要综合考虑各种因素,把在之前游戏中学到的本领都用上。越是有挑战性,学生越是想赢,越能挖掘自身的潜能,激情燃烧自己的脑细胞!这样的寓教于乐,学生不但学得有兴趣,思维更是得到了综合锻炼。
玛格利特·米德将社会文化划分为三种形态:前喻文化、同喻文化和后喻文化。前喻文化是通过自上而下的传递,即年幼者向年长者学习的文化;同喻文化是通过同辈互动传递,即同辈之间相互传授、相互学习的文化;后喻文化是通过自下而上传递,即年长者向年幼者学习的文化。当前,我国已经加速进入了后喻文化时代。在这种文化条件下,学生的很多想法都值得教师去思考和学习。只有理解学生,才能找到通向学生真实想法和心灵深处的路径,这便是教学的“最佳路径”!
--先进无机材料论坛例记(Ⅱ)
--先进无机材料论坛例记(Ⅰ)

