不同湍流模型下空中加油吊舱尾流场对比分析

，

(中国飞行试验研究院发动机所，陕西 西安 710089)

0 引言

在进行空中加油过程中，加油机的翼尖涡、加油机发动机尾喷流以及空中加油吊舱尾流场对受油机和加油机能否成功对接具有非常重要的影响，空中加油吊舱尾部的流场分布对于空中加油软管和锥管的安全回绕也具有很大影响。对于空中加油流场的数值模拟，国外文献参考文献[1]采用SST模型对飞机机翼翼尖涡和发动机尾喷流进行了数值模拟；文献[2]采用大涡模拟(LES)方法，计算了NACA2415后面的总压云图、温度云图、马赫数云图以及涡量图；文献[3-5]对加油软管和锥管的气动特性进行了数值模拟。国内对空中加油流场的数值模拟较少，文献[6]采用标准k-ε模型计算了两种受油管尾部的湍动能分布和噪声情况。本文中的计算区域为加油吊舱尾部至机身尾部的区域，选取典型高度和典型速度，分别采用RNGk-ε模型、标准k-ε模型和剪切应力传输SSTk-ω模型三种湍流模型。将三种湍流模型的计算结果进行对比分析，用空中加油飞行试验对计算结果进行验证。本文研究的内容对后续空中加油流场的仿真计算，空中加油飞行试验时对接—脱离过程中飞行员的操作、软管的拖曳—回绕包线确定、空中加油包线的确定具有指导意义，对后续空中加油吊舱尾部结构的优化设计也具有借鉴意义。

1 控制方程

流体的运动一般要遵循三个最基本的守恒定律，即质量守恒定律、动量守恒定律和能量守恒定律，在流体力学中具体体现为质量方程、动量方程和能量方程，它们是基本的控制方程。

1.1 质量方程

质量守恒方程简称质量方程，又称连续性方程，它的微分表达式为：

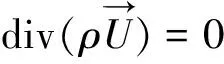
(1)

1.2 动量方程

动量守恒方程简称动量方程，又称运动方程，它实质上是牛顿第二定律，它的微分表达式为：

(2)

1.3 能量方程

能量守恒方程简称能量方程，它实质上是热力学第一定律，它的表达式为：

(3)

1.4 湍流模型

湍流模型是附加的控制方程，它的作用是和基本控制方程一起组成封闭的方程组来描述湍流运动，本文的湍流模型分别选用RNGk-ε模型、标准k-ω模型和剪切应力传输SSTk-ω模型，它们将分别和基本控制方程一起来描述湍流运动。

1.4.1 RNG k-ε模型

RNGk-ε模型(以下简称RNG模型)的基本思想是把湍流视为受随机力驱动的输运过程，通过频谱分析的方法消去其中的小尺度涡并将其影响归并到涡粘性中，以得到所需尺度上的输运过程。该模型与标准模型具有相同的模式，但是采用了重整化群方法，修正了湍流粘度，考虑了平均流动中的旋转及旋转流动情况，在ε方程中增加了一项，从而反应了主流的时均应变率，改善了精度，可以更好地处理高应变率及流线弯曲程度较大的流动。

湍动能k方程：

(4)

耗散率ε方程：

(5)

式中，总压生成项和标准模型一样。

该模型和标准模型的主要区别在于ε方程中的c1修正：

(6)

(7)

(8)

模型参数：c1=1.42，c2=1.68，cμ=0.0845，η0=4.377，β=0.012。

1.4.2 标准k-ω模型

标准k-ω模型(以下简称k-ω模型)的优点之一就是低雷诺数条件下的近壁处理，在模拟壁面边界层、自由剪切和低雷诺数流动时性能更好，可以用于模拟逆压梯度下的边界层分离，对于定常、不可压流动，k方程为：

(9)

ω方程为：

(10)

(11)

Pk为速度梯度引起的总压生成项：

(12)

模型参数：β′=0.09，α=5/9，β=0.075，σk=2。

1.4.3 剪切应力传输SSTk-ω模型

由于标准k-ω模型没有考虑湍流剪切力的影响，导致过高地估计了湍流粘度，因此在分离流的预测上产生一定的失真。在此基础上提出剪切应力传输SSTk-ω模型(以下简称SST模型)，通过限制湍流粘度，考虑湍流剪切应力的传播，在近壁自由流中有更广泛的精度和可信度。SST模型由于在壁面附近采用k-ω模型，在远区采用k-ε模型，因此对分离流有很好的预测效果，但由于对壁面距离的依赖使得它不适合于模拟自由剪切流动。

(13)

(14)

其中，Gk为湍动能，Gω为ω方程，Γk和Γω分别为k和ω的有效扩散项，Yk和Yω分别为k和ω的发散项，Dω为正交发散项。

2 模型简介

本文中的加油吊舱挂装在机腹下方，加油吊舱尾部至机身尾部的距离是8 m，加油吊舱位于加油机两台发动机中间，两台发动机舱之间的距离是2 m，加油吊舱尾部距离机腹表面0.1 m。建立如图1所示的某型空中加油吊舱尾部至机身尾部的计算域网格模型，整个计算域长10 m、宽2 m、高3 m，模拟加油吊舱挂装在机腹下方时加油吊舱尾部至机身尾部的流场分布情况。由于吊舱尾部的几何结构不规则，所以采用分块划分网格方法，将计算域划分为几个规则区域，分别划分六面体结构化网格，网格总数170万。计算域进口边界条件为速度入口，出口为自由流边界条件。

图1 计算域网格模型

3 仿真计算及结果分析

将网格文件导入Fluent软件，并对网格进行检查，通过检查项中的Domain Extents来判断所建立的流场是否符合要求，Minimun Volume确定是否出现负体积，如果出现负体积必须对网格重新划分，采用基于总压的耦合隐式算法。

分别选取上述三种湍流模型，计算了飞行高度Hp=6 km，飞行速度Vc=570 km/h，攻角θ=3°雷诺数Re=2.85×106条件下的流场分布情况。下文将详细给出三种湍流模型计算出的吊舱尾部后面不同截面上的总压分布情况、速度分布情况和涡量分布情况，并对计算结果进行对比分析。

3.1 总压分布图

对吊舱尾部后流场的分析，选取X=4(距离吊舱尾部2 m)和本文计算域出口X=out(距离吊舱尾部距离为8m)两个截面上的流场进行分析。图2为使用RNG湍流模型的计算结果，图3为k-ω湍流模型的计算结果，图4为SST湍流模型的计算结果。从图2中可以看出，随着距加油吊舱尾部后距离的增大，总压分布趋于均匀，也就是说气流分布趋于均匀。从图2、图3和图4中的X=4截面上的总压分布图可以看出，在加油吊舱尾部之后，均出现两个相对低压区，但总压最大值、最小值在截面上中出现的地方不一致，k-ω湍流模型的计算结果和其它两种差别较大；在计算域出口X=out截面上，RNG湍流模型和SST湍流模型计算的总压云图还有两个相对低压区，而k-ω湍流模型的计算的总压分布云图只有一个相对低压区，而k-ω湍流模型的计算结果和前两种差别较大。

图2 RNG模型计算的总压图

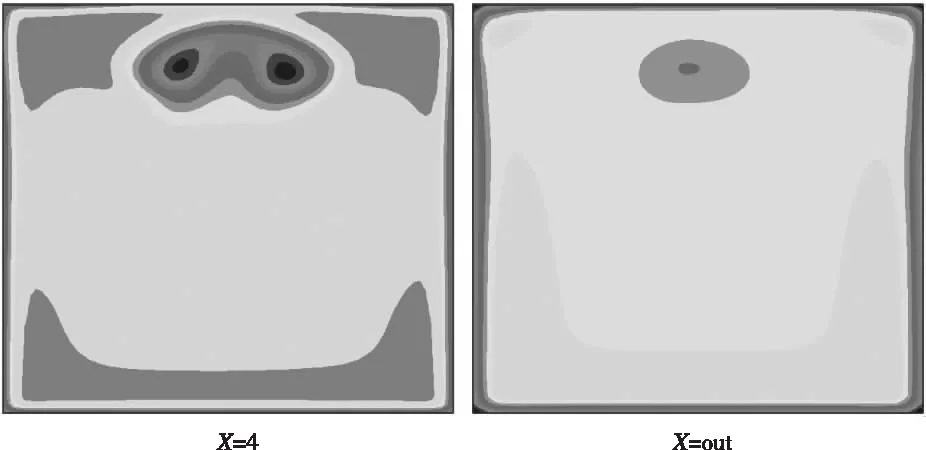
图3 k-ω模型计算的总压图

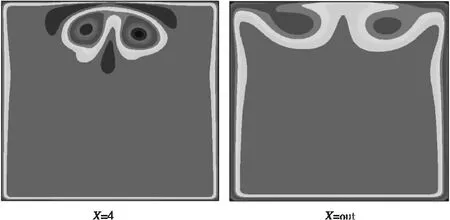
图4 SST模型计算的总压图

3.2 速度矢量图

图5 RNG模型计算的速度矢量图

以计算域出口X=out截面上的速度矢量图为例对三种湍流模型的计算结果进行对比分析。如图5为RNG湍流模型的计算结果，图6为k-ω湍流模型的计算结果，图7为SST湍流模型的计算结果。从计算结果中可以看出，在计算域出口，k-ω湍流模型的计算结果和其它两种湍流模型计算的结果差别较大，气流的速度矢量呈现无规律性，而图5和图7中，依然存在气流呈对称旋转状。

图6 k-ω模型计算的速度矢量图 图7 SST模型计算的速度矢量图

3.3 涡量分布图

涡是旋涡的一种形态，专指湍流运动中的不均一、不规则的各种尺寸的旋涡[7-9]。涡量，一方面表示流体微团绕曲率中心做整体旋转的角速度，另一方面表示流体微团绕其中心做局部旋转的角速度，旋涡是飞行器绕流中的重要流动现象，对飞行器的空气动力特性有重要影响。涡的尺寸，大的和整个湍流的广延同量级，如在湍流边界层中，最大的涡与边界层厚度同量级；小的则小到分子粘性进行动量交换的尺度。在湍流运动中，由于涡的彼此拉伸机制，使涡由大变为略小、较小、更小的各种尺寸的涡。涡的旋转能量随之由大涡传递给较小的涡，直到最小的那一级涡上粘性应力直接起作用把旋转动能变为热能而耗散掉。

选取X=4 m、6 m、8 m以及计算域出口out截面上的涡量进行对比分析。图8为RNG湍流模型的计算结果，图9为k-ω湍流模型的计算结果，图10为SST湍流模型的计算结果。从图中可以看出，三种湍流模型计算的涡量值随着至吊舱尾部的X方向上距离增大而减小，也就是说加油吊舱的尾涡经历了产生、发展、稳定和耗散过程，尾涡的衰减主要有两个方面的原因，一方面，由于空气有粘性，另一方面，尾涡中相邻两层空气之间存在速度差。因此，影响衰减快慢的因素也就是空气粘性大小和速度差。在同一截面上(如X=4 m)，RNG湍流模型计算的涡量值比SST模型和k-ω湍流模型计算的涡量值大，在接近计算域出口处，k-ω湍流模型计算的涡量分布已经基本一致，也就是说，在此处这种湍流模型计算的气流已经基本混合均匀。

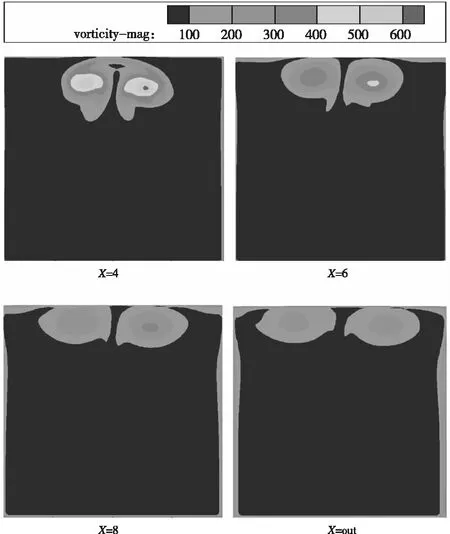
图8 RNG模型计算的涡量图

图9 k-ω模型计算的涡量图

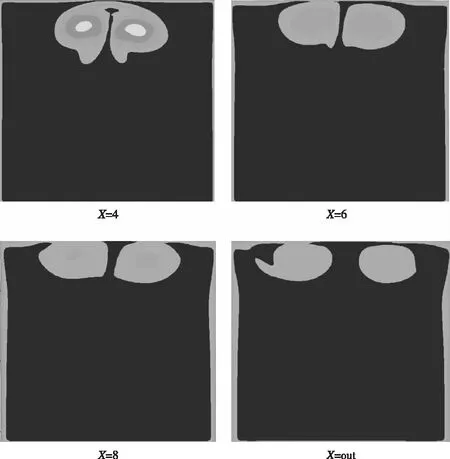
图10 SST模型计算的涡量图

4 空中加油吊舱尾流场试验验证

在进行空中加油过程中，当空中加油软管和锥套回绕至本文所计算的区域内，加油吊舱后尾流场的分布是影响空中加油软管和锥套摆动的重要因素。在进行空中加油飞行试验过程中，在加油吊舱尾部附近和后部加装摄像头，用来观察空中加油软管和锥套的摆动情况。试验表明，当加油软管回绕到本文计算域出口时，锥套的摆动幅度较全拖曳位置时增大，并且有上扬现象，说明在本文计算域出口，加油吊舱后的尾涡并没有完全耗散，从前文给出的三种湍流模型的计算的总压分布图、速度矢量图和涡量分布图中可以看出，在计算域出口，k-ω湍流模型计算结果中的气流已经基本混合均匀，和实际情况差别较大，所以，不适合本文计算域的数值模拟。在空中加油软管和锥套回绕至本文的计算域中时，锥套会与发动机短舱壁面以及飞机机身发生碰撞，并且随着和吊舱尾部距离的缩短，锥套摆动的频率和幅度增大，说明随着和吊舱尾部距离的缩短，加油吊舱尾后流场中涡的强度增大，RNG湍流模型和SST湍流模型的计算结果都符合此规律，只是在同一截面上，RNG湍流模型计算的数值比SST湍流模型的计算数值稍大。

5 结论

本文分别采用RNG湍流模型、SST湍流模型和标准k-ω湍流模型计算某型加油吊舱尾流场的分布情况，将三种湍流模型的计算的总压分布图、速度矢量图和涡量分布图进行对比，通过分析和试验对计算结果进行验证，推荐优先选取RNG湍流模型作为加油吊舱尾流场计算的湍流模型，SST湍流模型次之，标准k-ω湍流模型不适合加油吊舱尾流场计算的湍流模型。