一个圆锥曲线性质的推广
2018-07-30 08:35安徽省合肥市第一中学230601偰永锋
中学数学研究(江西) 2018年7期
安徽省合肥市第一中学 (230601) 偰永锋
文[1]给出了椭圆和双曲线如下共有的性质:
结论4 已知A、B为椭圆E的短轴的两个端点,若过其焦点F的直线AF与椭圆E的另一个交点为C,则直线BC与椭圆E的长轴的交点即为相应准线与长轴的交点.
结论5 已知A、B为椭圆E的短轴的两个端点,其准线与长轴的交点为点M,则过椭圆E的相应焦点的直线AF与直线BM的交点在该椭圆上.
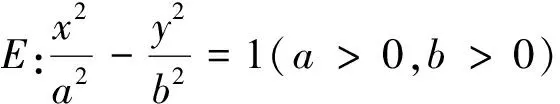
笔者借助几何画板对上面的性质探究时发现对于结论4和5中的A、B不必是短轴顶点,只要是椭圆上关于长轴对称的两点即可,该性质其实是椭圆焦点弦的一个性质,并且这个性质可以推广到双曲线上.对于结论6中的A、B不必是虚轴顶点,只要是虚轴所在直线上关于实轴对称的两点即可.

图1
推广1 如图1,已知A、B为椭圆E上关于长轴对称的两点,点F及直线l为椭圆的焦点及相应的准线,直线AF与椭圆E的另一个交点为C,则直线BC与椭圆E的长轴的交点M即为准线l与长轴的交点.反之也成立.


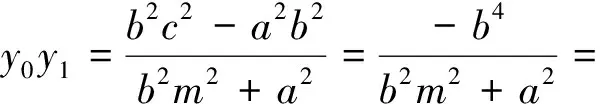
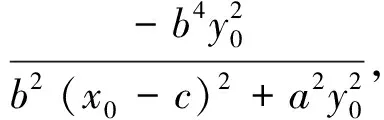

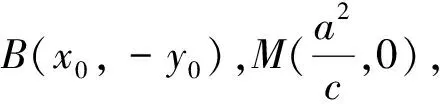

所以直线BC与椭圆E的长轴的交点M即为准线l与长轴的交点.

图2
推广2 如图2,已知A、B为双曲线E上关于实轴对称的两点,点F及直线l为双曲线的焦点及相应的准线,直线AF与双曲线E的另一个交点为C,则直线BC与双曲线E的实轴的交点M即为准线l与实轴的交点.反之也成立.
证明过程与推广1类似,此处从略.

图3
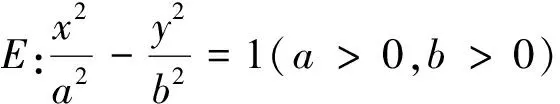
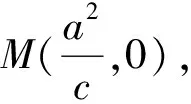
猜你喜欢
中学数学研究(江西)(2022年5期)2022-05-08
装备维修技术(2022年3期)2021-12-06
中学数学研究(广东)(2021年19期)2021-11-19
中学数学研究(江西)(2019年12期)2020-01-10
中学数学研究(江西)(2019年6期)2019-07-08
中学生数理化·教与学(2017年1期)2017-01-19
福建中学数学(2016年7期)2016-12-03
福建中学数学(2013年1期)2013-03-06
中学数学研究(2008年3期)2008-12-09
中学生数理化·高二版(2008年1期)2008-10-19

