启发高中数学学困生学会思考的几点体会*

(410007)

给小学生做问卷调查，评选最喜欢的科目时，数学总是榜上有名.但给高中生做问卷调查，喜欢数学的人的比例就非常低，甚至把数学列为最讨厌的，当然这些学生中大多数是学困生.我对高中数学学困生做了很多次调查，了解他们的情况，其实他们一开始也曾尝过一番努力.做练习的时候，不会做的题目就做两遍，成绩不见起色，就做第三遍，少数学困生，还做第四遍.可是重复做，却迟迟无法进步，他们就会觉得非常沮丧，最后导致对数学厌倦.

如何提高学困生的数学成绩，已经成为高中数学教师的一大难题.当然已经有很多教师在这方面做了很多努力，获得一些好的经验.其实学困生主要是他们的思维和正常学生的思维不同步，比正常学生的思维慢一些，抽象概括能力差一些.教师要想提高学困生的成绩，首先要逐步改善学困生的思维方式，鼓励他们逐步学会思考.为了实现这样的教学目标，就要求教师在数学教学活动中，更多地关心学困生的思维过程，创设合适的教学情境、提出合适的问题，启发学困生独立思考并鼓励他们与其他同学进行有价值的讨论，让学困生在掌握知识技能的同时，感悟数学的思想，积累数学思维的经验，形成良好的思维品质.另一方面，教师也必须要努力去了解他们的困难，尤其是思维方面的困难，有时候要“降低教师自己的思维”去适应学困生的思维；有时候一个非常好的方法不用，硬要去寻找一个繁琐的方法，这个过程对教师来说是痛苦的，但是看到学困生成绩提高时，教师也是非常快乐的.

一、设计倒退的生活情境启发思考

例1 一条铁路线上原有n个车站，为了适应客运的需要，在这条铁路线上又增加了m个车站，客运票增加了62种，求n，m.

反思：通过倒退1950年代的社会情境，使购票环境变得非常简单，引导他离开现代复杂的购票环境，使得他愿意在最近发展区内高兴地思考，从而使学困生顺利求解.数学的教学过程应当给学生创造合理的机会，把课内与课外、知识与生活、理论与实践有机统一起来，给学生的“悟”留有充分的时间和空间；使他们的思维结果在最近发展区内产生.

二、利用转化计算启发思考

例2 20个不加区分的小球放入编号为1，2，3的三个盒子中，要求每个盒内的球数不小于它的编号数，求不同的放法种数.

例2是文[1]中第104页上的一个作业题，只有答案：120种(没有过程).怎么讲解呢？有的教师查找了一些奥赛辅导资料，其中部分奥赛书只有相关定理(没有定理的证明)，文[2]中有定理的证明，但是用“重复组合”知识与方法证明.这些知识与方法对学困生更难以接受，我设计出一个学困生也能接受的情境与方法如下.

反思：这个方法我以前没有想过，因为用奥赛书的结论可以简单解决问题了；这个方法是学困生逼我想的(我还要感谢他们).当x=0这种具体情况出现时，(y,z)的方法种数也就变“简单”了，学困生的胸中也出现了一个看得见的直观方法.所以我们真的应该关注学困生，研究学困生，以学生为本，在观察、研究、反思的道路上会收获属于自己的教育智慧.

三、设计直观的情境启发思考

图1

例3 (2017·高考全国卷丙)如图1，四面体ABCD中，ΔABC是正三角形，AD=CD.

(1)证明：AC⊥BD；

(2)已知ΔACD是直角三角形，AB=BD，若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．

例3的(1)小题取AC的中点O，连接DO，BO，易证.

对于(2)小题，因为在立体几何中很多直观图形不像平面几何图形直观，依次引导学困生画出ΔADC，ΔAEC，ΔBOD，并证明这三个三角形都是等腰直角三角形，每次画好平面图形后都会直观想到：直角三角形斜边上的中线等于斜边的一半；题目难度自然降低.这个题目的难点是在直观图中，学生看不出ΔADC，ΔAEC是等腰直角三角形，更不知道哪个等于90°，所以很多学困生产生误解.

反思：很多时候在立体几何中直观图形不直观.这种情况给很多学生带来了麻烦，有时候给一些学生带来了误导，所以我们教师要千方百计站在学困生的角度去想问题，绝不能一句“这个题简单”.说这几个字容易，但是可能对学困生的自信心是严重的打击.有时候对于真正简单的题，学困生不会做时，我们也可以假装绞尽脑汁在想，使学困生觉得老师做题也是要通过艰苦的努力才能解决的.教师冥思苦想的表情可能对学困生的自信心有意外的提高.

四、合理利用已知数据启发思考

例4 自然数按下表的规律排列，则上起第2007行，左起第2008列的数为( )

A．20072B．20082

C．2006×2007

D．2007×2008

标准答案：选D.经观察可得这个自然数表的排列特点：

①第一列的每个数都是完全平方数，并且恰好等于它所在行数的平方，即第n行的第1个数为n2；②第一行第n个数为(n-1)2+1；③第n行从第1个数至第n个数依次递减1；④第n列从第1个数至第n个数依次递增1.故上起第2007行，左起第2008列的数，应是第2008列的第2007个数，即为[(2008-1)2+1]+2006=2007×2008.

以上标准答案对学困生来讲是较难的，注意到要求解的数是上起第2007行，左起第2008列，我引导一个学困生先观察第1行第2列的数，再观察第2行第3列的数，再观察第3行第4列的数，再观察第4行第5列的数，他很快通过类比选对了答案，他的那种成功的快乐感立即洋溢在脸上，因为他比尖子学生还先做对题目.

反思：小题小做已经成为解决选择题的一种好方法，这种方法的基础也是有“根据”的类比思维，以事实、数据和已经得到证实的知识作为依据进行推理和思维.对学困生更应该鼓励他们去实践，去寻找题目的某些特点，然后启发他们归纳和概括，让他们在解题的过程中找到成功的喜悦，从而使他们逐步树立学好数学的信心.

五、设计阅读的环节启发思考

例5 如图2，已知V是ΔABC外一点，VB⊥平面ABC，平面VAB⊥平面VAC．求证AC⊥AB．

对于例5，学困生一般从整体上感受，这个结论是显然的，就是不知道从哪里开始写？怎样写？实在要他写，他就绕着圈子乱写；主要表现是逻辑混乱、杂乱无章，教师追问他，他就说：老师我写的哪一句话不成立吗？当然他写的每一句话从图形的本质来看都是对的，他把一些正确的事实用混乱逻辑连在一起；他用前后颠倒的顺序把一些结果连在一起.对于这种情况，我先不评价他，要他先把课本中的定理阅读几遍：

图2

定理[3]两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直.

一直等他对以上定理很熟练时，再问他怎样理解这个定理，要应用这个定理，必须有什么线线垂直作基础？此时他想到要先找两个平面的交线VA，再通过点B作BD⊥VA交VA于D，然后证明BD⊥平面VAC.最后顺利证明该题.

反思：阅读是看书，但不是一般意义上的浏览，看书领会其内容才是阅读，领会定理内容意味着把看到的东西纳入已有的知识和经验中去，使其连成一体.这个题中的辅助线，不能通过教师直接灌输使学困生掌握，而是要引导他们多次阅读课本，让他们在阅读的过程中，理解→想象→分析→推理→判断→创意→自我理论化→解决问题.

六、对常规问题猜想启发思考

例6 (2015·高考全国卷Ⅱ)已知函f(x)=lnx+a(1-x)．

(1)讨论f(x)的单调性；

(2)当f(x)有最大值，且最大值大于2a-2时，求a的取值范围．

分析：大多数情况下，猜想教学是在开放性问题或探究性问题中进行的，在常规问题中很少进行猜想教学.近几年的全国卷高考数学试题在引导鼓励学生进行猜想方面做了很多很好的努力，这是全国卷匠心独运的地方.例6的(2)小题是常规问题，用常规思维求解，难度增加，因为其中需要求解方程lna+a-1=0，不等式lna+a-1>0，和不等式lna+a-1<0，求解这三个方程和不等式是难点，怎样突破这个难点？这就需要猜想探路.超越方程一般没有解析解，而只有数值解或近似解，只有特殊的超越方程才可以求出解析解来.对于这个超越方程鼓励学生从数学审美的角度去想问题，自然猜想a=1时lna+a-1=0.这个猜想对于平时训练有素的学生不难，对于平时没有训练的学生可能无法继续求解.

反思：著名数学家G.波利亚强调数学教师不仅要教学生证明，而且要教学生猜想.所以在数学教学中，教师应该把"引导学生进行猜想"作为一种教学手段，引导学生在各种情境下持之以恒地观察现象，研究问题，形成猜想，促使学生积极参与学习的全过程，主动地获取知识.教师应根据不同的教学内容，抓住不同的时机，创设猜想的情景，让学生去大胆猜想.在猜想教学过程中，不同层次的学生都会有不同的收获，学困生也可以在特殊情况的求解过程中获得成就感，增强自信心，尖子生可以继续拓展、延伸与推广.

先猜想，后证明，这是数学发现的思路，也是最见数学功力的，对于例6、7要求学生有“猜想”的自觉性.对一个真正的问题我们可以说结果是算出来的，是证出来的，因为算和证是终结性表达，是必须履行的手续.但履行手续前是需要实质性工作的，这个实质性工作就是猜想.

七、建构几何模型启发思考

图3

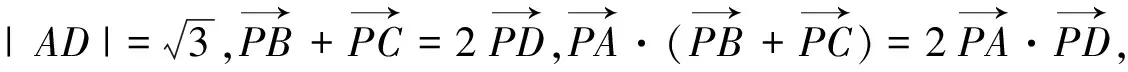
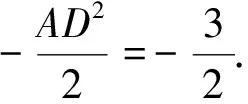
反思：本题利用平面几何知识，构造几何模型来解决向量问题，淡化繁杂的代数计算，淡化非数学本质的纯粹说明，使“向量”变得容易些.笛卡尔说，没有任何东西比几何图形更容易印入脑际了，因此用几何这种方式来表达事物是非常有益的.人们在学习数学时需要不断的经历直观感知、观察发现、归纳类比等思维过程.从心理学的角度看，数学教学需要一些直观性的设计，作为学生理解抽象数学结论的现实基础，作为学生主动建构、发现新知识的认知基础，作为学生探究性学习的基础.

八、设计活动启发思考

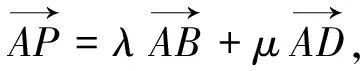
这个题是选择题中的压轴题，文[4]的解答方法是，先建立适当的平面直角坐标系，再求圆的方程，然后利用圆的参数方程和三角函数中的辅助角公式，最后求出λ+μ的最大值.这个方法较复杂，其书写的文字比解答题的第17题还多很多(此处从略).而且没有学习过参数方程的高一和高二好学生看不懂，学困生更看不懂.有没有简单的方法呢，有没有学困生也能理解的方法呢？我设计了一个有关的活动，使学困生也能简单解答此题.

图4

图5

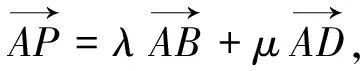
更为可喜的是部分学生(包括一些学困生)继续思考得到了如下一些结论，不同层次的学生获得了不同程度的提高.

反思：本次活动主要材料纸中的一些等距离平行线，给每个操作者有利的刺激，给学困生也提供了强有力的情境.这些平行线不断的激发他们的感觉和思维，使他们有意或无意的联系题目，真的让他们联想不断，尤其是这次活动中的计算量不大，只要直觉思考，就可以整体把握问题的本质特征；使得平时计算能力不好的学困生也可以扬长避短，获得成功的喜悦.这次活动使每一个学生都能深入学习过程中，深入知识的形成过程、转化过程中.在活动中理解了知识所蕴含的思想和智慧；随着活动的深入，他们敢于质疑，表现出不唯书、不唯师，不满足于现成的答案和说明.在这次活动中，他们感觉到自己的智慧和力量，体验到创新学习的快乐.在活动中他们也获得了积极的情感体验.作为教师要努力寻找这样的既经济又高效的活动，要千方百计去开发一些直观易懂的有利于学困生的活动.

总之，笔者感觉高中数学对某些学生来说有一定难度，但是笔者愿意引导学困生在克服困难中努力前进，在克服困难中增长才干，培养坚强的意志力，在克服困难中提高思考能力.当然这是一个富有魅力又充满挑战的课题，很希望各位同仁批评指正.