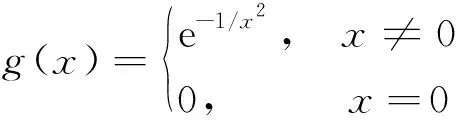两条水平射线的光滑连接*
石冶郝 伍和用
(1.首都师范大学初等教育学院, 北京 100048; 2.湖南省新邵县寸石镇大富学校 湖南 新邵 422907)
0 引 言
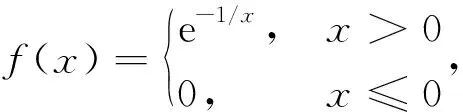
文[2]用五种不同的方法得出函数e1/x的高阶导数公式:
(*)

0≤φ(x)≤1,∀x∈R;
φ(x)=1,x≥1;φ(x)=0,x≤0.
0≤ψ(x)≤1,∀x∈R;
ψ(x)=1,x≥b;ψ(x)=0,x≤a.
例如
在R上可导任意多次,而且它的图象中段隆起,两侧水平展开,将这样的函数称为钟形函数或隆起函数(bump function).
在一些实际应用中,如果需要光滑连接两条水平射线,这里光滑意指无穷次求导.由泛函分析的知识,这样的函数是存在的(见[3,定理1.1.5]),而且由卷积的形式给出.本文从函数e1/x出发,构造一个分段函数属于C∞(R),实现两条水平射线的光滑连接.
1 主要结论
定理设a 这里c1,c2为常数,exp(x)=ex,则F(x)∈C∞(R). 证明设函数 现在只须证明函数H(x)∈C∞(R).显然函数H(x)在x≠0,x≠-1处可以无穷次求导,只须考察它在x=0,x=-1处的可导性. 接下来我们证明函数H(x)的高阶导数H(n)(x)满足 h′(x)=h(x)e1/x[(x+1)-2+(x+1)-1x-2], 继续求导,由乘积函数的高阶求导法则与引言中的(*)式,计算得h(r)(x)为形如 的函数之和,其中c(x)是1/x的多项式,在x=-1连续,i,j,k为正整数. 当-1 因此H(n)(x)为形如 的函数之和,其中c1(x)是1/x的多项式,在x=-1连续,c2(x)是1/(x+1)的多项式,在x=0连续,i1,j1,k1,k2为正整数.而对任意的正整数k,根据洛比达法则,有 于是, 函数H(x)的图象如下: 同理函数H(x)在x=0处的泰勒级数 在实轴上收敛,且和函数恒等于零,它不等于H(x).因此研究某个函数的泰勒级数时,必须讨论这个级数的余项.
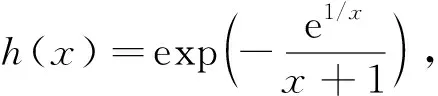

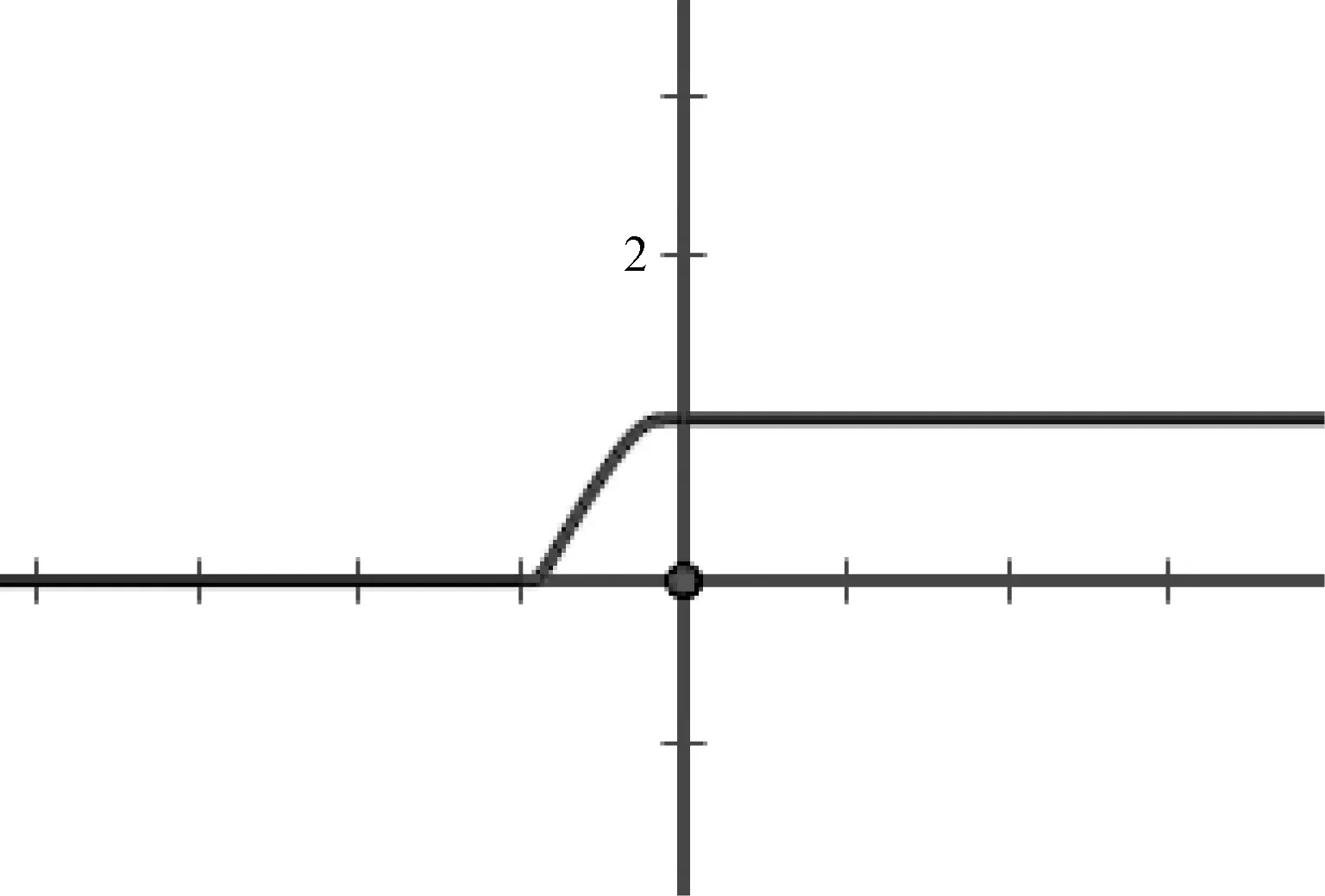
2 说 明