基于高光谱影像的SG滤波算法的研究

何英杰 谢东海 钟若飞

(首都师范大学资源环境与旅游学院， 北京 100048)

0 引 言

经历全色到多光谱扫描仪成像阶段之后，在20世纪80年代初由于成像光谱概念的出现，遥感技术进入了高光谱遥感的崭新的阶段.高光谱遥感是当前遥感的前沿技术之一，是将成像技术和光谱技术相结合的多维信息获取的技术.它是由多光谱遥感成像技术的基础发展而来的，光谱分辨率得到了大幅的提高[1]，为每个像元提供几乎连续的地物光谱曲线,使我们利用高光谱反演陆地细节成为可能[2].

获取较高的光谱分辨率的连续的图像数据是高光谱遥感数据的闪耀之处,它能充分地反映地物反射率光谱的细微特征.然而，高光谱图像成像仪器以及环境等因素对数据获取造成的影响，使得在高光谱数据成像和预处理的各个环节中，都可能引入不同程度的噪声，高光谱图像具有空间图像和地物光谱两个方面的信息，因而噪声对高光谱图像的影响最终也会表现为空间域噪声和光谱域噪声两方面[3]，严重地限制了高光谱数据的高光谱分辨率的优势.

人们根据实际图像的特点、噪声的统计特征和频谱分析的规律，发展了各式各样的去噪方法.其中最直观的方法是根据噪声能量一般集中于高频，而图像频谱分布于一个有限区间的这一特点，采用低通滤波方法.在基于三角网格模型的降噪算法研究方面，Yu等[4]提出一种两阶段特征保持网格去噪框架.此外，对图像进行平滑处理也是常用的方法.平滑的目的有两个：改善图像质量和抽出对象特征.一个较好的平滑方法应该既可以消掉噪声影响又不使图像的边缘轮廓和线条变模糊.刘倩[5]基于非局部稀疏的图像处理方法，充分利用自然图像本身的有用信息，有效弥补了数学模型的缺陷，以数据驱动的方式大大提高了图像平滑的效果.图像平滑处理方法有空间域处理和频率域处理两大类.在空间域里一类方法是噪声去除，即先判定某点是否为噪声点，若是，重新赋值，若不是按原值输出；另一类是平均，即不依赖于噪声点的识别和去除，而对整个图像进行平均运算.而在频率域里是对图像频谱进行修正，一般采用低通滤波方法，而不像在空间域里直接对图像像素灰度级值进行运算.图像的均值滤波模板和中值滤波模板是实现图像的平滑去噪的主要方法.

由于高光谱图像成像时自然光照明条件影响、地面地形影响、混合像元问题等原因引入各种噪声，这些噪声存在于光谱域中，同样也是需要检测并予以去除的[6].MNF(minimum noise fraction)变换通过降低数据的维数来达到隔离数据噪声的目的，首先使用噪声的协方差矩阵分解并将数据中的噪声白化[7],此时噪声具有单位方差，并且与原波段无相关性.然后针对上述噪声白化的数据进行标准的主成分变换；Boardman[8]针对这个问题提出了EFFORT方法，即通过统计高光谱图像，寻找一种微调来减小误差，从而提高反射率的精度；Gladden[9]同样认为反射率转换后光谱中会产生很大的噪声，并采用一种 SSE线性校正方法，即将转换后反射率光谱拟合到实测地物光谱上，达到去除噪声的目的.陈志刚和束炯[10]基于光谱二阶导数检测噪声的基础上，提出了基于经验模态分解EMDF(empirical mode decomposition based filter)的光谱域滤波方法及其修正，具有较好的光谱域滤波效果.由于多分辨率的分析特性和较好的时频局部化，小波分析[11]依据小波基函数，多层次地分解高光谱图像光谱.然后针对分解后的小波系数选取合适的阈值进行处理，最终获得滤除噪声后的光谱曲线，在图像处理领域得到广泛应用.杨浩等[12]针对成像光谱仪采集的高光谱图像数据，提出一种小波阈值去噪方法去降低噪声影响.遥感影像存在的光谱锯齿噪声[13]，同样也严重影响矿物光谱吸收参数的提取.

Savitzky和Golay[14]提出的最小二乘滤波算法，滤波器的选择为Savitzky-Golay(SG) 滤波器，它是一种特殊的低通滤波器，最初由Savitzky和Golay于1964年提出.光谱曲线由于受各种噪声的影响而呈现锯齿状，经SG滤波处理后，平滑一些细微的锯齿噪声同时能保持整条曲线大的光谱特征不受影响[15-16].本文主要以航空高光谱遥感数据为研究对象，在SG滤波器的基础之上进行优化，求取反射率光谱的二阶导数，以期使其能更加灵活且准确地处理影像.

1 高光谱影像SG滤波法分析

在平面坐标系中,用一条曲线来拟合一组数据,不妨假设这条曲线为y=a0+a1x+a2x2+a3x3+a4x4，当每一个点的横坐标代入这个曲线方程后，所得值与该点的纵坐标之差的平方之和最小时，这条曲线的拟合度最高，从而可以确定所有的系数ai(i=0,1,2,3,4).

从高光谱影像中每个像元提取出的反射率曲线本身有一定的物理意义，可以反映地物的细微特征，但是转换后的像素光谱反射率曲线的噪声一般呈锯齿状分布，这些锯齿分布即为高光谱图像光谱域噪声，严重地限制了其高光谱分辨率的优势.为了去除光谱域噪声，考虑采用多项式拟合的最小二乘平滑算法，剔除一些细微的锯齿噪声同时能保持整条曲线大的光谱特征不受影响.SG滤波法[14]是一种经典的最小二乘平滑算法，它使用简化的最小二乘拟合卷积方法对曲线进行平滑处理并可计算平滑后曲线的各阶导数.

扩展一下，通常假设曲线为p次多项式，即满足公式(1)

Yi=a0+a1i+a2i2+…+apip

(1)

其中，Yi第i点平滑后的数值.

用上述多项式拟合曲线的误差可以表示为：见公式(2)

(2)

其中，yj代表平滑前的数值，平滑窗口大小k=2m+1.为了让误差S最小，需要对S进行偏微分，使得所求S偏微分各项为零.因此，可以得到以下各式：关系如公式(3)

…

(3)

Savitzky对整个求解过程进行了推导，给出了平滑窗中心点平滑后数值的最后公式及公式中系数的计算方法[14].Madden[17]基于Savitzky的计算公式，改正了原SG系数的一些错误，并且给出了各阶导数平滑系数修正后的计算公式.根据其推导平滑后的曲线数值的最小二乘卷积方程可写为：见公式(4)

(4)

(5)

式中，m为平滑窗宽度的一半[18].

SG滤波器有如下几大优点[19]：

1)利用最小二乘的多项式拟合方法非常清晰易懂，并且在计算上来说，多项式卷积的操作比最小二乘的计算可操作性更强；

2)滤波系数只需要在对应的卷积系数表中进行查找，很容易获得；

3)SG滤波器可以有任意的长度，因此有利于采样频率通常很低的生物学或者生物力学的数据处理.

SG算法的本质是一种最小二乘法的卷积平滑，根据多项式拟合阶数和平滑次数进行综合考量，但是多项式拟合曲线的误差求取的是一阶导数.本文高光谱影像噪声检测SG算法是基于光谱二阶导数.光谱导数技术对光谱信噪比非常敏感，光谱的一阶、二阶导数计算公式如下[20-21]：

(6)

(7)

其中，近似选取相邻两点，其关系满足公式(8)

Δλ=λk-λj=λj-λi,λk>λj>λi

(8)

光谱的低阶导数处理对噪声影响敏感性较低，而高阶微分对噪声影响敏感度高.相比较一阶导数，二阶导数很好的反映了噪声的实际分布情况(高阶导数过于复杂).因此，可以考虑用光谱二阶导数对光谱曲线进行噪声影响程度检测.

对于光谱曲线进行光谱二阶导数计算，考虑将其与平均值进行相减，然后一般想法是参考差值分布，与一个固定的值进行比较，即设定一个阈值，判定噪声与否.然后根据SG滤波法通过对反射率光谱二阶导数的统计，得到光谱各波段中噪声的判定函数，在噪声较严重的波段进行较多点数的SG滤波，对噪声不太严重的波段进行较少点数的SG滤波，从而确定该波段滤波平滑窗的大小.根据计算表明，如果判别式满足公式(9):

(9)

那么该波段反射率的值认为是有较大噪声的存在，其中σ表示光谱二阶导数的标准差.

在噪声检测完成后，可以先采取较大窗口的SG滤波对较大噪声波段进行局部第一次平滑，其他波段保持不变，得到初步的滤波结果；然后采取较小窗口的SG滤波对初次滤波的结果进行光谱曲线的整体平滑.这样的好处是，既可以对光谱曲线进行平滑滤波和噪声去除，又可以最大程度的对光谱细节进行保留.

本算法的具体步骤如下：

1)从高光谱图像中逐像元的提取光谱特征，绘制反射率曲线；

2)计算曲线的二阶导数；

3)计算光谱二阶导数的均值与方差，按照公式(9)判定噪声；

4)进行第一次平滑，对判定为噪声的波段进行例如11点SG滤波平滑，保持其他波段不变；

5)进行第二次平滑，对第一次平滑后的光谱曲线进行例如5点(一般选择小窗口的值为大窗口值的一半取整)的SG平滑;

6)该点处理完毕，转入下一像素点的处理，转入步骤2，直到所有点处理完毕.

2 实验验证与分析

2.1 影像数据选择

试验数据为2012年武汉市某地区PHI高光谱遥感影像，包含80个波段，光谱范围400～850 nm，大小为128行、128列.选取比较有代表性的波段进行展示，例如49、51、53波段，如图1所示.

图1 49、51、53波段影像

图像质量评价的研究是图像信息学科的基础研究之一.对图像处理或图像通信系统，其信息的主体是图像，衡量这个系统的重要指标，就是图像的质量，而图像去噪就是为了改变图像的主观视觉显示图像质量[22].我们需要考虑的几个因素总结如下：1)去噪后图像应尽量的平滑，不存在或有较少的噪声痕迹.2)去噪结果不能使图像过渡的失去结构细节而变得模糊.3)没有由于具体去噪方法产生的人工噪声.4)均方差尽可能小.所有这些都要求有一个合理的图像质量评价方法.根据图像质量评价方法的思想，初步对所给数据进行分析：波段存在划痕状条带噪声，以及分布不均匀的随机噪声，以49波段噪声特点较为明显.根据光谱域处理噪声的结果与一般平滑去噪的不同，要尽量保证噪声点附近平滑处理，而不影响非噪声点光谱特性.基于高光谱影像应用SG滤波算法，可以满足预期设想.

2.2 结果分析

根据已经设计好的实验步骤，编写程序并在matlab环境下运行，3个波段原始图像、噪声分布图以及去噪后的对比图像展示如图2所示.显然，如果噪声分布不是明显的划痕式或者条带式分布，那么很难直观地对比去噪前后影像的差异.因此，提取算法输出横轴为波段数，纵轴为亮度信息的曲线(如图3(b)、图4(b)、图5(b)所示)，曲线上每一点代表相同点在不同波段上的亮度表达，从曲线走势上可以清楚看出滤波前后差别.

选取第53波段中一点(39,7)如图3，为第39行第7列的数据点，十字叉丝代表选点，下同.

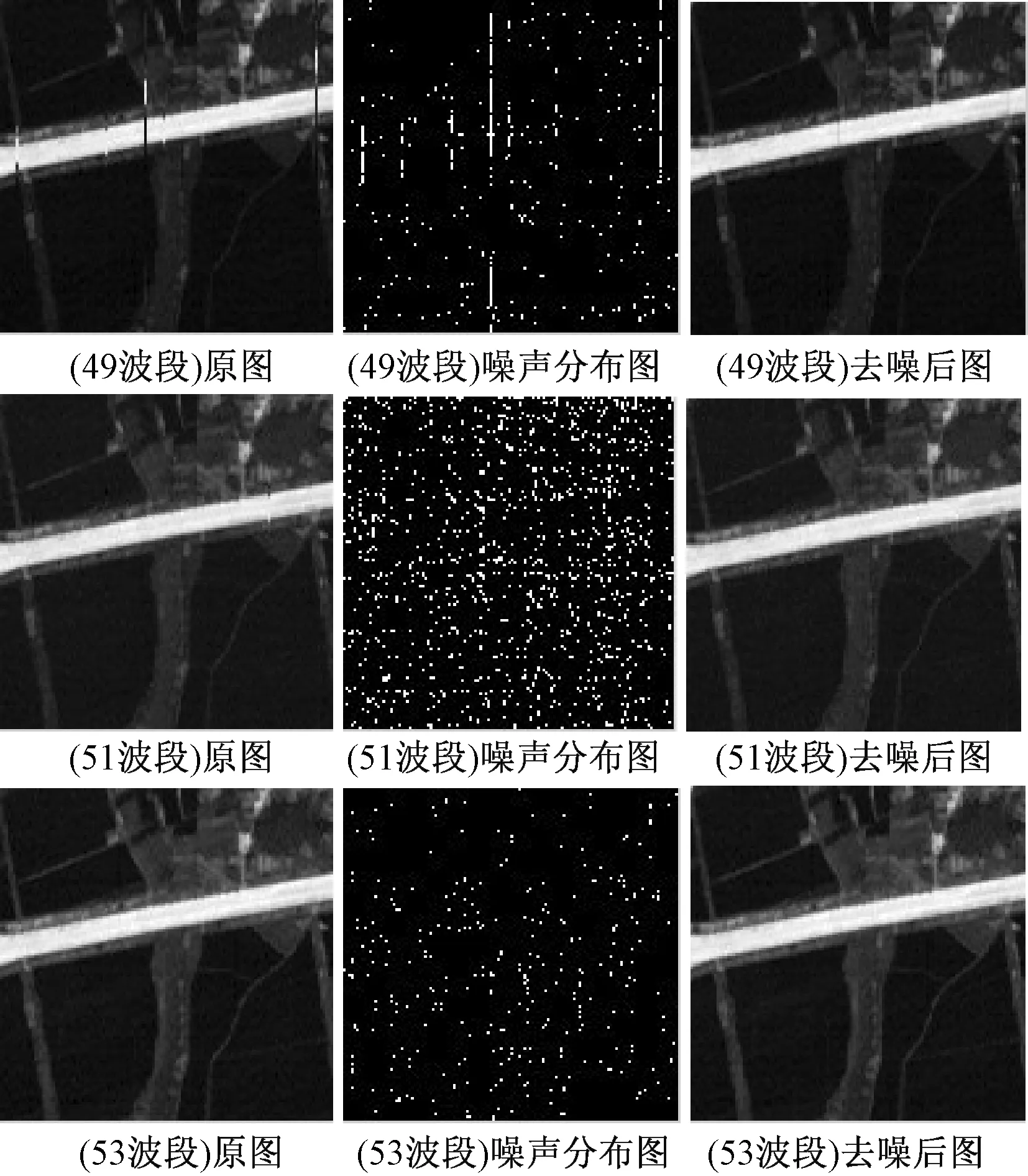
图2 滤波前后对比以及噪声分布图

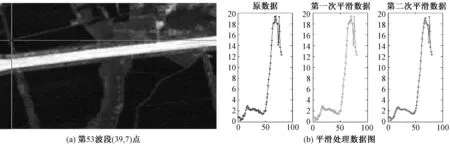
图3 第53波段处理示例

图4 第49波段处理示例

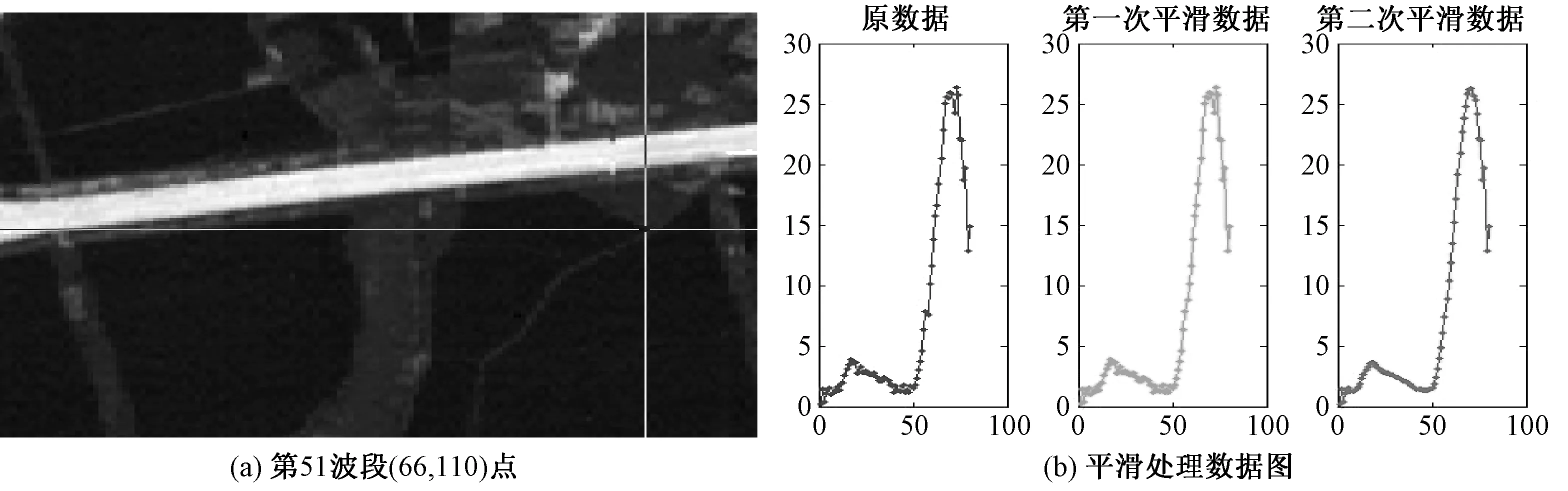
图5 第51波段处理示例

如图3所示，前50波段曲线走势变得平滑，但是由于波段窗口的选择(此次实验选取的大波段值为11)，后面几个数据没有得到较好的处理，这是算法的不足之处；还有一种情况就是数据本身的原因，没有滤掉噪声.

图4和图5为第49波段和第51波段平滑处理后可以较好地保留图像信息，曲线走势保留较好，图像信息较为完整.

从图3(b)、图4(b)、图5(b)可以看出，算法对于高光谱图像的最大作用体现在最大程度地保留曲线走势；由于反射率变换后的图像光谱曲线受各种噪声影响而成锯齿状，经过处理以后图像光谱平滑了许多(从示例平滑数据图像中可以明显看出)；同时保持了一些如吸收峰等细微的光谱特征.

2.3 精度评价

为了与高光谱其他的去噪方法比较，应用相似函数[23]：1)光谱角度距离：夹角越小，光谱间相似度越大；2)光谱欧几里得距离：距离值越小，两光谱越相似；3)光谱相关系数：光谱间相关系与光谱相似度成正比，完全相似的光谱间的相关系数为1.通过计算得到如表1.

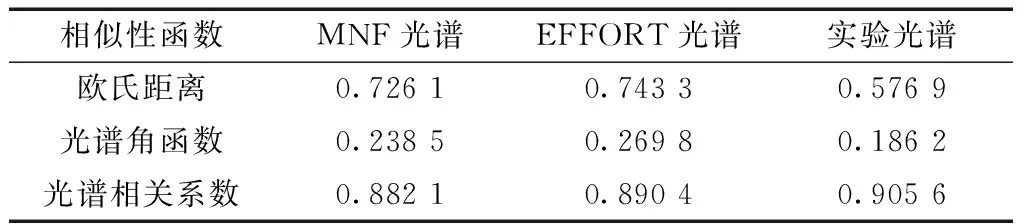
表1 三种方法处理后的相似函数

MNF变换通过降低数据的维数来达到隔离数据噪声的目的，EFFORT方法通过统计高光谱图像，寻找一种微调来减小误差，从而提高反射率的精度.二者都是光谱域滤波的经典算法，但是由于计算量和阈值的选取，本文的算法无需降维，阈值选取也较为简单，在运算效率方面有所改观.由表1计算结果看，相似度越大，表明在最大程度上保留了原光谱的信息，因此在保证去除高光谱图像中的噪声的同时，相似度的判定可以比较算法的改进.基于光谱二阶导数的实验滤波方法都要优于其他两种方法，与实测光谱更加接近，滤波效果更佳.

3 结 论

根据光谱特征，基于高光谱影像提出一种利用光谱曲线二阶导数的SG滤波去除噪声的算法，得出以下结论：

1)基于光谱二阶导数的滤波算法能最大程度保留曲线走势，有效地去除光谱域噪声，保留光谱原有的大部分光谱特征，是高光谱图像预处理的一种简单且有效的手段.

2)相比较其他算法，本文采用的算法花费的时间也较少，相似性函数反映滤波后光谱与实测光谱相似度最大.

当然，算法也存在着不足.实验算法存在着边界效应，针对两端波段不能进行较好的处理；实验仅对比了实测光谱(含噪声)和滤波后光谱，并未在此基础上添加不同类型噪声，因此在适用性方面还有所欠缺.